Алгебра высказываний

«Память становится мыслящей»
(Д.Б.Эльконин)

Формы мышления и история развития
алгебры логики
История логики насчитывает около двух с половиной тысячелетий. Первые учения о формах и способах мышления возникли в Древнем Китае и Индии. Основоположником формальной логики является Аристотель (384-322 гг. до н.э.) – древнегреческий философ, который впервые отделил логические формы мышления от его содержания.
Алгебра логики – наука об операциях, аналогичных математическим, над высказываниями или над объектами, которые могут принимать только два значения – «ИСТИНА» или «ЛОЖЬ».
В 1842 году английский математик Джорж Буль разработал математическую логику или алгебру логики, которую впоследствии стали называть «булевой алгеброй».
Спустя 100 лет алгебра логики стала основой теории цифровых вычислительных машин, ее используют в компьютерной логике, электронике, в основе всех микропроцессорных операций.

Формы мышления и история развития
алгебры логики
Многие философы и математики развивали отдельные положения логики и иногда даже намечали контуры современного исчисления высказываний, но ближе всех к созданию математической логики подошел уже во второй половине XVII века выдающийся немецкий ученый Готфрид Вильгельм Лейбниц (1646— 1716), указавший пути для перевода логики “из словесного царства, полного неопределенностей, в царство математики, где отношения между объектами или высказываниями определяются совершенно точно”. Лейбниц надеялся даже, что в будущем философы, вместо того чтобы бесплодно спорить, станут брать бумагу и вычислять, кто из них прав. При этом в своих работах Лейбниц затрагивал и двоичную систему счисления.
Уже в XIX веке стало понятно, что система Буля хорошо подходит для описания электрических переключательных схем. Ток в цепи может либо протекать, либо отсутствовать, подобно тому, как утверждение может быть либо истинным, либо ложным. А еще несколько десятилетий спустя, уже в XX столетии, ученые объединили созданный Джорджем Булем математический аппарат с двоичной системой счисления, заложив тем самым основы для разработки цифрового электронного компьютера.

Логика, как наука развивается с IV в. до н. э. начиная с трудов Аристотеля. Именно он подверг анализу человеческое мышление, такие его формы, как понятие, суждение, умозаключение.
Логика (от греч. “логос”, означающего “слово” и “смысл”) – наука о законах, формах и операциях правильного мышления.
Ее основная задача заключается в нахождении и систематизации правильных способов рассуждения.

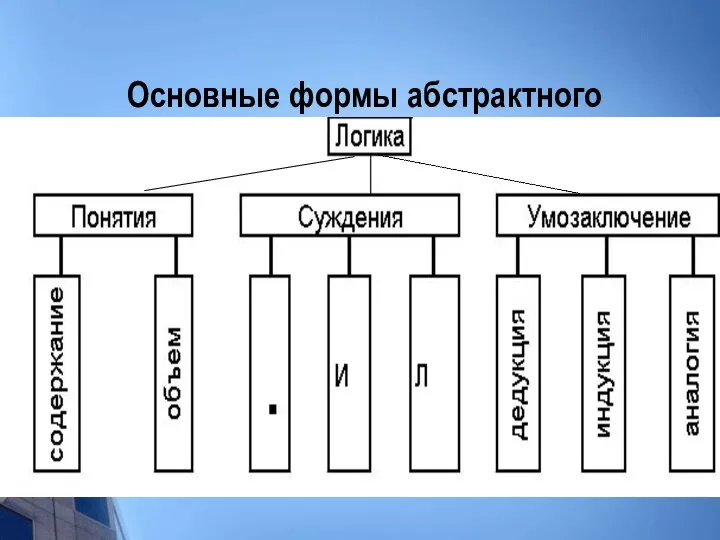
Основные формы абстрактного мышления

Понятие – это форма мышления, в которой отражаются существенные признаки отдельного предмета или класса однородных предметов. Всякое понятие имеет содержание и объем
Например, понятие “Черное море” – отражает единичный предмет, “Сиамская кошка” – отражает класс сиамских кошек.
Содержание понятия – совокупность существенных признаков множества, отраженных в этом понятии.
Например, понятие “квадрат” – прямоугольник, который имеет равные стороны.
Объем понятия – множество предметов, которые мыслятся в понятии.
Например, под объемом понятия “лев” подразумевается множество всех львов, которые существовали, существуют и будут существовать.

Высказывание (суждение) – повествовательное предложение, о котором можно сказать истинно оно или ложно.
Бывают простые и сложные (объединяют несколько простых).

Примеры высказываний
Истинное высказывание: «Буква «А» - гласная».
Ложное высказывание: «Компьютер был изобретен в середине XIX века».
Какие из предложений являются высказываниями? Какие из высказываний истинные?
1. Какой длины эта лента?
2. Прослушайте сообщение.
3. Делайте утреннюю зарядку!
4. Назовите устройства ввода информации.
5. Кто отсутствует?
6. Париж – столица Англии.
7. Число 11 является простым.
8. 4+5=10
9. Без труда не вытащишь и рыбку из пруда.
10. Сложите числа 2 и 5.
11. Некоторые медведи живут на Севере.
12. Все медведи – бурые.
13. Чему равно расстояние от Москвы до Ленинграда?
14. Сумма углов треугольника – 180 градусов.

№1. Какие предложения являются высказываниями?
Москва – столица РФ.
Алуштинский дворец (Ласточкино гнездо) находится в Крыму.
5 – 9 + 8.
5 – 9 + 8 = 4.
На юге Африки живут пингвины.

№2. Определите, какие из следующих предложений являются высказываниями, а какие нет. Какие из высказываний истинные, а какие нет?
Учить второй иностранный язык легче, чем первый.
Обязательно займись каким-либо видом спорта.
Переводчик должен знать хотя бы два языка.
Ты играешь в хоккей?
Отними от неизвестного числа 5 – и получишь 2.
К концу 11 класса хорошо выучу русский язык.

Умозаключение – это такая форма мышления посредством которой из одного или нескольких суждений с необходимостью выводится новое заключение о предметах реального мира.
Умозаключения бывают:
Дедуктивные (от общего к частному) – Все ученики ходят в школу. Вася – ученик. Вася ходит в школу.
Индуктивные (от частного к общему) – Банан и персик – сладкие. Значит, все фрукты сладкие на вкус.
Аналогия – Наши коровы едят траву и дают молоко. В Австралии есть поля, коровы едят эту траву. Следовательно, австралийские коровы тоже дают молоко.

1. ВСЕ АНТИЛОПЫ СТРОЙНЫЕ.
2. СТРОЙНЫЕ ЖИВОТНЫЕ РАДУЮТ ГЛАЗ.
ВСЕ __ ______ РАДУЮТ ГЛАЗ.

1. ВСЕ АНТИЛОПЫ СТРОЙНЫЕ.
2. СТРОЙНЫЕ ЖИВОТНЫЕ РАДУЮТ ГЛАЗ.
ВСЕ _АНТИЛОПЫ_ РАДУЮТ ГЛАЗ.

Логические величины – это понятия выражаемые словами Истина или Ложь.
Логическая переменная – это символически выраженная логическая величина.
Логическое выражение – это простое или сложное высказывание о котором можно сказать Истинно оно или Ложно.

Формы мышления

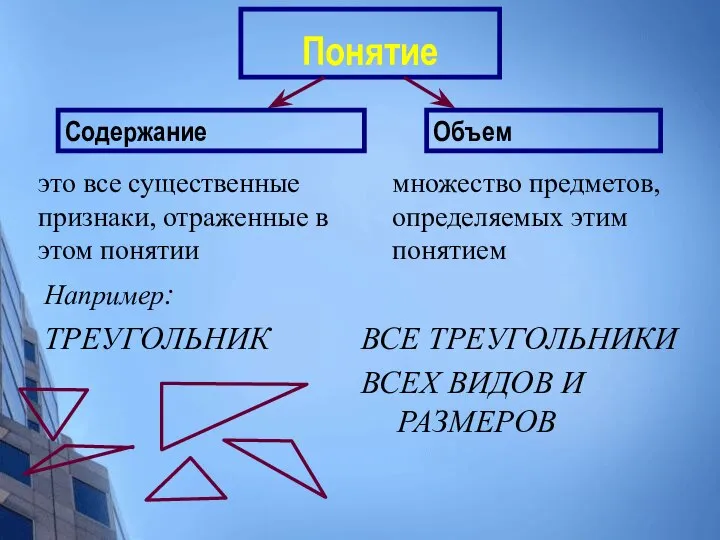
Понятие
это все существенные признаки, отраженные в этом понятии
множество предметов, определяемых этим понятием
Например:
ТРЕУГОЛЬНИК
ВСЕ ТРЕУГОЛЬНИКИ
ВСЕХ ВИДОВ И РАЗМЕРОВ

Объем растет
Содержание
уменьшается
Объем уменьшается
Содержание растет

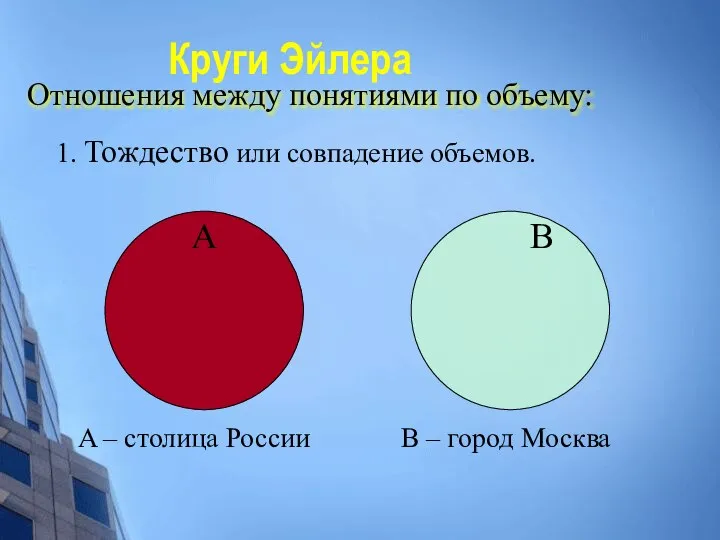
Круги Эйлера
А
B
A – столица России
B – город Москва
Отношения между понятиями по объему:
1. Тождество или совпадение объемов.

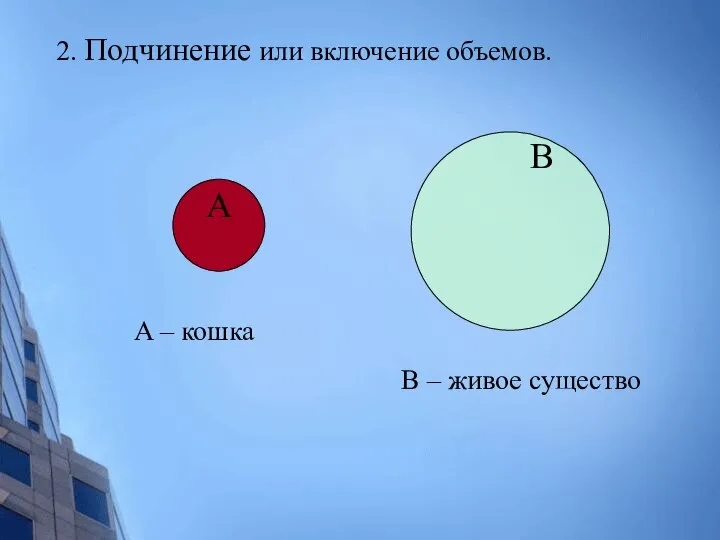
B
A – кошка
B – живое существо
2. Подчинение или включение объемов.
А

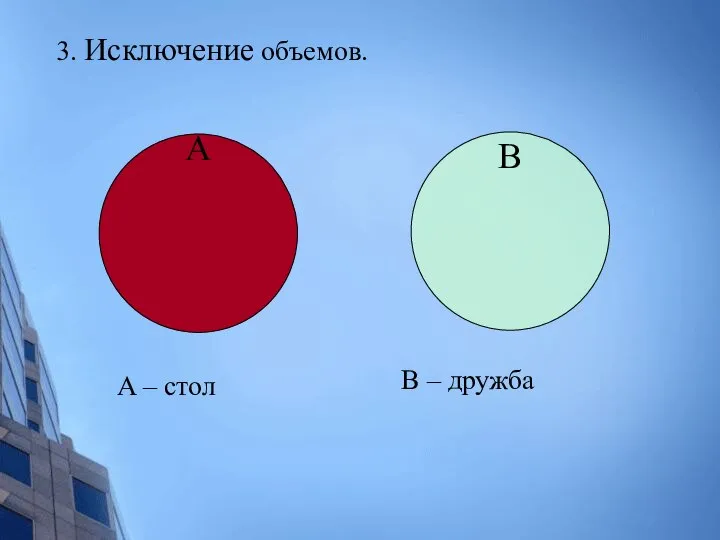
B
A – стол
B – дружба
3. Исключение объемов.
А

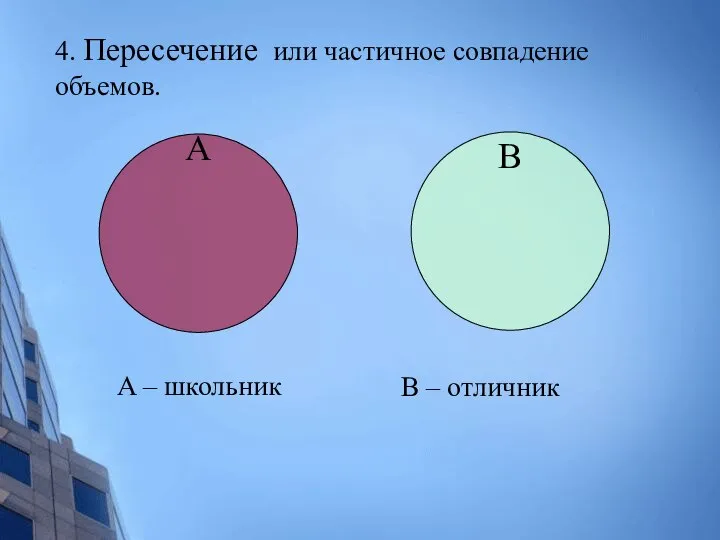
B
A – школьник
B – отличник
4. Пересечение или частичное совпадение объемов.
А

Логические операции

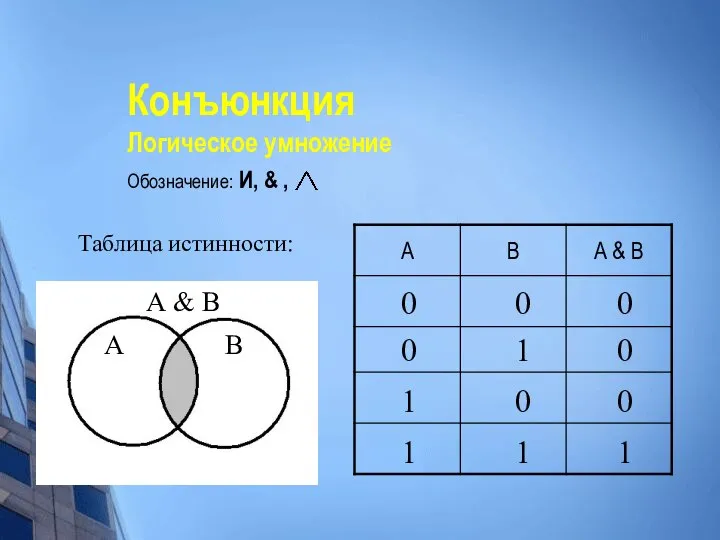
Конъюнкция
Логическое умножение
Обозначение: И, & ,
Таблица истинности:
0
0
0
1
1
1
0
1
0
0
0
1

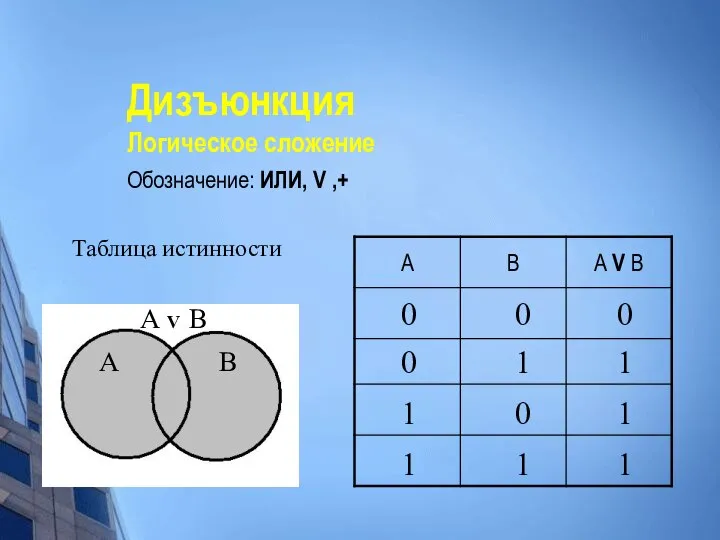
Дизъюнкция
Логическое сложение
Обозначение: ИЛИ, V ,+
Таблица истинности
0
0
0
1
1
1
0
1
0
1
1
1

Инверсия
Логическое отрицание
Обозначение: НЕ, ┐ , –
Таблица истинности
0
1
1
0

Постройте отрицания приведенных ниже высказываний:
Вася купил мороженое.
(Вася не купил мороженое.)
Существует шестое чувство.
(Не существует шестого чувства.)
На улице идет дождь.
Сегодня рабочий день.
Денис сегодня был готов к уроку.
В школу привезли новые компьютеры.

Являются ли отрицанием следующие высказывания:
Он – мой друг. Он – мой враг.
Большой дом. Небольшой дом.
Большой дом. Маленький дом.
X < 2. X > 2.

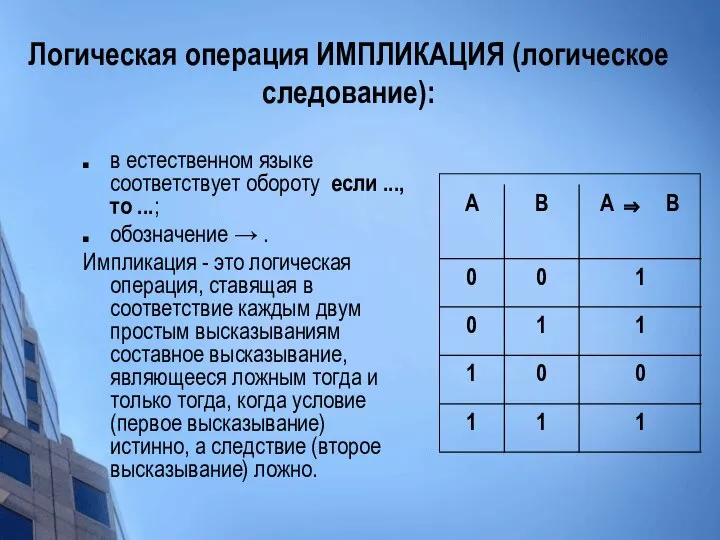
Логическая операция ИМПЛИКАЦИЯ (логическое следование):
в естественном языке соответствует обороту если ..., то ...;
обозначение → .
Импликация - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.

Логическая операция ЭКВИВАЛЕНЦИЯ (равнозначность):
в естественном языке соответствует оборотам речи тогда и только тогда; в том и только в том случае;
обозначения ⇔ , ~ .
Эквиваленция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.

Порядок выполнения логических операций:
Операции в скобках
Инверсия – НЕ
Конъюнкция – И
Дизъюнкция – ИЛИ
Импликация – ЕСЛИ…, ТО
Эквивалентность – ТОГДА И ТОЛЬКО ТОГДА, КОГДА

Логические операции
Каждое составное высказывание можно выразить в виде формулы (логического выражения), в которую войдут логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции.
ИСТИНА – 1
ЛОЖЬ - 0
Таблица истинности определяет значение сложного высказывания при всех возможных значениях простых высказываний

Инверсия - логическое отрицание
От лат. inversio - переворачиваю
Логическое отрицание делает истинное высказывание ложным и, наоборот, ложное – истинным.
Таблица истинности функции логического отрицания
Пример: Даны высказывания
А – «Число 10 – четное» = ИСТИНА
В – «Число 10 – отрицательное» = ЛОЖЬ
С – «Луна – спутник Земли» = ИСТИНА
Не А – «Неверно, что число 10 – четное» = ЛОЖЬ
Не В – «Неверно, что число 10 – отрицательное» = ИСТИНА
Не С – «Неверно, что Луна – спутник Земли» = ЛОЖЬ
В переводе на естественный язык
«Не А»
«Неверно, что А»
ИСТИНА – 1
ЛОЖЬ - 0

Конъюнкция - логическое умножение
От лат. conjunctio - связываю
Результат логического умножения является истинным тогда и только тогда, когда истинны все входящие в него простые высказывания.
Таблица истинности функции логического умножения
В переводе на естественный язык
«и А, и В» «как А, так и В»
«А вместе с В» «А несмотря на В»
«А, в то время как В»
И , , and, &, *, ·
Пример: Даны высказывания
А – «Число 10 – четное» = ИСТИНА
В – «Число 10 – отрицательное» = ЛОЖЬ
С – «Число 10 кратно 2» = ИСТИНА
А и В – «Число 10 – четное и отрицательное» - ЛОЖЬ
А и С – «Число 10 как четное, так и кратно 2» - ИСТИНА

Дизъюнкция - логическое сложение
От лат. disjunctio – различаю
Результат логического сложения является истинным тогда, когда истинно хотя бы одно из входящих в него простых высказываний.
В переводе на естественный язык
«А или В»
Таблица истинности функции логического сложения
Пример: Даны высказывания
А – «Число 10 – четное» = ИСТИНА
В – «Число 10 – отрицательное» = ЛОЖЬ
С – «Число 10 - простое» = ЛОЖЬ
А или В – «Число 10 – четное или отрицательное» - ИСТИНА
А или С – «Число 10 четное или простое» - ИСТИНА
В или С – «Число 10 отрицательное или простое» - ЛОЖЬ
ИЛИ, , or, +

Импликация - логическое следование
Результат логического следования является ложным тогда и только тогда, когда из истины следует ложь.
От лат. implicatio – тесно связывать
Таблица истинности функции логического следования
А – условие, В - следствие
В переводе на естественный язык
«если А, то В» «В, если А»
«Когда А, тогда В»
«А достаточно для В»
«А только тогда, когда В»
Пример: Даны высказывания
А – «Число 10 – четное» = ИСТИНА
В – «Число 10 – отрицательное» = ЛОЖЬ
С – «Число 10 - простое» = ЛОЖЬ
А В – «Если число 10 – четное,
то оно - отрицательное» - ЛОЖЬ
А С – «Число 10 простое, если четное» - ЛОЖЬ
«Если число делится на 10, то оно делится на 5» ИСТИНА

Эквивалентность - логическое равенство
Результат логического равенства является истинным тогда и только тогда, когда оба высказывания одновременно либо истинны, либо ложны.
От лат. aeguivalens – равноценное
Таблица истинности функции логического равенства
В переводе на естественный язык
«А эквивалентно В» «А тогда и только тогда, когда В»
=,
Пример: Даны высказывания
А – «Число 10 – четное» = ИСТИНА
В – «Число 10 – отрицательное» = ЛОЖЬ
С – «Число 10 - простое» = ЛОЖЬ
А В – «Число 10 – четное, тогда и только тогда, когда оно - отрицательное» - ЛОЖЬ
В С – «Число 10 такое же простое, как и отрицательное» ИСТИНА