Алгоритмы и анализ сложности. Эффективные алгоритмы сортировки

Задача сортировки элементов массива

Рекуррентное слияние (снизу вверх)

Рекуррентное слияние (снизу вверх)

Рекуррентный алгоритм слияния
void merge_sort(double *A, int n)
{
int s, b, c, e; double *D = new double[n];
for (s = 1; s < n; s *= 2) {
for (b = 0; b < n; b += s*2) {
c = min(b+s-1, n-1);
e = min(c+s, n-1);
merge_series(A, b, c, e, D);
}
for (b = 0; b < n; b++) A[b] = D[b];
}
delete [] D;
}

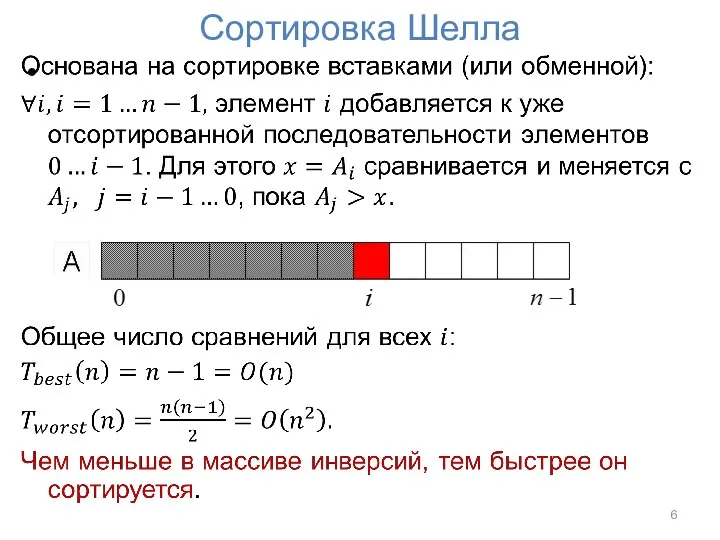
Сортировка Шелла

Сортировка Шелла: h-цепочки

Сортировка вставкам с шагом h

Сортировка Шелла: идея и требования

Сортировка Шелла: выбор шага h

Сортировка Шелла: алгоритм

Пирамидальная сортировка

Свойства пирамиды (бинарной кучи)

Идея сортировки

Построение пирамиды

Трудоемкость построения пирамиды

Трудоемкость построения пирамиды

Функция просеивания в пирамиде
Параметры и переменные функции sift:
i – начальный номер просеиваемого элемента,
m – номер конечного элемента в текущей пирамиде,
j – текущий номер просеиваемого элемента,
k – номер левого или большего сына j.
void sift(double *A, int i, int m)
{
int j = i, k = i*2+1; // левый сын
while (k <= m)
{
if (k
if (A[j] < A[k])
{ swap(A[j], A[k]); j = k; k = k*2+1; }
else break;
}
}

Алгоритм пирамидальной сортировки
void heap_sort(double *A, int n)
{
int i, m;
// построение пирамиды
for (i = n/2; i >= 0; i--)
sift(A, i, n-1);
// сортировка массива
for (m = n-1; m >= 1; m--)
{
swap(A[0], A[m]);
sift(A, 0, m-1);
}
}

Быстрая сортировка (Хоар)

Быстрая сортировка

Быстрая сортировка: трудоемкость в среднем

Трудоемкость в среднем: доказательство

Трудоемкость в среднем: доказательство

Трудоемкость в среднем: доказательство
Таким образом:

Разделение массива: 1-й способ

Разделение массива: 2-й способ

Быстрая сортировка с 2 рекурсивными вызовами
void quick_sort_2(double *A, int b, int e)
{ double x; int i, j;
x = A[(b+e)/2]; i = b; j = e;
while (i < j)
{
while (A[i] < x) i++;
while (A[j] > x) j--;
if (i <= j) {
{ swap(A[i], A[j]); i++; j--; }
}
if (b < j) quick_sort_2(A, b, j);
if (i < e) quick_sort_2(A, i, e);
}

Быстрая сортировка с 1 рекурсивным вызовом

Быстрая сортировка с 1 рекурсивным вызовом

Быстрая сортировка с 1 рекурсивным вызовом
void quick_sort(double *A, int b, int e)
{ double x; int i, j, c = b, d = e;
while (c < d) {
x = A[(c+d)/2]; i = c; j = d;
while (i < j) {
while (A[i] < x) i++;
while (A[j] > x) j--;
if (i <= j)
{ swap(A[i], A[j]); i++; j--; }
}
if (j-c < d-i)
{ if (c < j) quick_sort(A,c,j); c = i; }
else { if (i
}
}

Свойства алгоритмов сортировки

Поиск k-го минимального элемента

Поиск k-го минимального элемента