Содержание
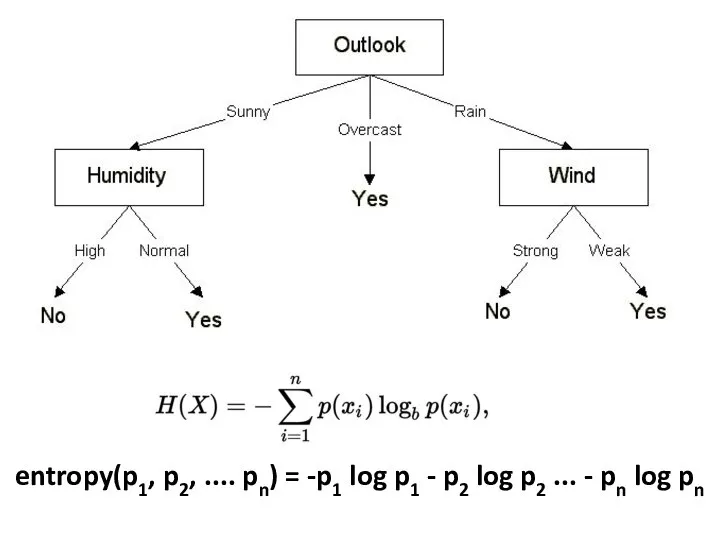
- 2. entropy(p1, p2, .... pn) = -p1 log p1 - p2 log p2 ... - pn log
- 3. This second law states that for any irreversible process, entropy always increases. Entropy is a measure
- 5. Entropy can be seen as a measure of the quality of energy: Low entropy sources of
- 6. - Claude Shannon transferred some of these ideas to the world of information processing. Information is
- 7. At the extreme of no information are random number. Of course, data may only look random.
- 8. A collection of random numbers has maximum entropy
- 9. Shannon defined the entropy Η (Greek capital letter eta) of a discrete variable X with possible
- 10. Presupunem evenimentul aruncării unui zar cu 6 fețe. Valorile variabilei X sunt {1,2,3,4,5,6} iar probabilitățile obținerii
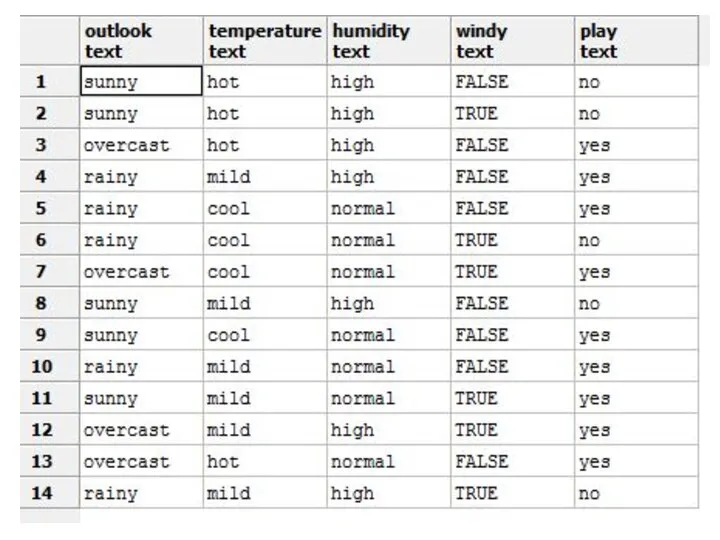
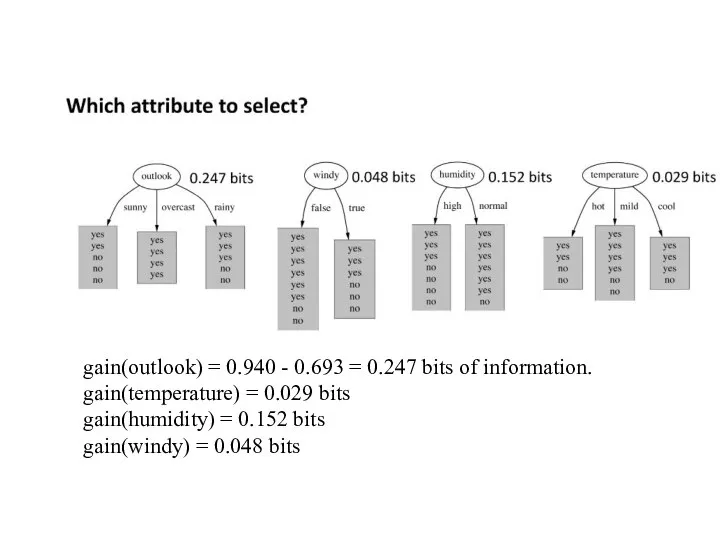
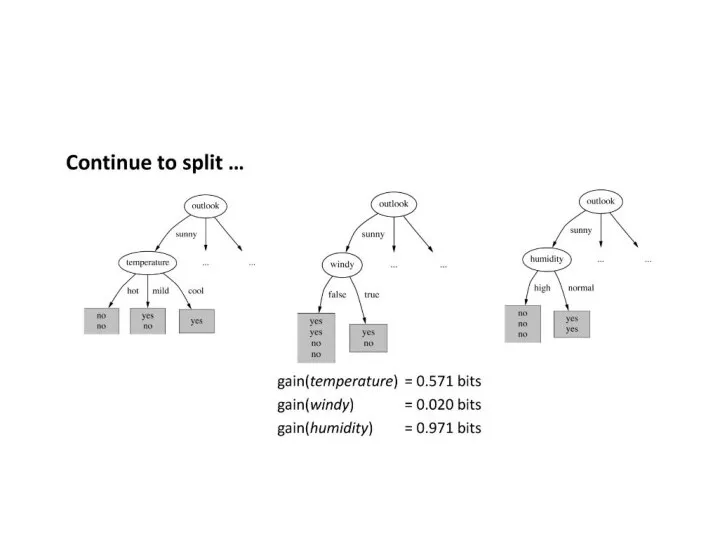
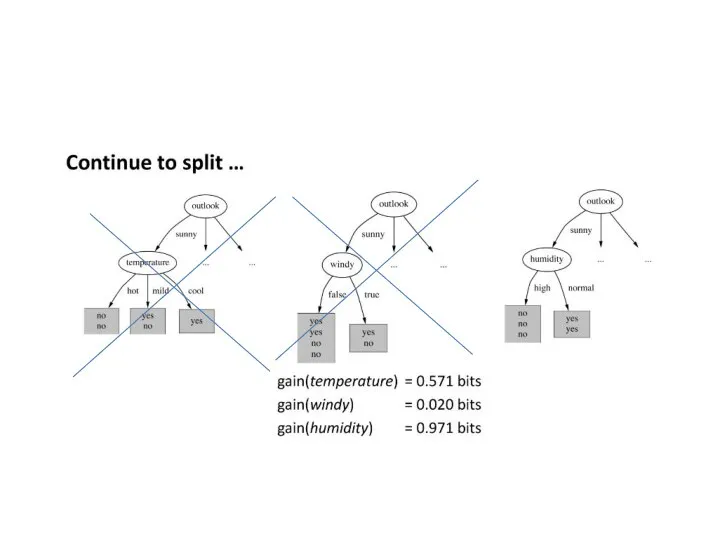
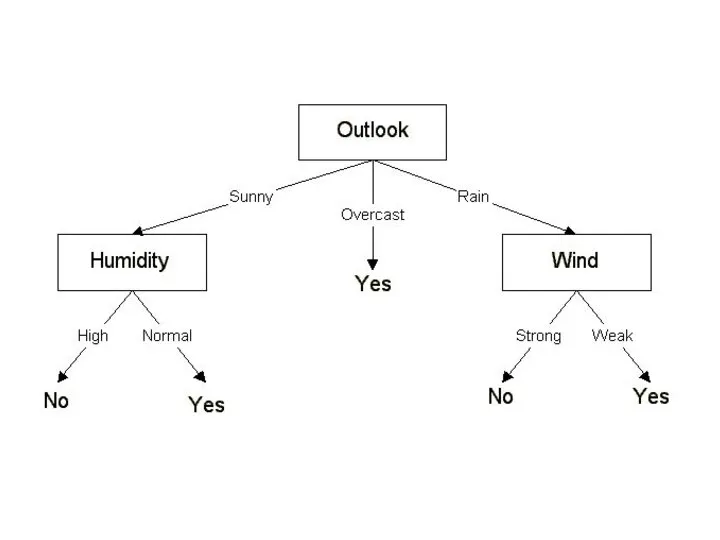
- 13. Entropyoutlook([2,3], [4,0],[3,2]) = (5/14) * 0.971 + (4/14) * 0.0 + (5/14) * 0.971 = 0.693bits
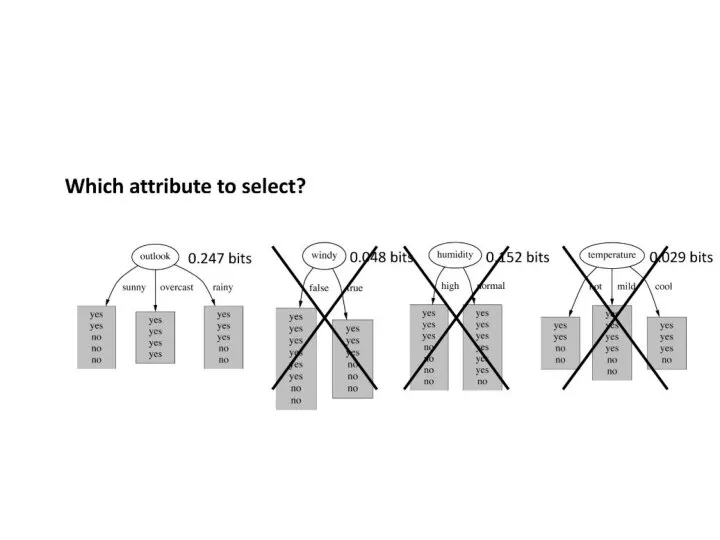
- 14. gain(outlook) = 0.940 - 0.693 = 0.247 bits of information. gain(temperature) = 0.029 bits gain(humidity) =
- 20. Скачать презентацию









![Entropyoutlook([2,3], [4,0],[3,2]) = (5/14) * 0.971 + (4/14) * 0.0 + (5/14)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1107637/slide-12.jpg)
 Информационно-библиотечный центр
Информационно-библиотечный центр Киберпреступники
Киберпреступники Администрирование 2020-2
Администрирование 2020-2 CorelDRAW
CorelDRAW Алгоритм это выполнения команд последовательность
Алгоритм это выполнения команд последовательность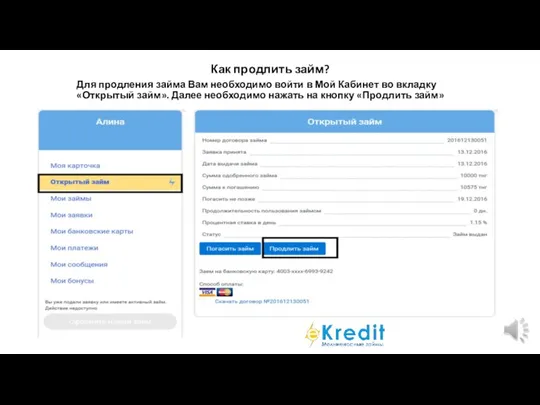 Как продлить займ
Как продлить займ Архитектура компьютера
Архитектура компьютера Вконтакте. Моя страница
Вконтакте. Моя страница Массивы. Класс Array
Массивы. Класс Array Интро. Аналитик в IT
Интро. Аналитик в IT Сайт Student City
Сайт Student City Разработка, создание и программирование работы термогигрометра на базе датчика DHT11 и Arduino
Разработка, создание и программирование работы термогигрометра на базе датчика DHT11 и Arduino История информатики. Носители информации
История информатики. Носители информации Производные типы данных: массивы
Производные типы данных: массивы Shox International Hospital. Международная больница Шокс
Shox International Hospital. Международная больница Шокс Создание сайта на тему ’’вредоносное ПО и вирусы’’
Создание сайта на тему ’’вредоносное ПО и вирусы’’ Константы
Константы Проект Фабрика согласия (пропаганда и цензура)
Проект Фабрика согласия (пропаганда и цензура) Язык SQL. Базы данных № 3-4
Язык SQL. Базы данных № 3-4 Работа с записями базы данных
Работа с записями базы данных Формализация Тьюринга
Формализация Тьюринга Карта социологических организаций и информационных ресурсов России
Карта социологических организаций и информационных ресурсов России Сортировка и фильтрация в EXCEL
Сортировка и фильтрация в EXCEL Информационные технологии в реализации взаимодействия власти и общества современной России
Информационные технологии в реализации взаимодействия власти и общества современной России Introduction to IT
Introduction to IT Интерактивная модульная дорожка
Интерактивная модульная дорожка Система документирования радиолокационной информации
Система документирования радиолокационной информации Обзор программных продуктов дистрибутива Линукс Юниор
Обзор программных продуктов дистрибутива Линукс Юниор