Машинное обучение: от базовых понятий до решения нестандартных задач. Временные ряды (Лекция 4)

Временные ряды и их свойства
Модель ARIMA
Метрики точности прогноза
Одномерное и многомерное прогнозирование
Прогнозирование как задача машинного обучения
Кросс-валидация на временных ряда
Нейронные сети в зачах предсказания временных рядов
Колонтитул
План

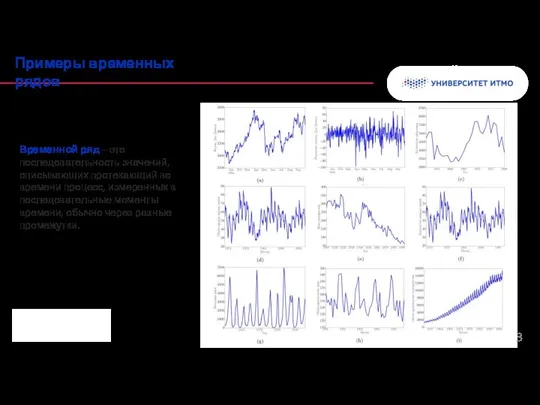
Временной ряд – это последовательность значений, описывающих протекающий во времени процесс, измеренных в последовательные моменты времени, обычно через равные промежутки.
Колонтитул
Примеры временных рядов

Свойства временных рядов:
Тренд
Сезонность
Цикл(ы)
Ошибки (шум)
Стационарность
Колонтитул
Анализ временных рядов
Задачи:
Поиск аномалий
Поиск локальных трендов
(локальные) максимумы и минимумы
Корреляция с внешними характеристиками (новости, внешние переменные, стоимость валюты и т. д.)
ПРОГНОЗИРОВАНИЕ

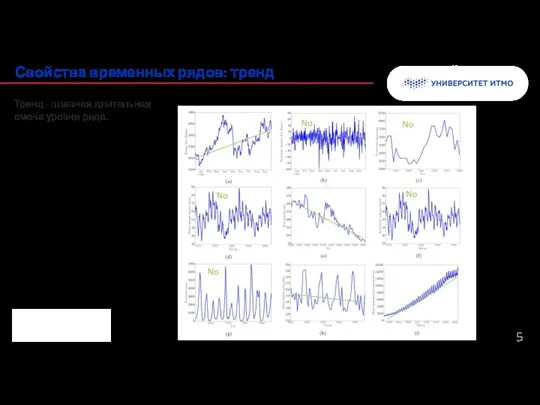
Колонтитул
Свойства временных рядов: тренд
Тренд - плавная длительная
смена уровня ряда.

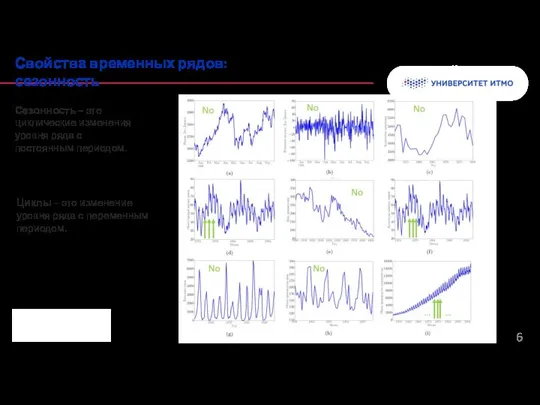
Колонтитул
Свойства временных рядов: сезонность
Сезонность – это циклические изменения уровня ряда с
постоянным периодом.
Циклы – это изменение уровня ряда с переменным периодом.

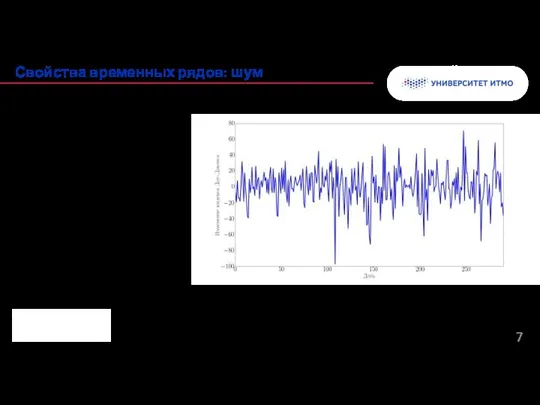
Колонтитул
Свойства временных рядов: шум
несистематическое поведение: нет тренда, нет сезонности, нет циклов…
случайная составляющая;
~ небольшие отклонения;
Шум – это непредсказуемый случайный компонент временных рядов.

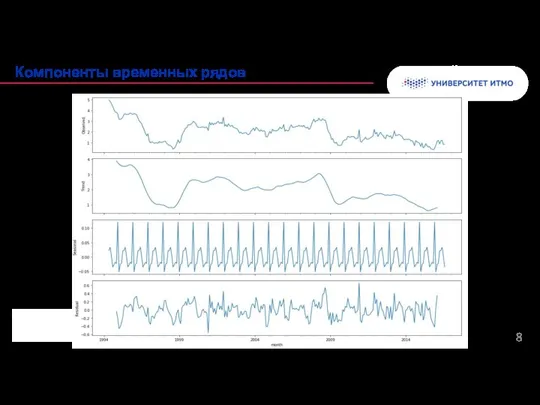
Колонтитул
Компоненты временных рядов

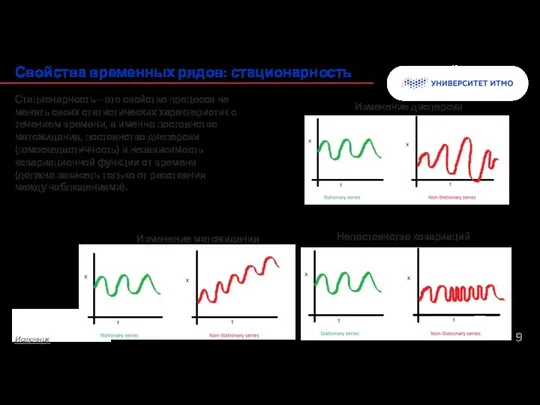
Колонтитул
Свойства временных рядов: стационарность
Стационарность – это свойство процесса не менять своих статистических характеристик с течением времени, а именно постоянство матожидания, постоянство дисперсии (гомоскедастичность) и независимость ковариационной функции от времени (должна зависеть только от расстояния между наблюдениями).
Источник
Изменение матожидания
Изменение дисперсии
Непостоянство ковариаций

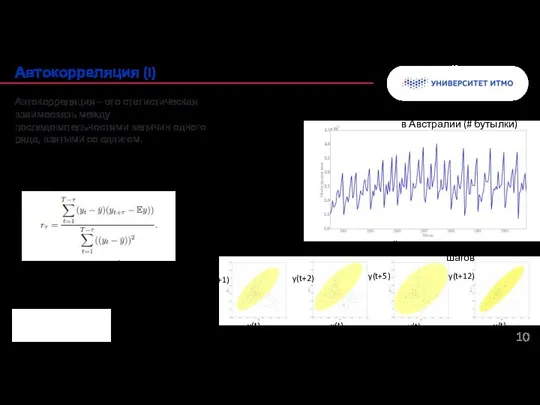
Колонтитул
Автокорреляция (I)
Зависимость значений от предыдущих шагов
y(t+1)
y(t+2)
y(t+5)
y(t+12)
y(t)
y(t)
y(t)
y(t)
Автокорреляция – это статистическая взаимосвязь между последовательностями величин одного ряда, взятыми со сдвигом.
Ежемесячный объем продаж вина
в Австралии (# бутылки)

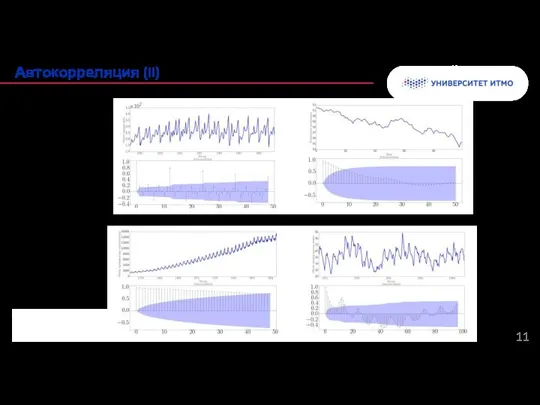
Примеры:
Колонтитул
Автокорреляция (II)

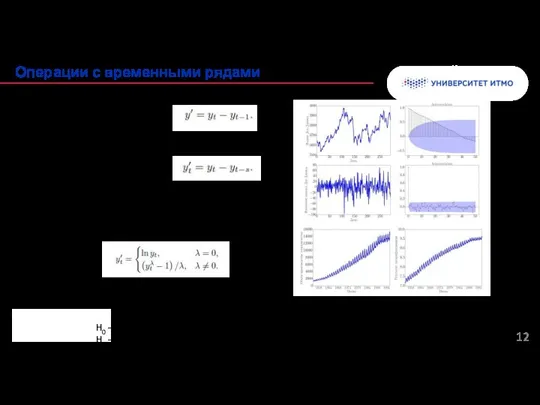
Дифференцирование
(derivative):
Сезонное дифференцирование
Seasonal derivative:
Нормализация дисперсии (преобразование Бокса-Кокса):
Тест на стационарность (Критерий Дики-Фуллера):
H0 – non-stationarity
H1 – stationarity
Колонтитул
Операции с временными рядами

autoregressive integrated moving average
Показывает хорошие результаты в прогнозировании авторегрессионных временных рядов с сильной сезонностью;
Необходима индивидуальная тонкая настройка для каждого нового примера.
Колонтитул
Модель ARIMA (I)
AR(p), авторегрессионная компонента:
MA(q), компонента скользящего среднего:
ARMA(p,q):
Компоненты:

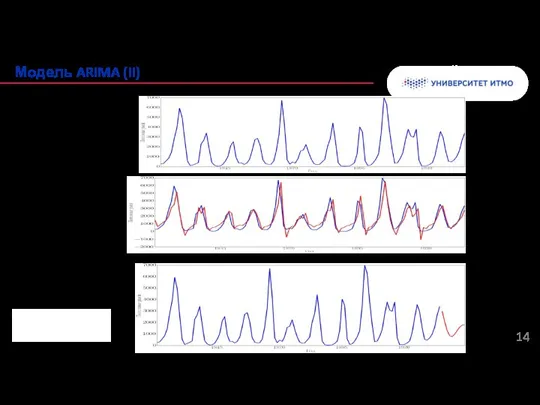
Колонтитул
Модель ARIMA (II)
ARMA(2,2)

Колонтитул
Модель ARIMA (III)
Wold’s theorem:
Каждый стационарный временной ряд может быть аппроксимирован моделью ARMA (p, q) с заданной точностью.
Временной ряд должен быть стационарен:
Преобразование Бокса-Кокса (log)
Дифференцирование (одношаговое или сезонное)
ARIMA(p,d,q) – модель ARMA для временных рядов, где d-порядок дифференцирования (взятия последовательной разности)
Сезонность
+ P components with period S
+ Q components with period S
SARMA(p,q)x(P,Q)

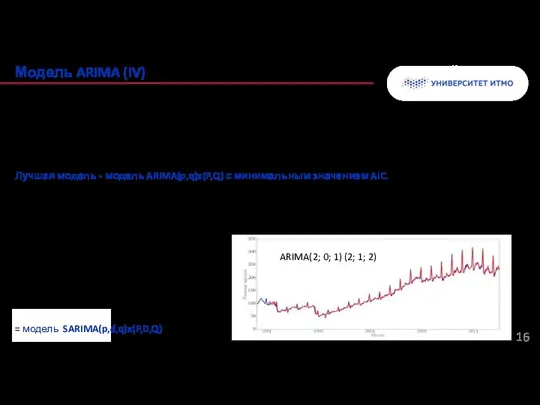
Необходимо найти значения (P,Q,p,q).
Минимизация информационного критерия Акаике (Akaike info criterion): AIC = 2 lnL + 2k
L - Функция правдоподобия
k = P + Q + p + q + 1 – число параметров модели
Лучшая модель - модель ARIMA(p,q)x(P,Q) с минимальным значением AIC.
Колонтитул
Модель ARIMA (IV)
ARIMA(2; 0; 1) (2; 1; 2)
SARMA(p,q)x(P,Q)
+ d – порядок дифференцирования
+ D – порядок сезонного дифференцирования
= модель SARIMA(p,d,q)x(P,D,Q)

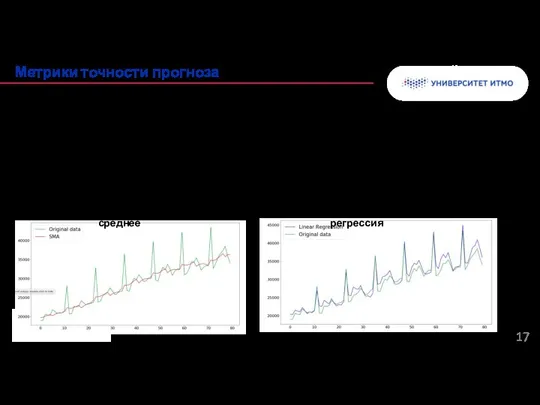
Пример. Сравним две модели:
линейная регрессия
скользящее среднее значение.
График ниже иллюстрирует результат прогнозирования моделей на тестовом наборе данных.
Колонтитул
Метрики точности прогноза
Скользящее среднее
Линейная регрессия

Метрики оценки точности прогноза:
R2
MSE (RMSE) – mean squared error – среднеквадратичная ошибка
MAE – mean absolute error – средняя абсолютная ошибка
MAPE – mean absolute percentage error – средняя абсолютная ошибка в %
SMAPE – symmetric mean absolute percentage error – симметричная средняя абсолютная ошибка в %
Колонтитул
Метрики точности прогноза

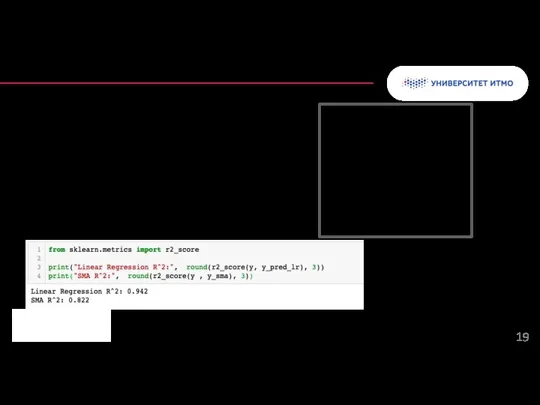
Метрики точности прогноза: R2

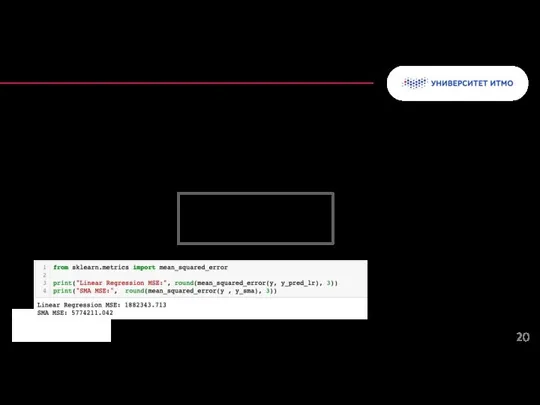
Среднеквадратичная ошибка (MSE) измеряет среднее значение квадратов ошибок, то есть среднеквадратичную разность между прогнозируемыми и фактическими значениями.
Всегда неотрицательна.
Значения ближе к нулю лучше.
Метрики точности прогноза: MSE

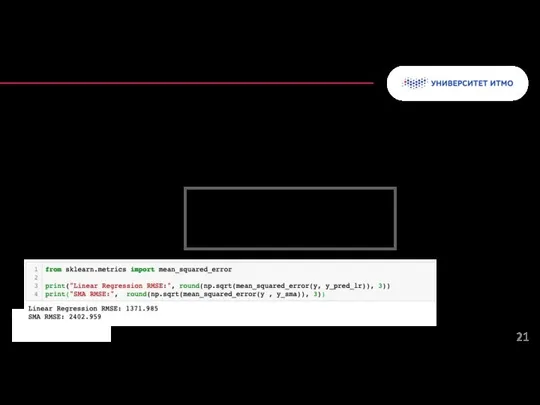
Среднеквадратичная ошибка - это корень из среднего квадрата разности между прогнозируемыми и фактическими значениями.
Всегда неотрицательна.
Значения ближе к нулю лучше.
Метрики точности прогноза: RMSE

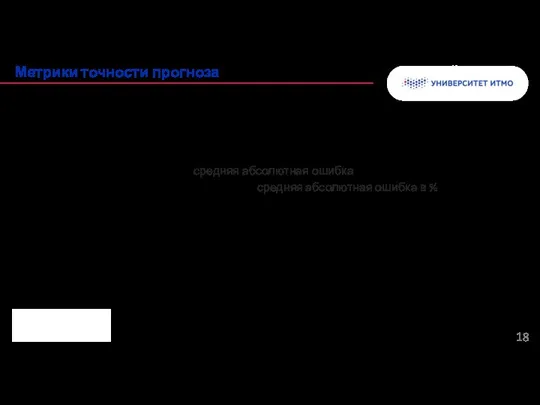
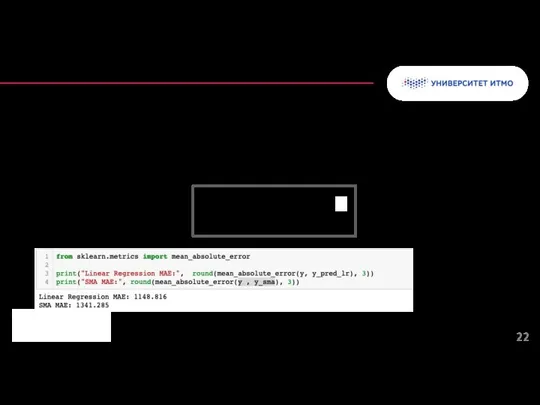
Средняя абсолютная ошибка - это среднее расстояние по вертикали между каждой прогнозируемой точкой и фактической линией.
Метрики точности прогноза: MAE

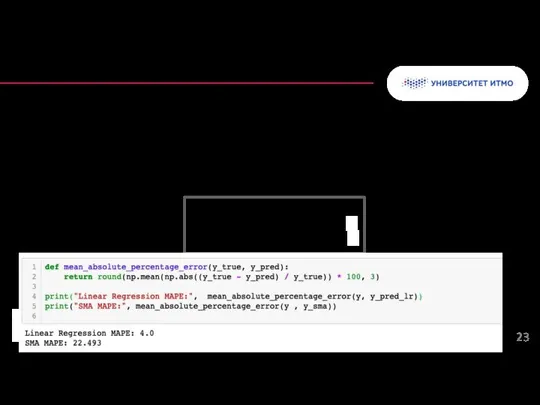
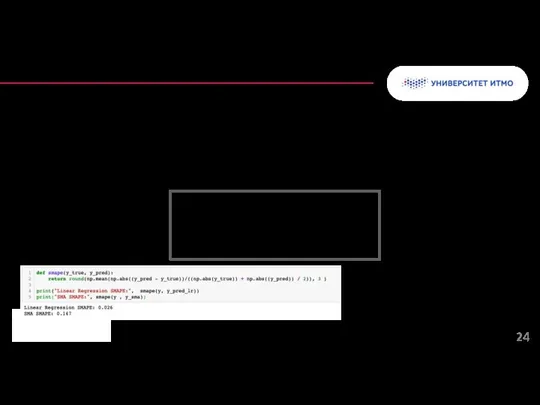
Средняя абсолютная процентная ошибка (MAPE) показывает среднюю долю ошибки относительно фактического значения. MAPE обычно выражает точность в процентах.
Нельзя использовать, если есть нулевые значения, потому что будет деление на ноль.
Для слишком низких прогнозов процентная ошибка не может превышать 100%, но для слишком высоких прогнозов нет верхнего предела процентной ошибки.
Метрики точности прогноза: MAPE

Симметричная средняя абсолютная ошибка в процентах - это показатель точности, основанный на процентах.
Абсолютная разница между фактическим значением и прогнозируемым значением делится на половину суммы абсолютных значений фактического значения и прогнозируемого значения. Значение этого вычисления суммируется для каждой подобранной точки t и снова делится на количество подобранных точек n.
Метрики точности прогноза: SMAPE

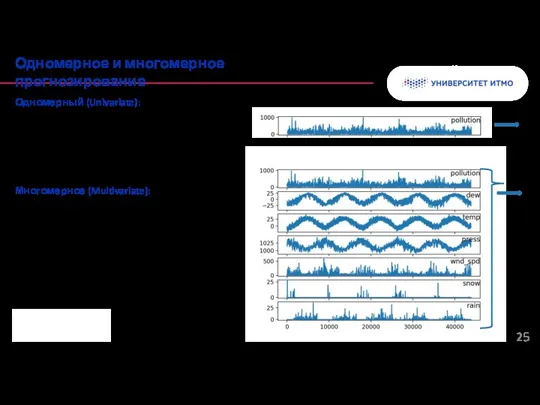
Одномерный (Univariate):
Один целевой временной ряд
Прогнозирование только на его основе
Многомерное (Multivariate):
Один целевой временной ряд
Несколько характеристик за один и тот же период времени, которые могут повлиять на результат (курс валюты, температура, уровень безработицы и др.)
Прогноз на основе полных данных
Колонтитул
Одномерное и многомерное прогнозирование

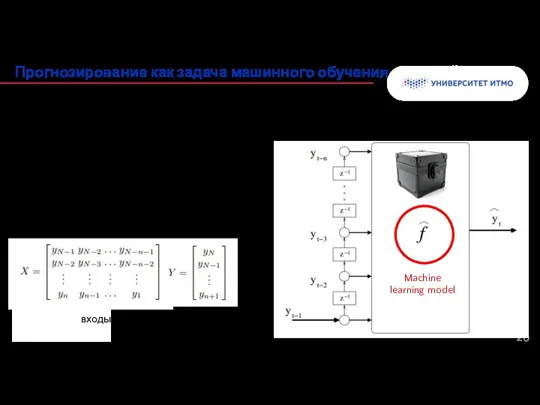
Прогнозирование на один шаг вперед. Задача обучения с учителем.
Необходимые данные:
обучающий набор (входы)
метки (выходам)
и тестовый набор
Временной ряд: S: [y0, y1, ….. yt-2, yt-1]
Предсказываем
Колонтитул
Прогнозирование как задача машинного обучения
входы
выходы
Machine learning model

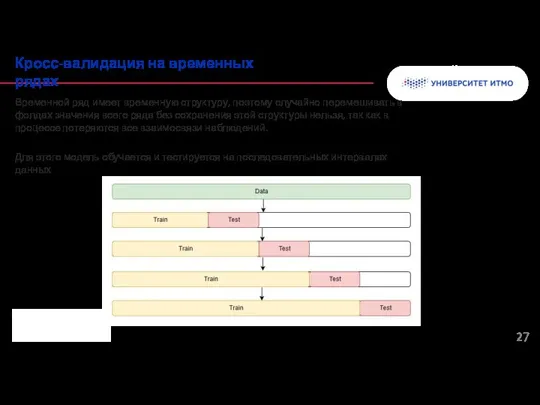
Временной ряд имеет временную структуру, поэтому случайно перемешивать в фолдах значения всего ряда без сохранения этой структуры нельзя, так как в процессе потеряются все взаимосвязи наблюдений.
Для этого модель обучается и тестируется на последовательных интервалах данных
Колонтитул
Кросс-валидация на временных рядах

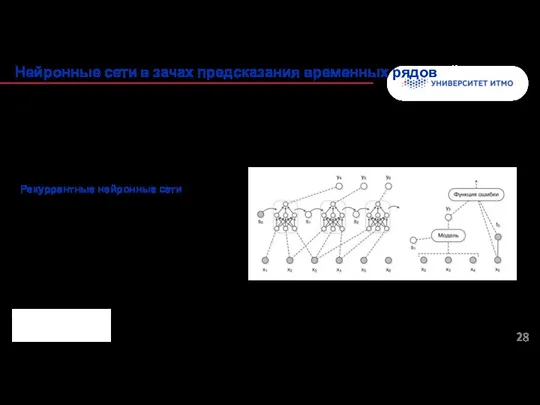
Модель должна «помнить» элементы последовательности с целью использовать их в дальнейшем;
Необходимо фиксировать зависимости с большим временным окном.
Колонтитул
Нейронные сети в зачах предсказания временных рядов
Рекуррентные нейронные сети - это вид нейронных сетей, где связи между элементами образуют направленную последовательность. Благодаря этому появляется возможность обрабатывать серии событий во времени или последовательные пространственные цепочки.

Афанасьев В.Н., Юзбашев М.М. Анализ временных рядов и прогнозирование — М.: Финансы и статистика, 2001. — 228 с.:
Портал https://machinelearningmastery.com/
Статья: https://habr.com/ru/company/ods/blog/327242/
Колонтитул
Список дополнительной литературы

Для оценки точности прогноза с нулевыми значениями в фактических данных нельзя использовать:
R2
MAPE
MSE
2) Что не относится к операциям, которые используются для преобразования временного ряда к стационарному:
Дифференцирование
Масштабирование
Преобразование Бокса-Кокса
Колонтитул
Вопросы для самоконтроля
Ответы на вопросы можно найти в файле «ответы.docx»