Арифметические операции в позиционных системах счисления. Представление информации в компьютере. 10 класс

Ключевые слова
позиционные системы счисления
арифметические операции в системе счисления с основанием q
таблица сложения
таблица умножения

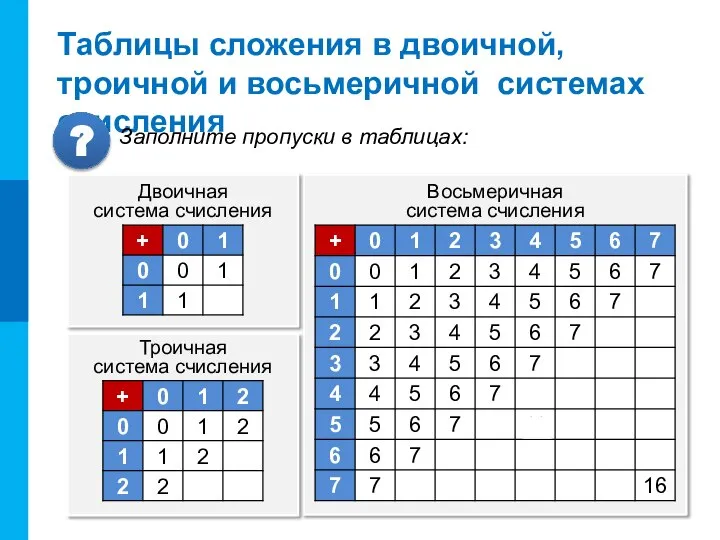
Таблицы сложения в двоичной, троичной и восьмеричной системах счисления
Двоичная
система счисления
Восьмеричная
система счисления
Троичная система счисления
Заполните пропуски в таблицах:
?

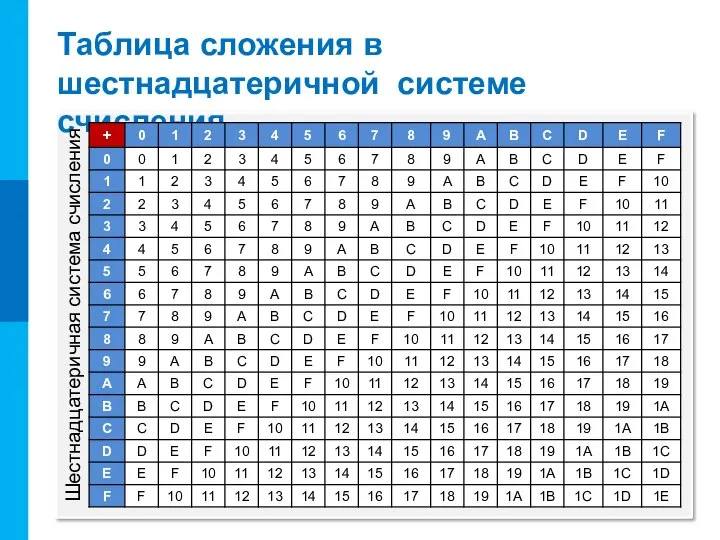
Таблица сложения в шестнадцатеричной системе счисления
Шестнадцатеричная система счисления

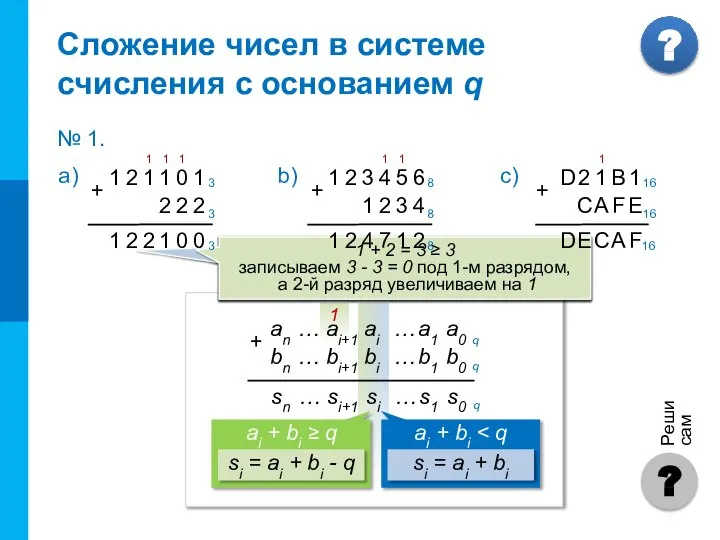
1
Чтобы в системе счисления с основанием q получить сумму S двух чисел A и B, надо просуммировать образующие их цифры по разрядам i справа налево:
Сложение чисел в системе счисления
с основанием q
если ai + bi < q, то si = ai + bi,
старший (i + 1)-й разряд не изменяется
если ai + bi ≥ q, то si = ai + bi – q,
старший (i + 1)-й разряд увеличивается на 1

1 + 2 = 3 ≥ 3
записываем 3 – 3 = 0 под 2-м разрядом,
а 3-й разряд увеличиваем на 1
1 + 1 + 2 = 4 ≥ 3
записываем 4 – 3 = 1 под 3-м разрядом,
а 4-й разряд увеличиваем на 1
1 + 1 = 2 < 3
записываем 2 под 4-м разрядом
1 + 2 = 3 ≥ 3
записываем 3 - 3 = 0 под 1-м разрядом,
а 2-й разряд увеличиваем на 1
1
2
4
7
1
2
1
1
8
b)
D
E
C
A
F
1
16
c)
Сложение чисел в системе
счисления с основанием q
3
а)
?
Реши сам
№ 1.
1
2
2
1
0
0
1
1
1

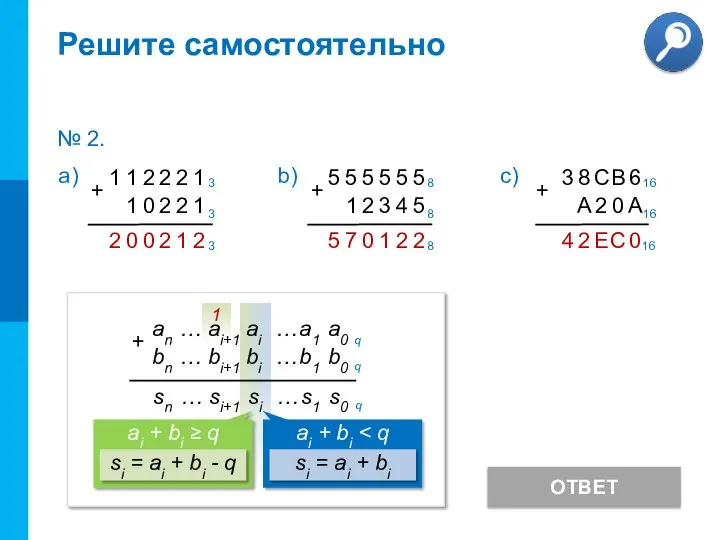
Решите самостоятельно
ОТВЕТ
№ 2.

●
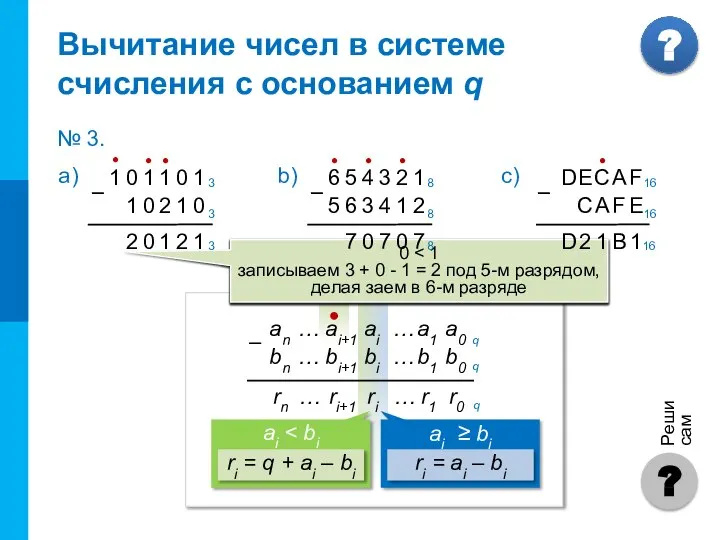
Чтобы в системе счисления с основанием q получить разность R двух чисел A и B, надо вычислить разности образующих их цифр по разрядам i справа налево:
Вычитание чисел в системе счисления
с основанием q
если ai ≥ bi, то ri = ai – bi,
старший (i + 1)-й разряд не изменяется
если a i < b i , то ri = q + ai – bi ,
старший (i + 1)-й разряд уменьшается на 1

0 = 0
записываем 0 под 4-м разрядом
0 < 2
записываем 3 + 0 - 2 = 1 под 3-м разрядом,
делая заем в 4-м разряде
0 < 1
записываем 3 + 0 – 1 = 2 под 2-м разрядом,
делая заем в 3-м разряде
1 ≥ 0
записываем 1 - 0 = 1 под 1-м разрядом
0 < 1
записываем 3 + 0 - 1 = 2 под 5-м разрядом,
делая заем в 6-м разряде
Вычитание чисел в системе
счисления с основанием q
?
Реши сам
2
0
1
2
1
●
●
3
а)
7
0
7
0
7
●
8
b)
D
2
1
B
1
●
16
c)
●
●
●
№ 3.

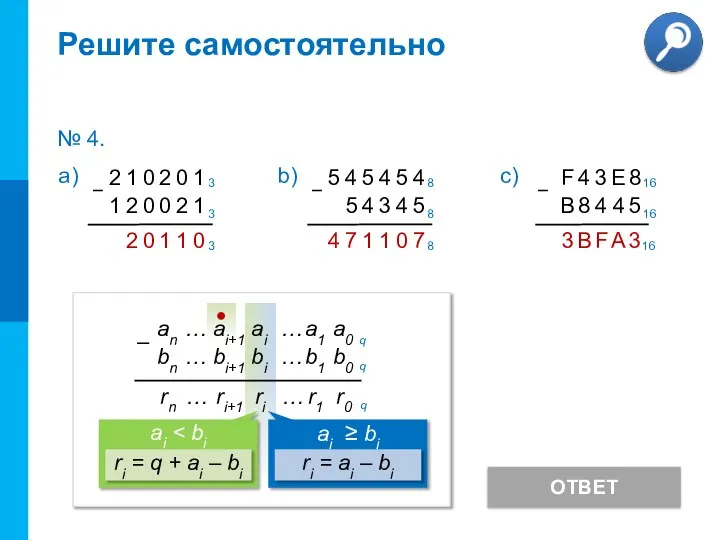
Решите самостоятельно
ОТВЕТ
№ 4.

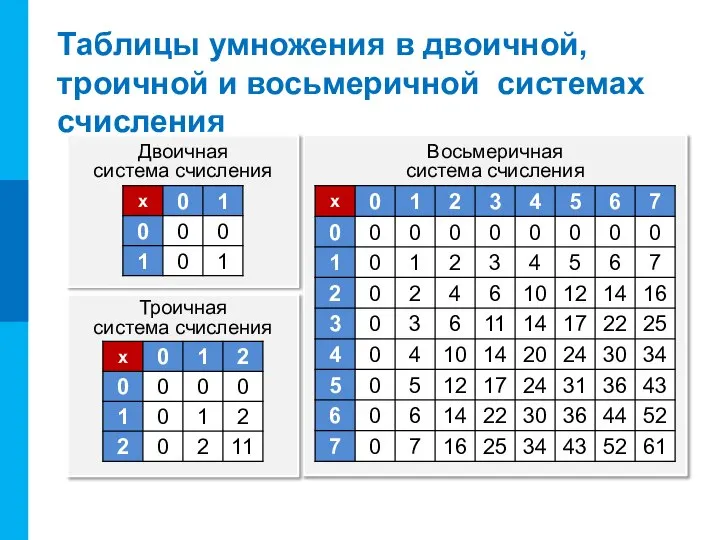
Таблицы умножения в двоичной, троичной и восьмеричной системах счисления
Двоичная
система счисления
Восьмеричная
система счисления
Троичная система счисления

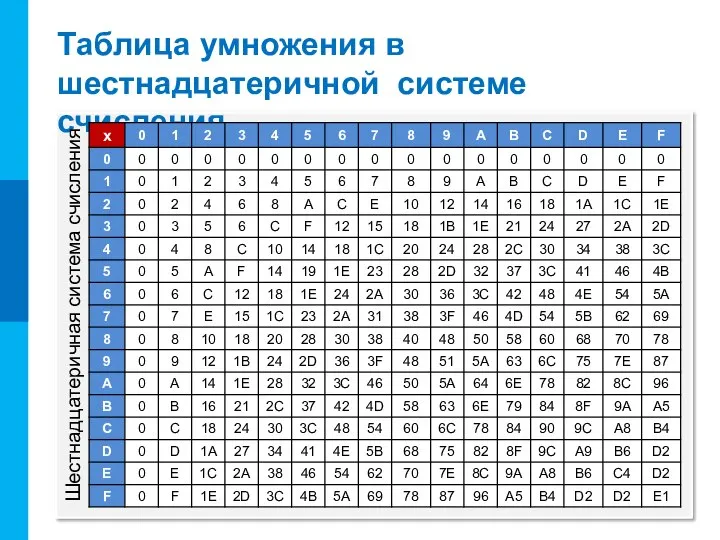
Таблица умножения в шестнадцатеричной системе счисления
Шестнадцатеричная система счисления

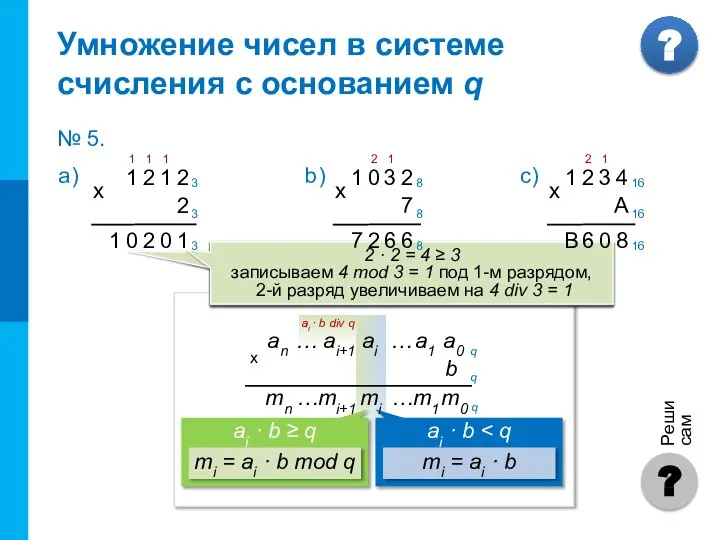
ai · b div q
Чтобы в системе счисления q получить произведение M многозначного числа A и однозначного числа b, надо вычислить произведения b и цифр числа A по разрядам i :
Умножение многозначного числа на однозначное в системе счисления q
если ai · b < q, то mi = ai · b,
старший (i + 1)-й разряд не изменяется
если ai · b ≥ q, то mi = ai · b mod q,
старший (i + 1)-й разряд увеличивается на ai · b div q

1 · 2 + 1 = 3 ≥ 3
записываем 3 mod 3 = 0 под 2-м разрядом,
3-й разряд увеличиваем на 3 div 3 = 1
2 · 2 + 1 = 3 ≥ 3
записываем 5 mod 3 = 2 под 3-м разрядом,
4-й разряд увеличиваем на 5 div 3 = 1
2 · 1 + 1 = 3 ≥ 3
записываем 3 mod 3 = 0 под 4-м разрядом
и в 5-й разряд записываем 3 div 3 = 1
2 · 2 = 4 ≥ 3
записываем 4 mod 3 = 1 под 1-м разрядом,
2-й разряд увеличиваем на 4 div 3 = 1
Умножение чисел в системе
счисления с основанием q
3
а)
7
2
6
6
2
1
8
b)
?
Реши сам
№ 5.
1
0
2
0
1
1
1
1
В
6
0
8
2
1
16
с)

Решите самостоятельно
ОТВЕТ
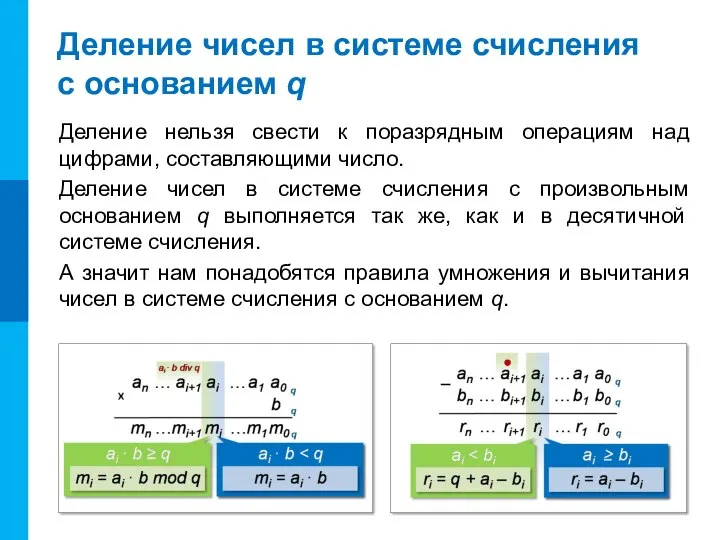
№ 6.

Деление нельзя свести к поразрядным операциям над цифрами, составляющими число.
Деление чисел в системе счисления с произвольным основанием q выполняется так же, как и в десятичной системе счисления.
А значит нам понадобятся правила умножения и вычитания чисел в системе счисления с основанием q.
Деление чисел в системе счисления
с основанием q

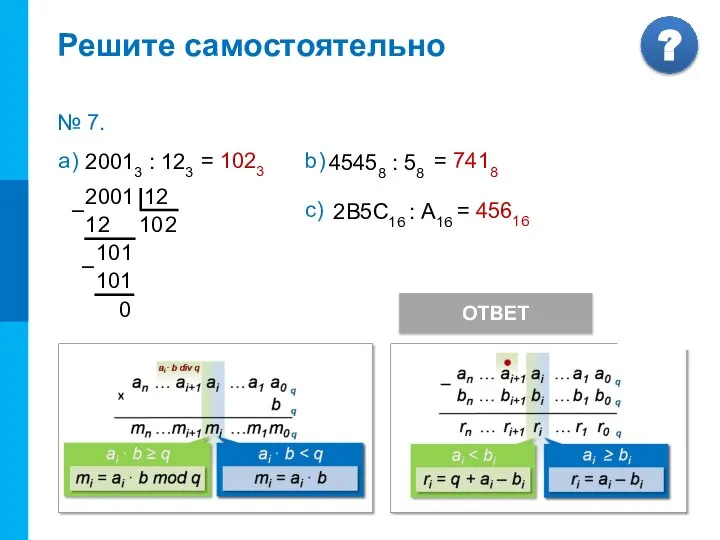
Деление чисел в системе
счисления с основанием q
а)
?
Реши сам
№ 7.
Решите самостоятельно
20013 : 123
1
12
= 1023
101
–
0
2
0
–
1
10
ОТВЕТ

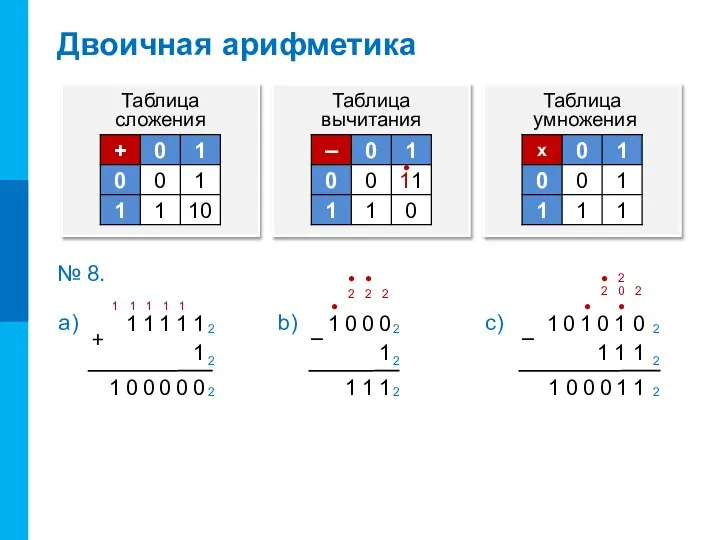
Двоичная арифметика
Таблица
сложения
Таблица
вычитания
Таблица умножения
●
0
0
0
0
0
1
1
1
2
а)
1
1
1
●
2
b)
1
●
●
№ 8.
1
1
2
2
2
0
0
0
1
1
●
2
c)
1
●
2
2
0
●
2

Исходное выражение 24000 + 42016 + 22018 – 8600 + 6
примет вид 24000 + 24032 + 22018 – 21800 + 22 + 21
Вопросы и задания
Задание 1. Найдём количество единиц в двоичной записи числа, являющегося результатом десятичного выражения
24000 + 42016 + 22018 – 8600 + 6.
Решение:
Представим все операнды исходного выражения в виде степеней двойки:
24000 + 42016 + 22018 – 8600 + 6
6 = 4 + 2 = 22 + 21
8600 = (23)600 = 21800
42016 = (22)2016 = 24032
Перепишем выражение в порядке убывания степеней:
24032 + 24000 + 22018 – 21800 + 22 + 21

Вопросы и задания
Для работы с десятичными числами вида 2n полезно иметь в виду следующие закономерности в их двоичной записи:
21 = 10 = 1 + 1; 22 = 100 = 11 + 1; 23 = 1000 = 111 + 1; …
24032 + 24000 + 22018 – 21800 + 22 + 21
Эти соотношения позволят подсчитать количество «1» в выраже-нии без вычислений. Двоичные представления чисел 24032 и 24000 внесут в двоичное представление суммы по одной «1». Разность 22018 – 21800 в двоичной записи представляет собой цепочку из 218 единиц и следующих за ними 1800 нулей. Слагаемые 22 и 21 дают ещё 2 единицы. Итого: 1 + 1 + 218 + 1 + 1 = 222.
Решение:

Вопросы и задания
Задание 2. Найдём количество цифр в восьмеричной записи числа, являющегося результатом десятичного выражения:
2299 + 2298 + 2297 + 2296.
Двоичное представление исходного числа имеет вид:
Решение:
Ответ: 100 цифр
Всего в этой записи 300 двоичных символов. При переводе двоичного числа в восьмеричную систему счисления каждая триада исходного числа заменяется восьмеричной цифрой.
Следовательно, восьмеричное представление исходного числа состоит из 100 цифр.

Самое главное
Арифметические операции в позиционных системах счисления с основанием q выполняются по правилам, аналогичным правилам, действующим в десятичной системе счисления.
Если необходимо вычислить значение арифметического выражения, операнды которого представлены в различных системах счисления, можно:
все операнды представить в привычной нам десятичной системе счисления;
вычислить результат выражения в десятичной системе счисления;
перевести результат в требуемую систему счисления.

Самое главное
Для работы с десятичными числами вида 2n полезно иметь в
виду следующие закономерности в их двоичной записи:
Для натуральных n и m таких, что n > m, получаем:

Вопросы и задания
1. Выполните арифметические операции над двоичными числами. Для того чтобы убедиться в правильности полученных результатов, найдите десятичные эквиваленты операндов и результата.
а) 1011110102 + 1001112
б) 10111,012 + 1,112
в) 101011012 - 111012
г) 110112 · 11012
д) 10110112 : 1112
ОТВЕТ

Вопросы и задания
2. Какое число следует за каждым из данных. Ответ для каждого числа дайте в указанной системе счисления.
а) 101112
б) 3445
в) 76778
г) EFF16
Какое число предшествует каждому из данных. Ответ для каждого числа дайте в указанной системе счисления.
ОТВЕТ
ОТВЕТ

Вопросы и задания
3. Сумму восьмеричных чисел
17 + 1 700 + 170 000 + 17 000 000 + 1 700 000 000
перевели в 16-теричную систему счисления. Найдите в
16-ной записи числа, равного этой сумме, 5-ю цифру слева.
Найдем сумму данных чисел.
В полученной сумме
10 восьмеричных цифр или
10·3 - 2 = 28 двоичных цифры или
28 : 4 = 7 тетрад
Нас интересует 5-я слева (она же
3-я справа) тетрада: 00112=316
Ответ: цифра 3
Решение:
111
001
111
001
111
00112=316
1