Содержание
- 2. Лекция 9. Числа в компьютере Машинные коды чисел Прямой код [x]пр [x]пр = x, при x
- 3. Лекция 9. Числа в компьютере Машинные коды чисел Обратный код [x]обр [x]обр. = x, при x
- 4. Лекция 9. Числа в компьютере Машинные коды чисел Дополнительный код [x]доп. [x]доп. = x, при x
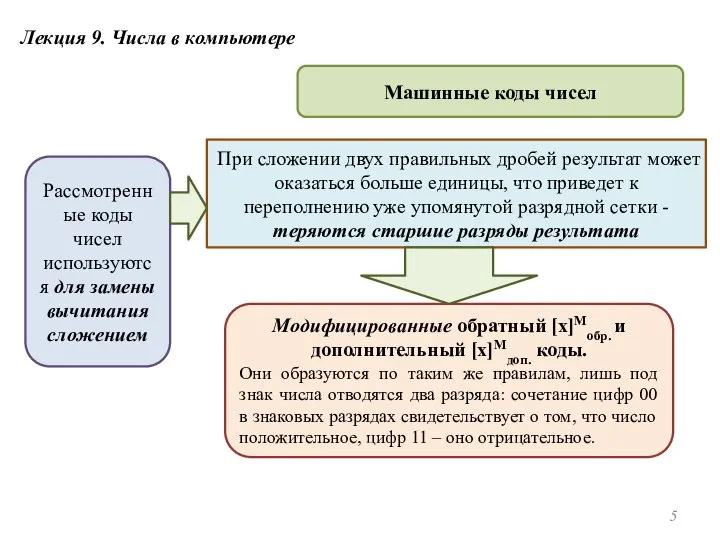
- 5. Лекция 9. Числа в компьютере Машинные коды чисел Рассмотренные коды чисел используются для замены вычитания сложением
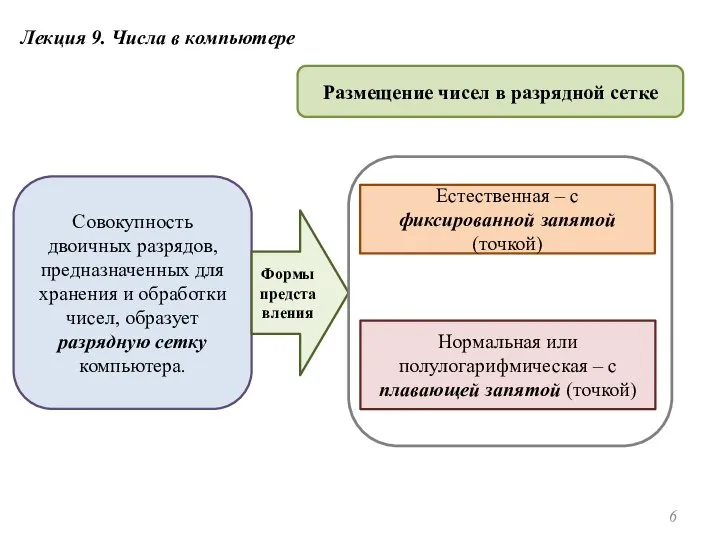
- 6. Лекция 9. Числа в компьютере Размещение чисел в разрядной сетке Совокупность двоичных разрядов, предназначенных для хранения
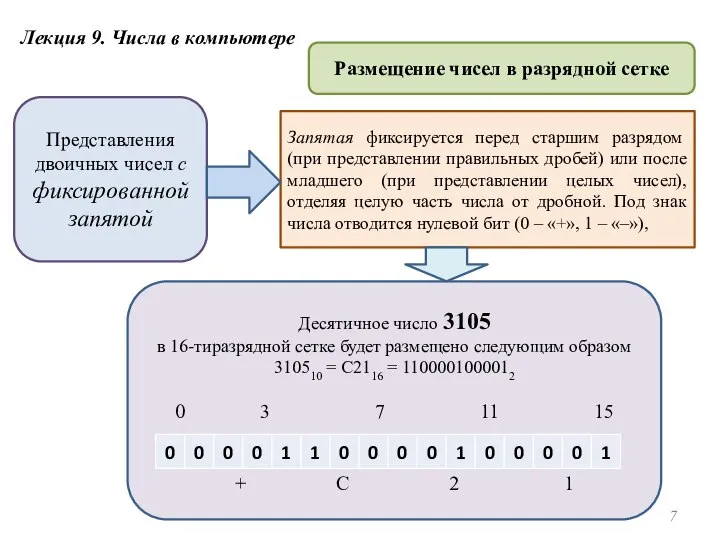
- 7. Лекция 9. Числа в компьютере Размещение чисел в разрядной сетке Представления двоичных чисел с фиксированной запятой
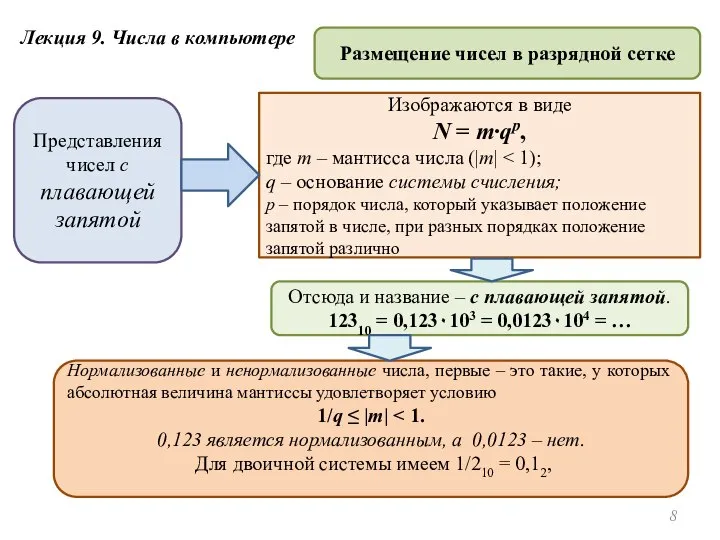
- 8. Лекция 9. Числа в компьютере Размещение чисел в разрядной сетке Представления чисел с плавающей запятой Изображаются
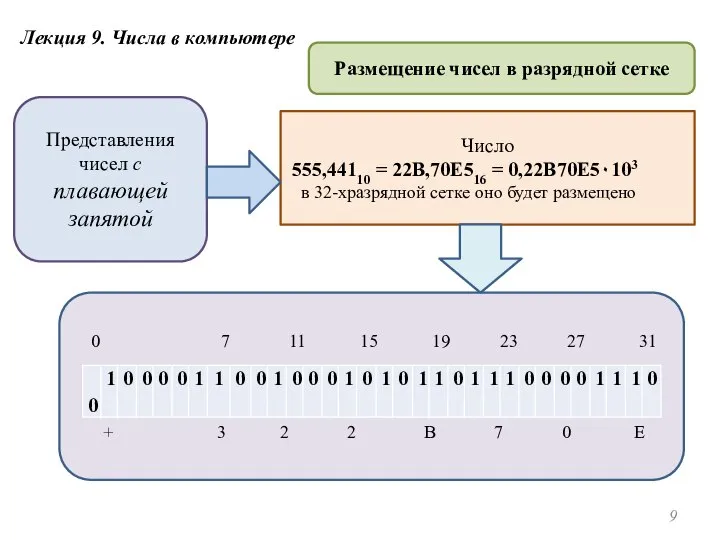
- 9. Лекция 9. Числа в компьютере Размещение чисел в разрядной сетке Представления чисел с плавающей запятой Число
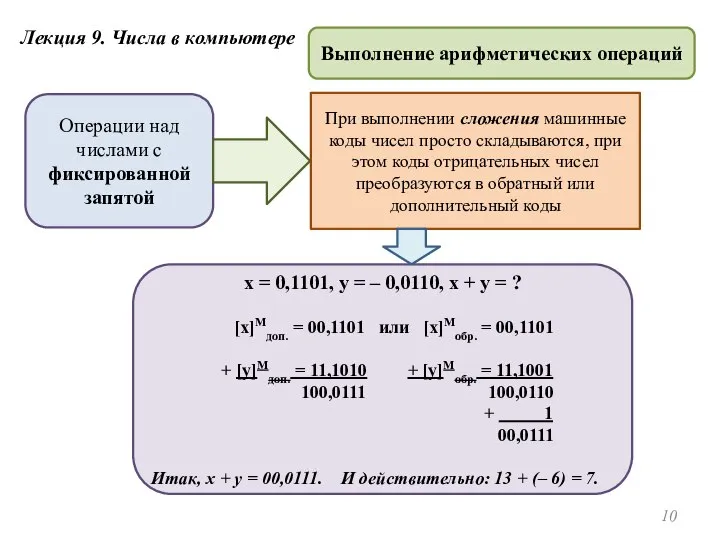
- 10. Лекция 9. Числа в компьютере Выполнение арифметических операций Операции над числами с фиксированной запятой При выполнении
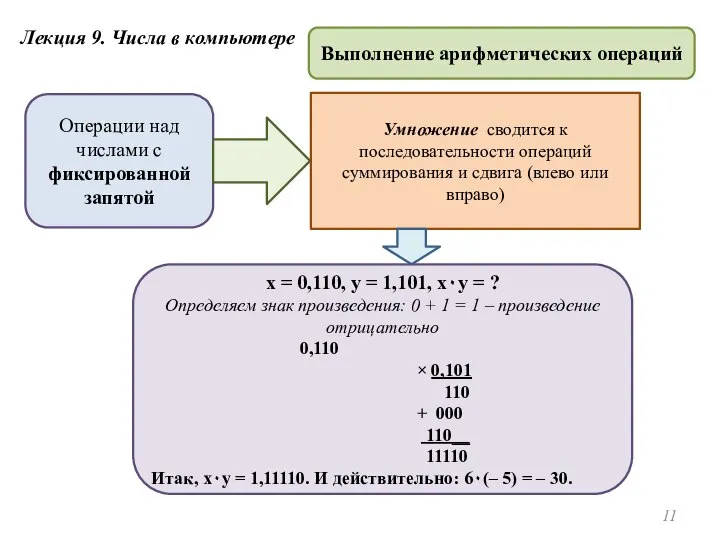
- 11. Лекция 9. Числа в компьютере Выполнение арифметических операций Операции над числами с фиксированной запятой Умножение сводится
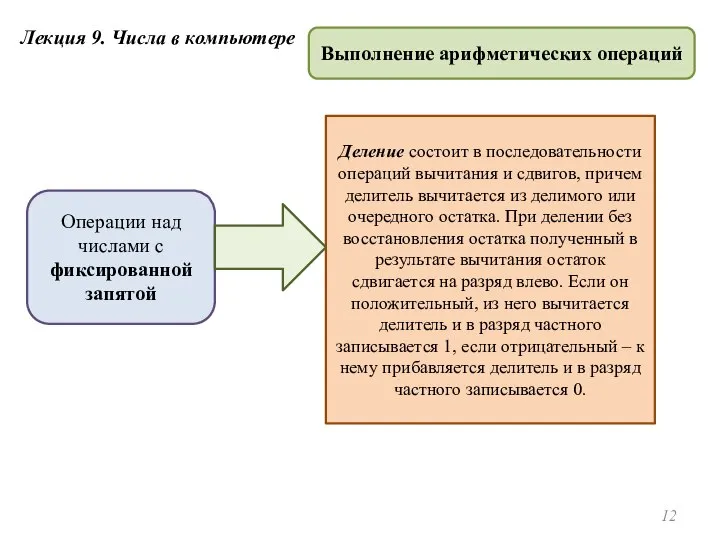
- 12. Лекция 9. Числа в компьютере Выполнение арифметических операций Операции над числами с фиксированной запятой Деление состоит
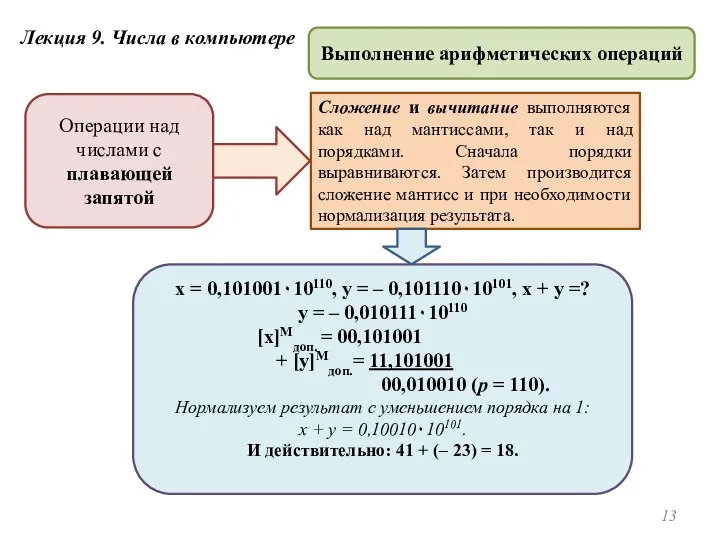
- 13. Лекция 9. Числа в компьютере Выполнение арифметических операций Операции над числами с плавающей запятой Сложение и
- 15. Скачать презентацию
![Лекция 9. Числа в компьютере Машинные коды чисел Прямой код [x]пр [x]пр](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1027286/slide-1.jpg)
![Лекция 9. Числа в компьютере Машинные коды чисел Обратный код [x]обр [x]обр.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1027286/slide-2.jpg)
![Лекция 9. Числа в компьютере Машинные коды чисел Дополнительный код [x]доп. [x]доп.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1027286/slide-3.jpg)
 Технология XPath, XQuery
Технология XPath, XQuery Методология , структура и преимущество ERP – систем, смысл новой идеологии CSRP, расширенное управление
Методология , структура и преимущество ERP – систем, смысл новой идеологии CSRP, расширенное управление Основы видеомонтажа
Основы видеомонтажа Аналіз трактування медіаосвіти науковцями
Аналіз трактування медіаосвіти науковцями Типы данных в VBA
Типы данных в VBA Разработка цифрового устройства
Разработка цифрового устройства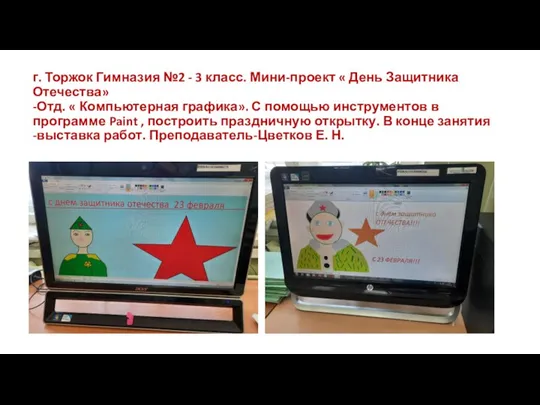 С помощью инструментов в программе Paint, построить праздничную открытку
С помощью инструментов в программе Paint, построить праздничную открытку Регистрация в Антиплагиат
Регистрация в Антиплагиат Система поиска информации о вертолетах
Система поиска информации о вертолетах Однотонная заливка светлым цветом
Однотонная заливка светлым цветом Языки и системы программирования
Языки и системы программирования XQsHfj8q6ya0LkEdgtAKXA
XQsHfj8q6ya0LkEdgtAKXA Разработка модели современной системы оплаты проезда в Санкт-Петербурге
Разработка модели современной системы оплаты проезда в Санкт-Петербурге Организация подпрограмм. Программирование на ЯВУ. Лекция 5
Организация подпрограмм. Программирование на ЯВУ. Лекция 5 Misrosoft Excel. Основы работы с программой. Часть 2
Misrosoft Excel. Основы работы с программой. Часть 2 Устройства компьютера
Устройства компьютера Основы программирования на Блюпринтах. Лекция 2
Основы программирования на Блюпринтах. Лекция 2 Устройство компьютера
Устройство компьютера Образовательный проект iiiiinstadeutsch
Образовательный проект iiiiinstadeutsch МПСвЭПиТК. Характеристики ПЛК
МПСвЭПиТК. Характеристики ПЛК Методы шифровки секретных сообщений. Смена-головоломка
Методы шифровки секретных сообщений. Смена-головоломка Электронные таблицы. Обработка числовой информации в электронных таблицах
Электронные таблицы. Обработка числовой информации в электронных таблицах Заполнение контента на pharmacosmetica
Заполнение контента на pharmacosmetica Язык структурированных запросов. Лекция №7
Язык структурированных запросов. Лекция №7 Библиотека, хранилище сокровищ цивилизации
Библиотека, хранилище сокровищ цивилизации Структуры данных. Запись
Структуры данных. Запись Методологии проектирования программного обеспечения
Методологии проектирования программного обеспечения Что такое SwapXI
Что такое SwapXI