нули в начале (слева) тоже записываются:
1. ААААА
2. ААААБ
3. ААААВ
4. АААБА
…
51. ?
200. ?
Вопросы и задания
Задание 3 (решение).
= 000003 = 010
= 000013 = 110
= 000023 = 210
= 000103 = 310
…
Чтобы понять, какое слово соответствует этому числу, надо перевести его в троич-ную систему счисления и при необходимости дополнить слева «0» до пяти разрядов.
На 51-м месте в списке стоит число 51-1 = 50, а на 200-м – число 200-1=199.
→ АБВБВ
5010 = 012123
= *****3 = 5010
= *****3 = 19910
Аналогично надо перевести в троичную систему счисления число 199.
→ ВББАБ
19910 = 211013
Ответ: АБВБВ и ВББАБ

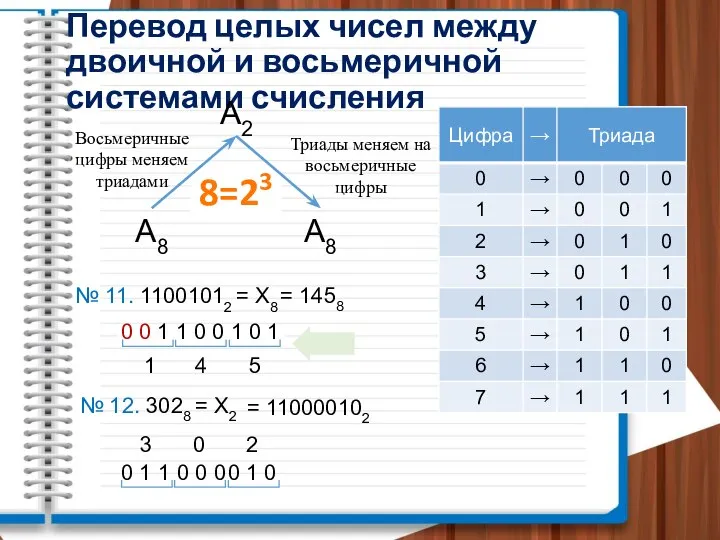
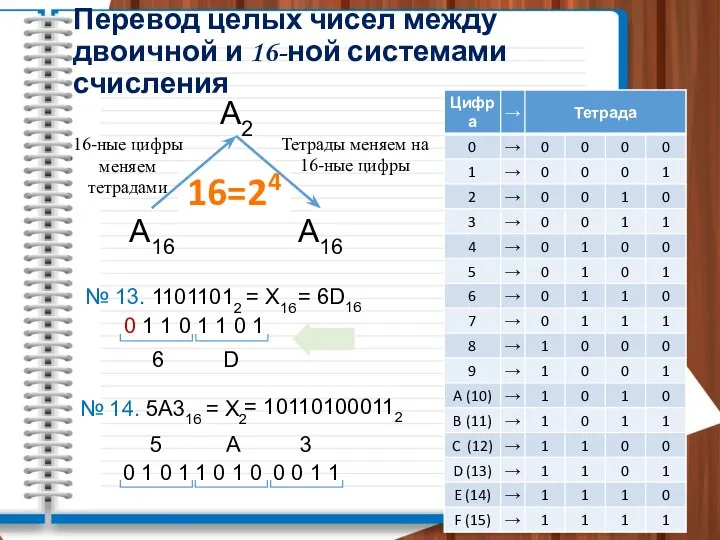

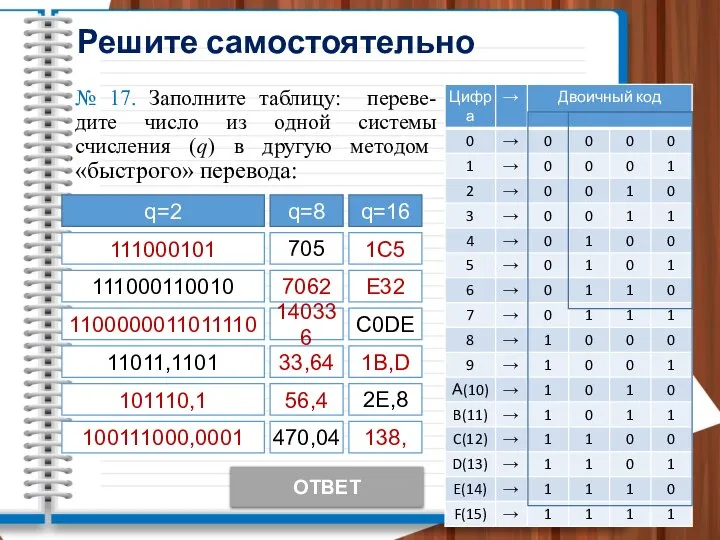


 Возможности электронных таблиц
Возможности электронных таблиц Живое общение для вашего бизнеса Наш сайт www.7-time.ru
Живое общение для вашего бизнеса Наш сайт www.7-time.ru Асимметричное шифрование
Асимметричное шифрование Лекция 3
Лекция 3 Разработка игры “Sokoban”
Разработка игры “Sokoban” 1_urok
1_urok Работа в ЛКА ЕФИН
Работа в ЛКА ЕФИН DeLion Steel. Проект
DeLion Steel. Проект Моделирование этапов обеспечения безопасности обмена информацией пользователей локальной сети
Моделирование этапов обеспечения безопасности обмена информацией пользователей локальной сети ВКР: Защита персональных данных в кадровой службе
ВКР: Защита персональных данных в кадровой службе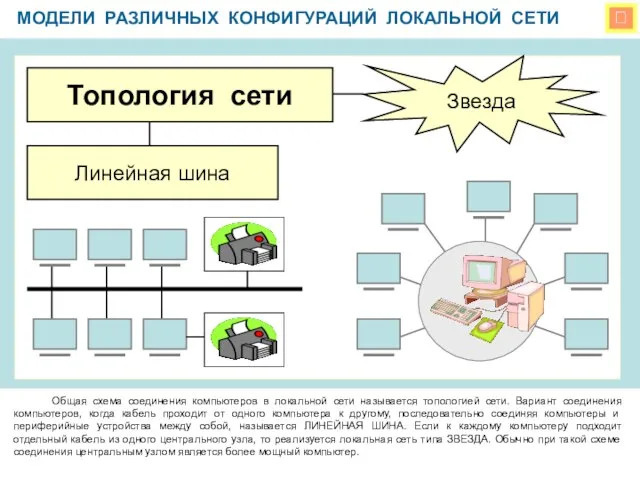 Модели различных конфигураций локальной сети
Модели различных конфигураций локальной сети Как свернуть информацию и запомнить текстМастер-класс
Как свернуть информацию и запомнить текстМастер-класс Беспроводной интернет: особенности его функционирования
Беспроводной интернет: особенности его функционирования логика
логика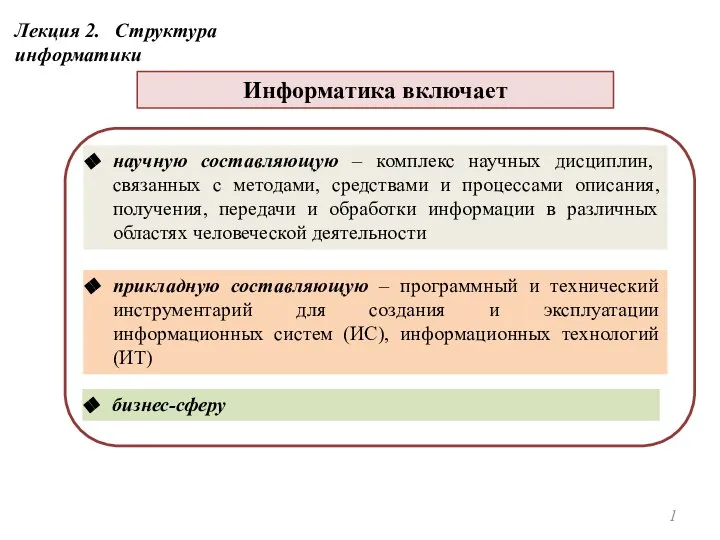 Структура информатики
Структура информатики Разработка приложений на языке высокого уровня
Разработка приложений на языке высокого уровня Создание веб-сайтов. Алгоритмика
Создание веб-сайтов. Алгоритмика Развитие саундтреков в играх
Развитие саундтреков в играх Разветвляющиеся вычислительные процессы (Практическая работа №2)
Разветвляющиеся вычислительные процессы (Практическая работа №2) Человек в цифровой среде (лекция 1)
Человек в цифровой среде (лекция 1) Непозиционные системы счисления
Непозиционные системы счисления Методы массивов. Метод массива splice
Методы массивов. Метод массива splice Знакомство с интерфейсом
Знакомство с интерфейсом Linux – веб-сервер
Linux – веб-сервер Летние уроки в Skysmart
Летние уроки в Skysmart 1 С
1 С Mit App Inventor. Экран, надпись, кнопка, блоки. Урок 1
Mit App Inventor. Экран, надпись, кнопка, блоки. Урок 1 How to Download and Install Epson Printers
How to Download and Install Epson Printers