Содержание
- 2. Acknowledgment Michael Theobald and Steven Nowick, for providing slides for this lecture.
- 3. An Implicit Method for Hazard-Free Two-Level Logic Minimization Michael Theobald and Steven M. Nowick Columbia University,
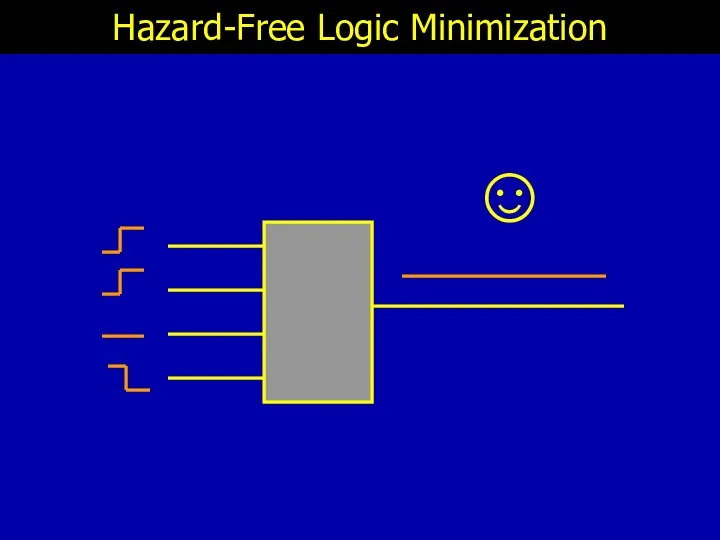
- 4. ☹ Hazard-Free Logic Minimization Given: Boolean function and multi-input change
- 5. ☺ Hazard-Free Logic Minimization
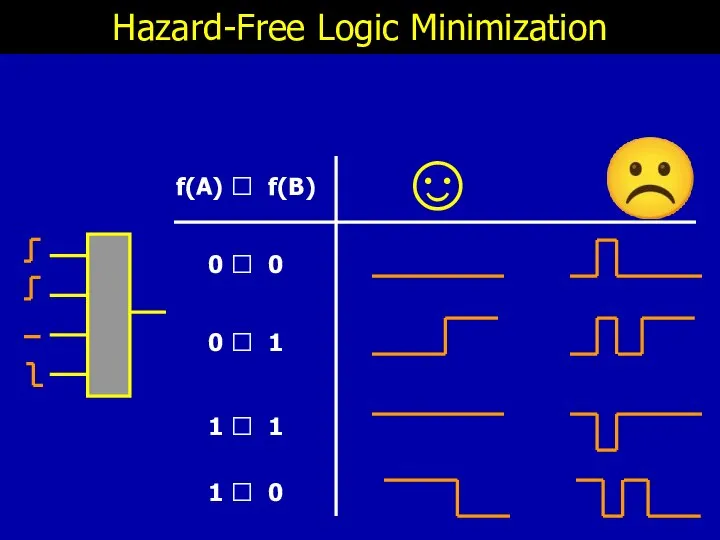
- 6. ☺ Hazard-Free Logic Minimization ☹ f(A) ? f(B) 0 ? 0 0 ? 1 1 ?
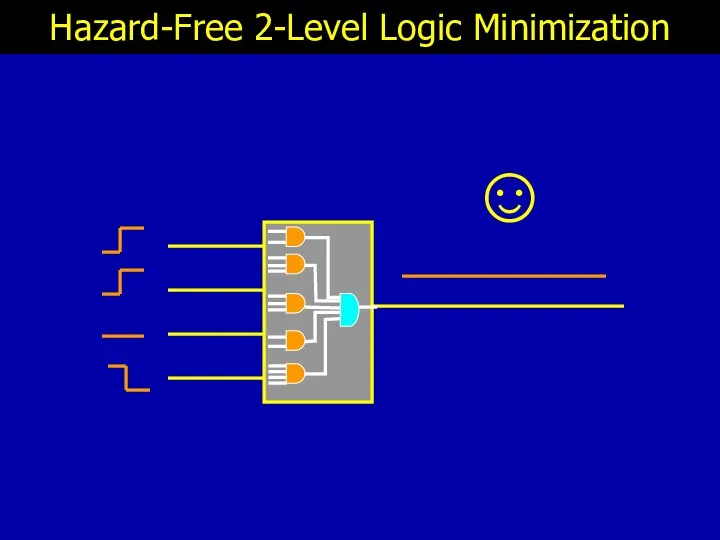
- 7. ☺ Hazard-Free 2-Level Logic Minimization
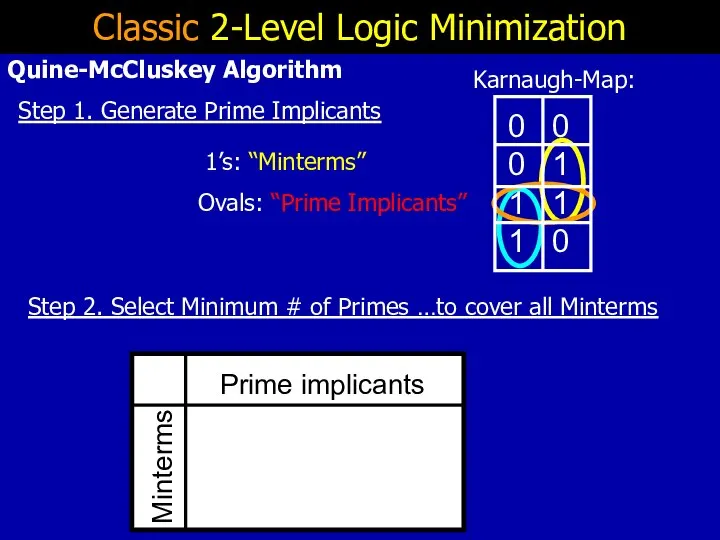
- 8. Classic 2-Level Logic Minimization Step 1. Generate Prime Implicants Step 2. Select Minimum # of Primes
- 9. 2-level Logic Minimization: Classic vs. Hazard-Free Classic (Quine-McCluskey): Hazard-Free: Given: Boolean function & set of “multi-input”
- 10. Hazard-Free Logic Minimization Non-monotonic function hazard no implementation hazard-free Monotonic function-hazard-free ☺ ☹ Restriction to monotonic
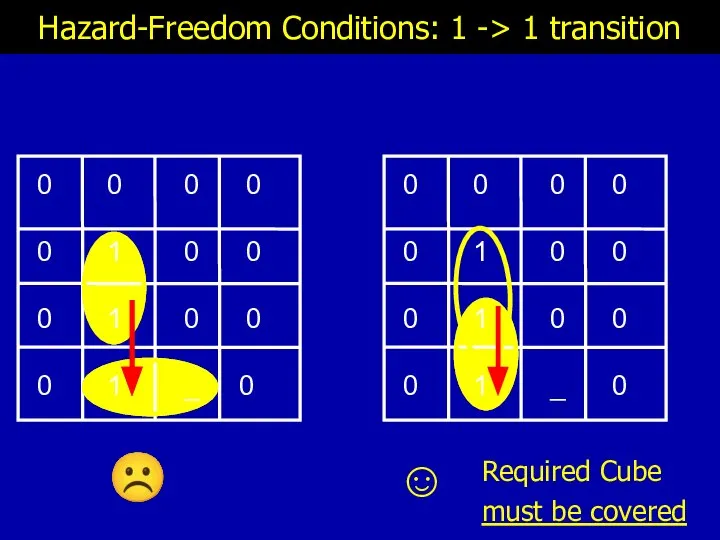
- 11. Hazard-Freedom Conditions: 1 -> 1 transition ☺ ☹ Required Cube must be covered
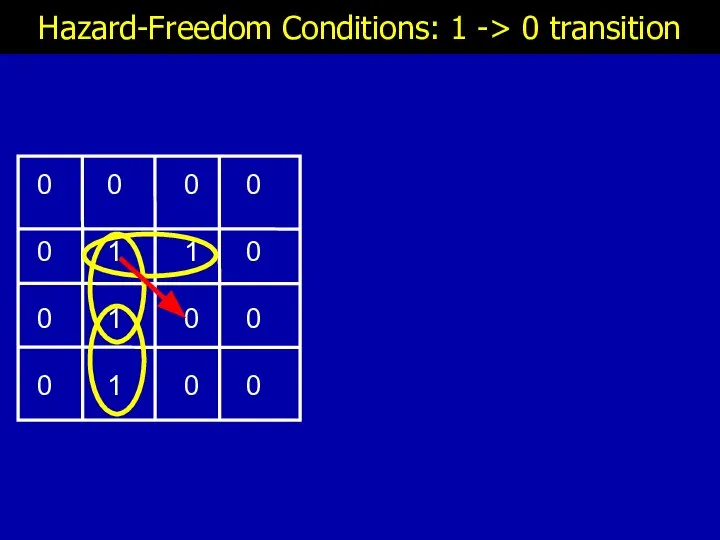
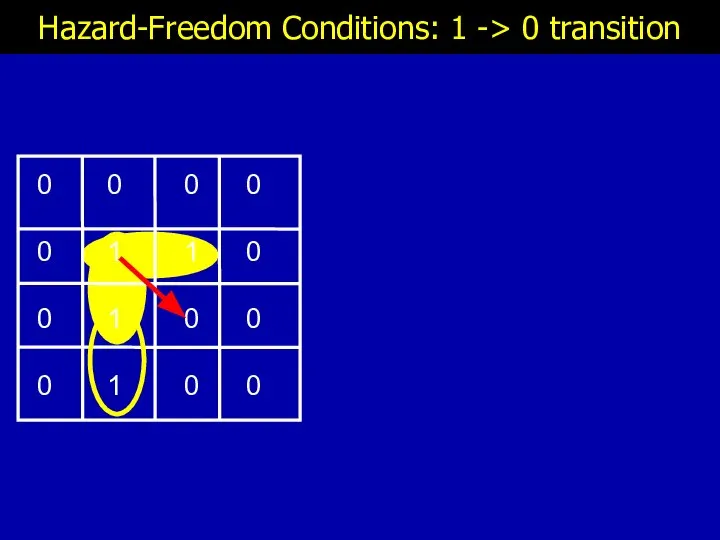
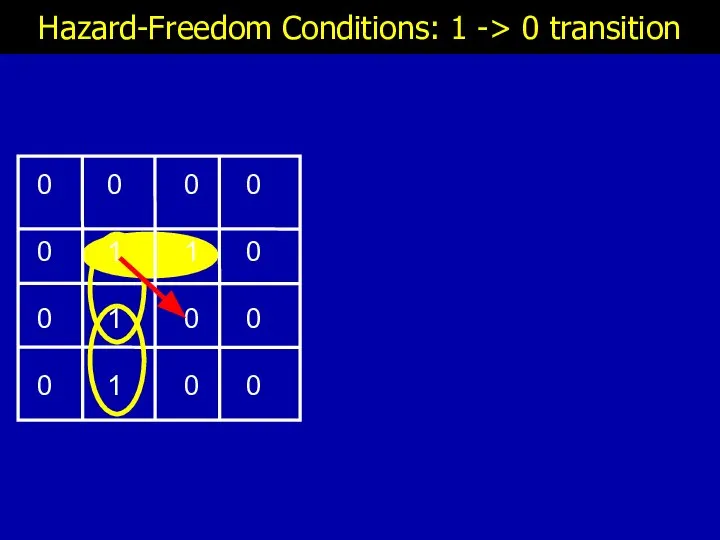
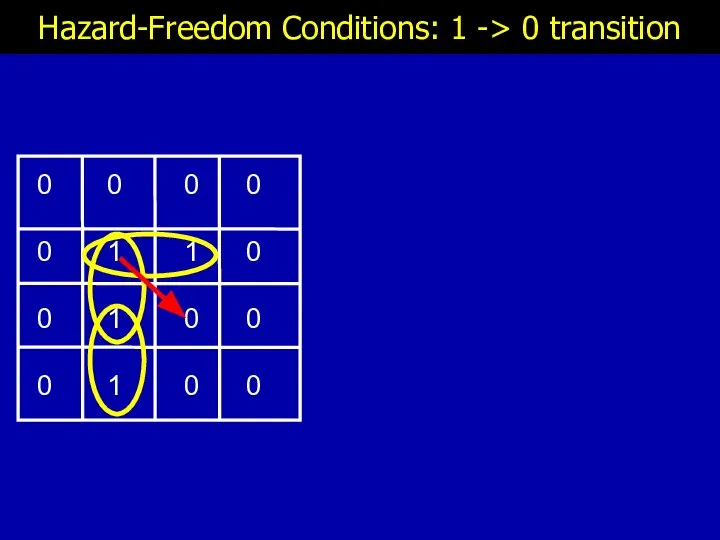
- 12. Hazard-Freedom Conditions: 1 -> 0 transition
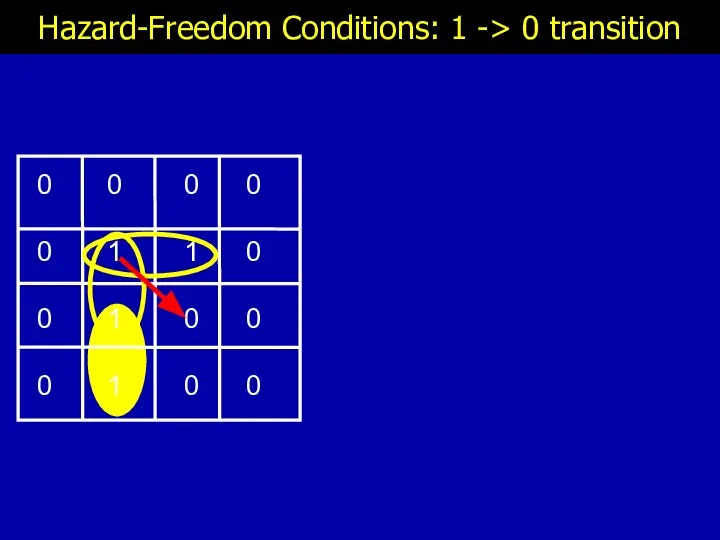
- 13. Hazard-Freedom Conditions: 1 -> 0 transition
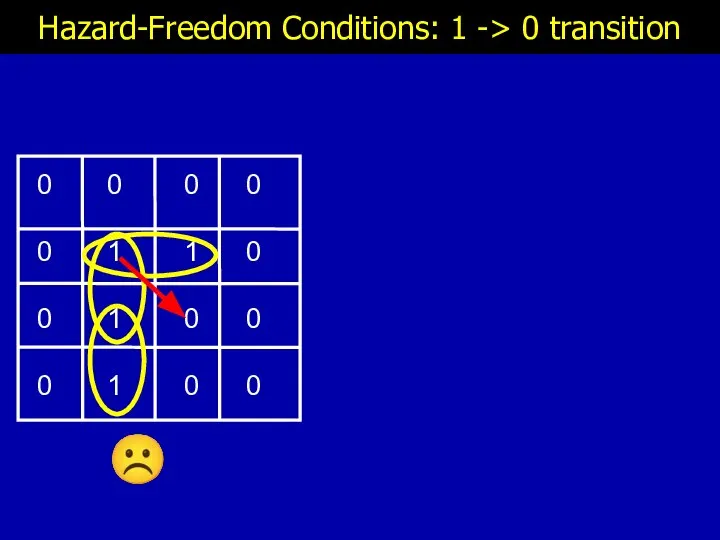
- 14. Hazard-Freedom Conditions: 1 -> 0 transition
- 15. Hazard-Freedom Conditions: 1 -> 0 transition
- 16. Hazard-Freedom Conditions: 1 -> 0 transition
- 17. Hazard-Freedom Conditions: 1 -> 0 transition ☹
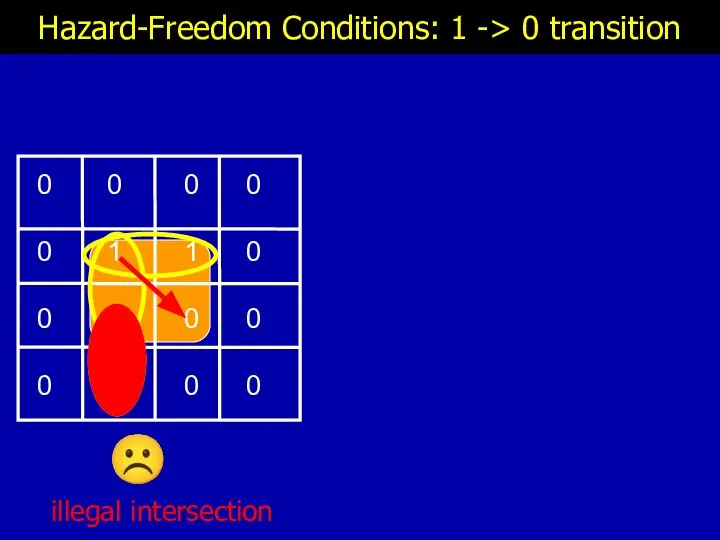
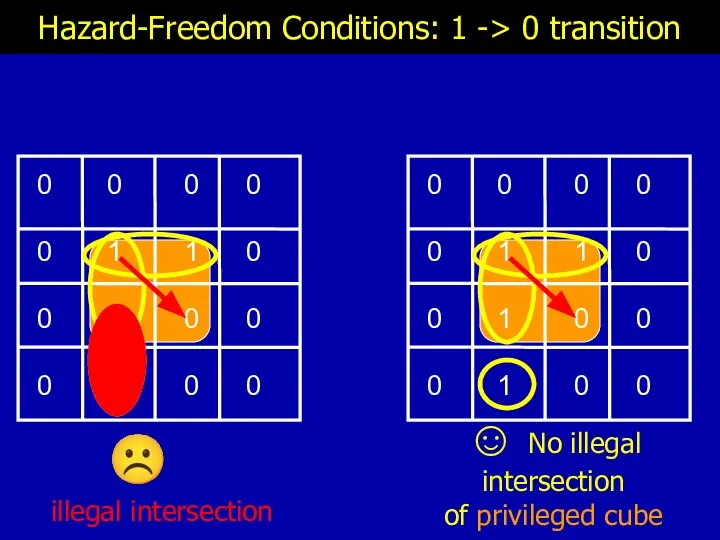
- 18. Hazard-Freedom Conditions: 1 -> 0 transition ☹ illegal intersection
- 19. Hazard-Freedom Conditions: 1 -> 0 transition ☺ No illegal intersection of privileged cube ☹ illegal intersection
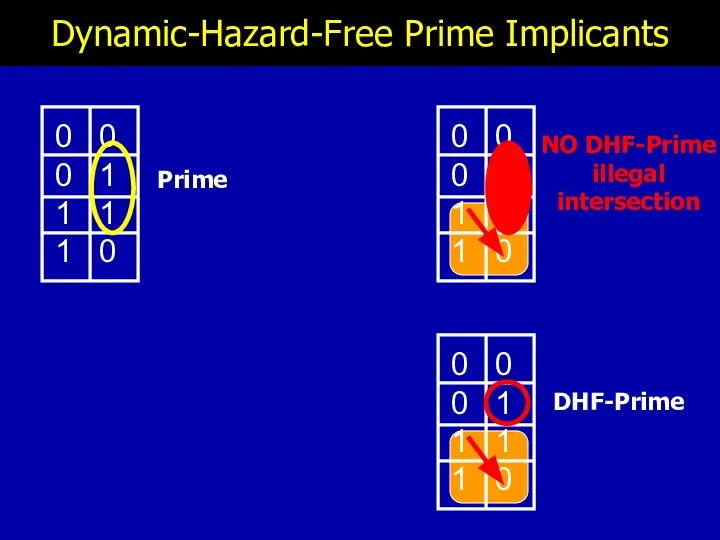
- 20. Dynamic-Hazard-Free Prime Implicants Prime NO DHF-Prime illegal intersection
- 21. 2-level Logic Minimization: Classic vs. Hazard-Free Classic (Quine-McCluskey): Hazard-Free: Given: Boolean function & set of “multi-input”
- 22. Hazard-Free 2-level Logic Minimization: Previous Work Early work (1950s-1970s): Eichelberger, Unger, Beister, McCluskey Initial solution: Nowick/Dill
- 23. IMPYMIN: an exact 2-level minimizer Two main ideas: novel reformulation of hazard-freedom constraints used for dhf-prime
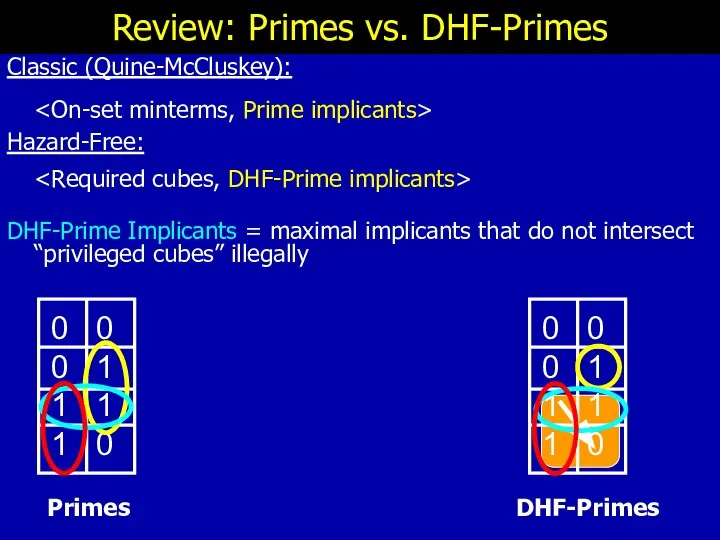
- 24. Review: Primes vs. DHF-Primes Classic (Quine-McCluskey): Hazard-Free: DHF-Prime Implicants = maximal implicants that do not intersect
- 25. Topic 1: New Idea Challenge: Two types of constraints maximality constraints: “we want maximally large implicants”
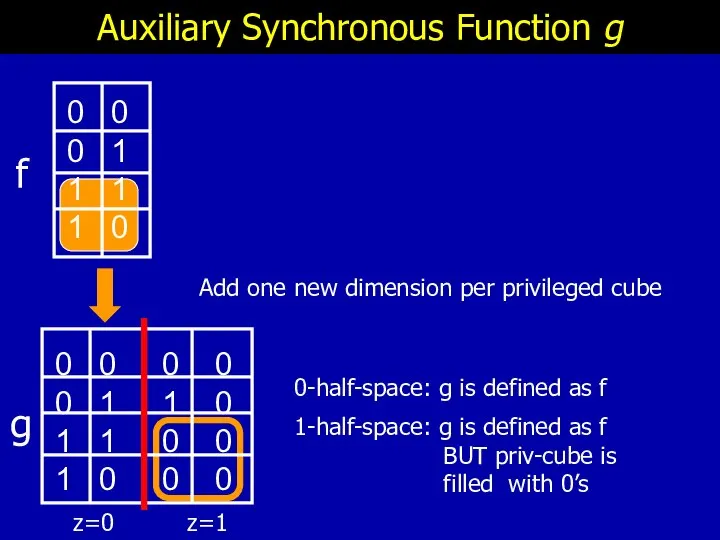
- 26. Auxiliary Synchronous Function g 0 0 0 1 1 1 1 0 0 0 1 0
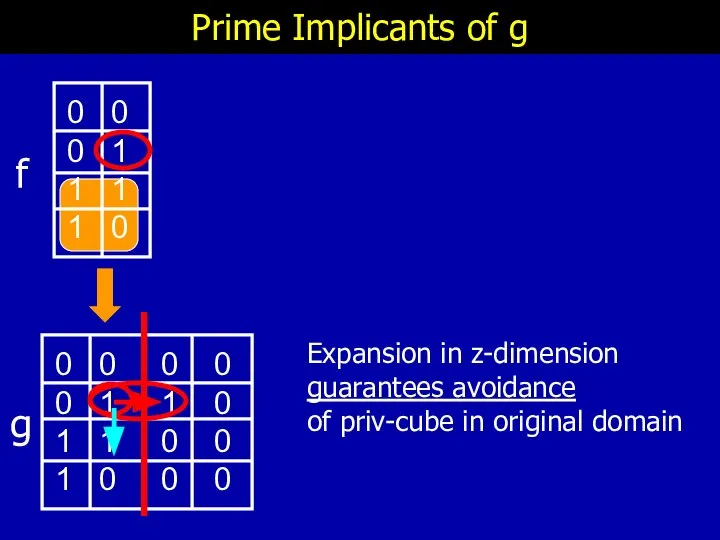
- 27. Prime Implicants of g Expansion in z-dimension guarantees avoidance of priv-cube in original domain f g
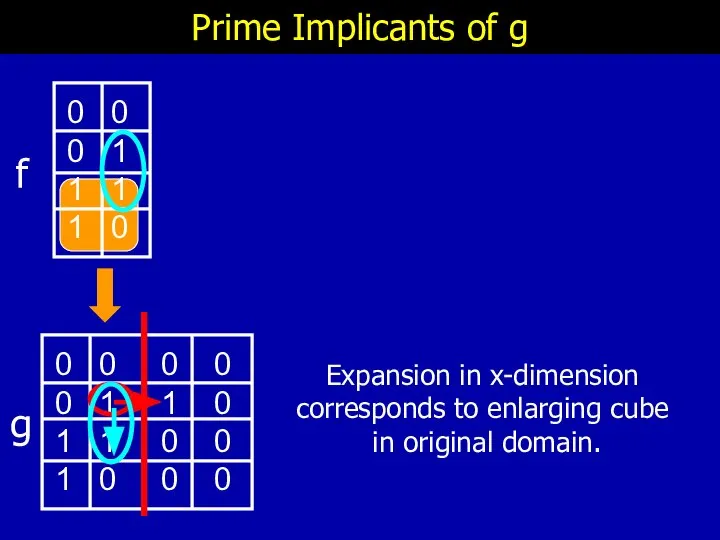
- 28. Prime Implicants of g Expansion in x-dimension corresponds to enlarging cube in original domain. f g
- 29. Summary: Auxiliary Synchronous Function g The definition of auxiliary function g exactly ensures : Expansion in
- 30. New approach: DHF-Prime Generation Goal: Efficient new method for DHF-Prime generation Approach: translate original function f
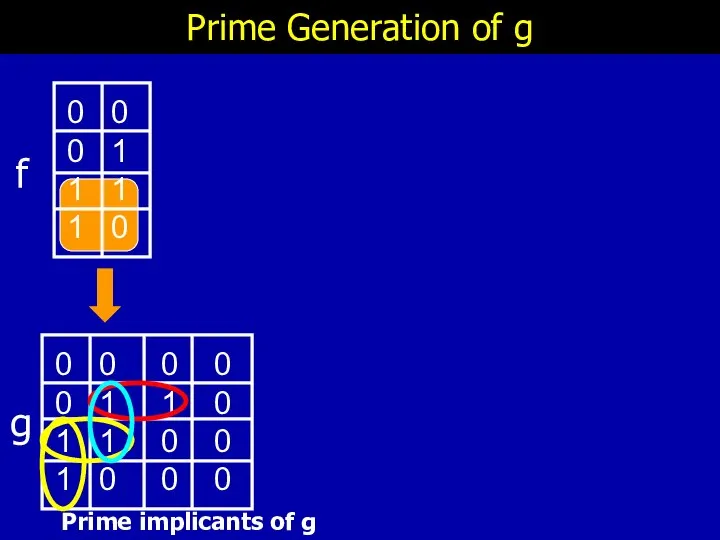
- 31. Prime Generation of g f g Prime implicants of g
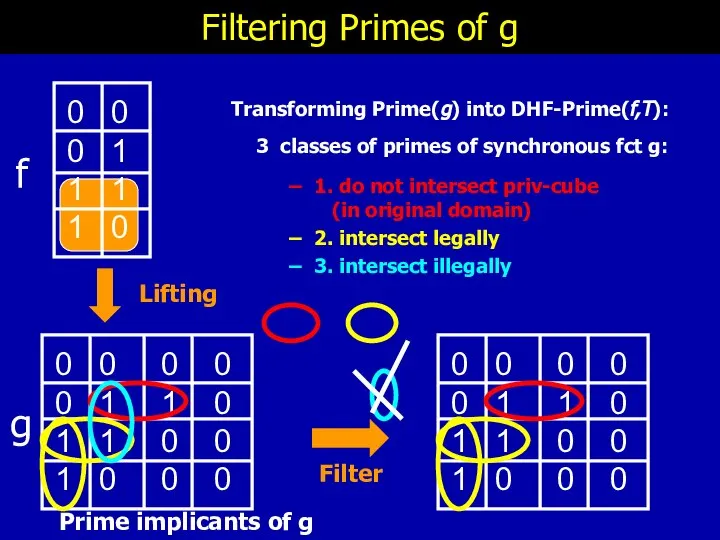
- 32. Filtering Primes of g Lifting Prime implicants of g 3 classes of primes of synchronous fct
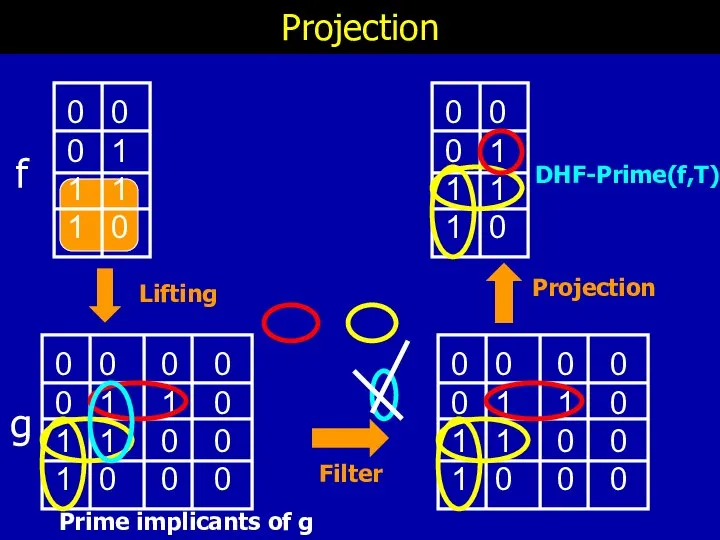
- 33. Projection Lifting Prime implicants of g f g DHF-Prime(f,T)
- 34. Formal Characterization of DHF-Prime(f,T)
- 35. IMPYMIN CAD tool for Hazard-Free 2-Level Logic Two main ideas: Computes DHF-Primes in higher-dimension space Implicit
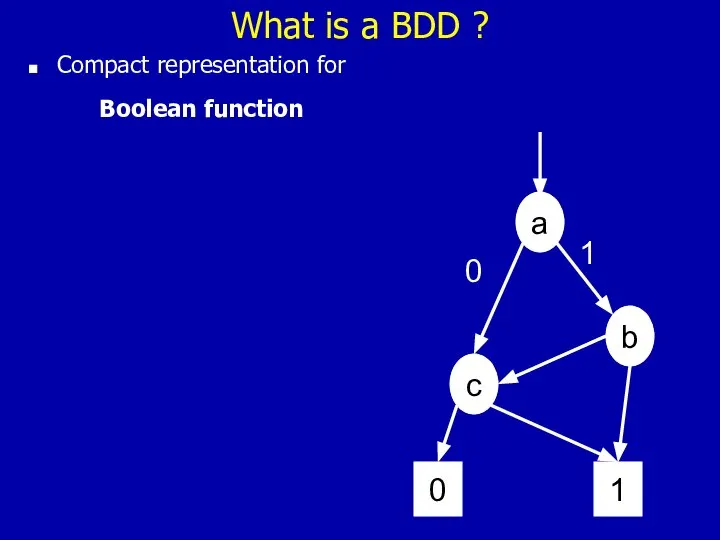
- 36. What is a BDD ? Compact representation for Boolean function a b c 0 1 0
- 37. What is implicit logic minimization? Classic Quine-McCluskey: Scherzo [Coudert] (implicit logic minimization): ?
- 38. IMPYMIN Overview: Implicit Hazard-free 2-Level Minimizer f, T Scherzo’s Implicit Solver objects-to-be-covered covering objects
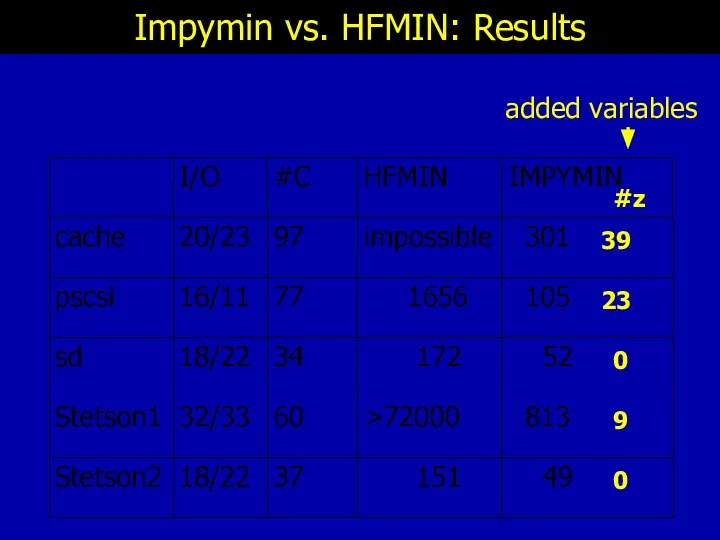
- 39. Impymin vs. HFMIN: Results 39 23 0 9 0 #z added variables
- 41. Скачать презентацию













![What is implicit logic minimization? Classic Quine-McCluskey: Scherzo [Coudert] (implicit logic minimization): ?](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1094263/slide-36.jpg)

 Отсортированная матрица
Отсортированная матрица Основы скетчноутинга
Основы скетчноутинга Организация сетевого взаимодействия участников образовательного процесса ДОУ в социальной сети Instagram
Организация сетевого взаимодействия участников образовательного процесса ДОУ в социальной сети Instagram Продающий или непродающий
Продающий или непродающий Нанотехнологии в космосе, информационные технологии
Нанотехнологии в космосе, информационные технологии Правила безопасного пользования интернетом
Правила безопасного пользования интернетом Форматирование текста (шрифт)
Форматирование текста (шрифт) Факторы, влияющие на надежность аппаратно-программного комплекса
Факторы, влияющие на надежность аппаратно-программного комплекса Рекурсивные алгоритмы. Подготовка к ЕГЭ, задание 11
Рекурсивные алгоритмы. Подготовка к ЕГЭ, задание 11 Форум для девушек Чувства собственного достоинства
Форум для девушек Чувства собственного достоинства Презентация на тему Основы моделирования
Презентация на тему Основы моделирования  Компьютерная графика
Компьютерная графика Чемоданчики Граня
Чемоданчики Граня Технические новинки первой мировой войны
Технические новинки первой мировой войны Глава 2. Компьютер как универсальное устройство для работы с информацией. Тема 2.1. Основные компоненты компьютера и их функции
Глава 2. Компьютер как универсальное устройство для работы с информацией. Тема 2.1. Основные компоненты компьютера и их функции Поисковые системы
Поисковые системы Основные элементы программирования
Основные элементы программирования Объектно-ориентированные технологии программирования и стандарты проектирования
Объектно-ориентированные технологии программирования и стандарты проектирования Правила охраны труда и гигиены работы на компьютере
Правила охраны труда и гигиены работы на компьютере Носители_и_современность
Носители_и_современность Обновление содержания экологического образования в эпоху цифровизации
Обновление содержания экологического образования в эпоху цифровизации Select boot device Sandisk
Select boot device Sandisk Автоматизированные системы контроля деформаций и смещений
Автоматизированные системы контроля деформаций и смещений Деректер қоры
Деректер қоры Нейросети. Создание приложения с помощью нейросетей
Нейросети. Создание приложения с помощью нейросетей Портфолио. Возможности vKонтакте
Портфолио. Возможности vKонтакте Сайт Coca-Cola, правки
Сайт Coca-Cola, правки Информационно-аналитическая деятельность
Информационно-аналитическая деятельность