Содержание
- 2. Содержание Примечания: Z – линейная функция переменных, определяющих искомую вероятность, f(Z) – функция плотности распределения Введение
- 3. Модели двоичного выбора Примеры Типы Метод оценки Функция вероятности события Часто интересны факторы, определяющие подобные ситуации:
- 4. Содержание Примечания: Z – линейная функция переменных, определяющих искомую вероятность, f(Z) – функция плотности распределения Введение
- 5. Логит-модель. Области применения Примечания: Z – линейная функция переменных, определяющих искомую вероятность, f(Z) – функция плотности
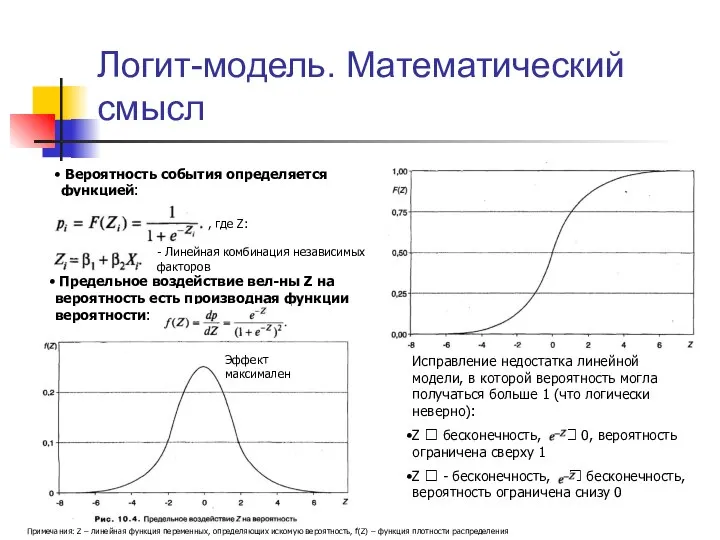
- 6. Логит-модель. Математический смысл Примечания: Z – линейная функция переменных, определяющих искомую вероятность, f(Z) – функция плотности
- 7. Логит-модель. Этапы оценки. Примечания: Z – линейная функция переменных, определяющих искомую вероятность, f(Z) – функция плотности
- 8. Пример. Окончание средней школы (1) Примечания: Z – линейная функция переменных, определяющих искомую вероятность, f(Z) –
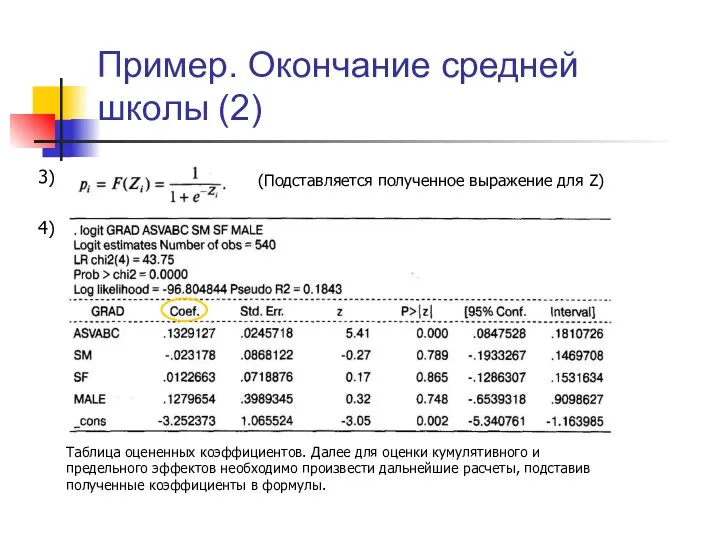
- 9. Пример. Окончание средней школы (2) (Подставляется полученное выражение для Z) 3) 4) Таблица оцененных коэффициентов. Далее
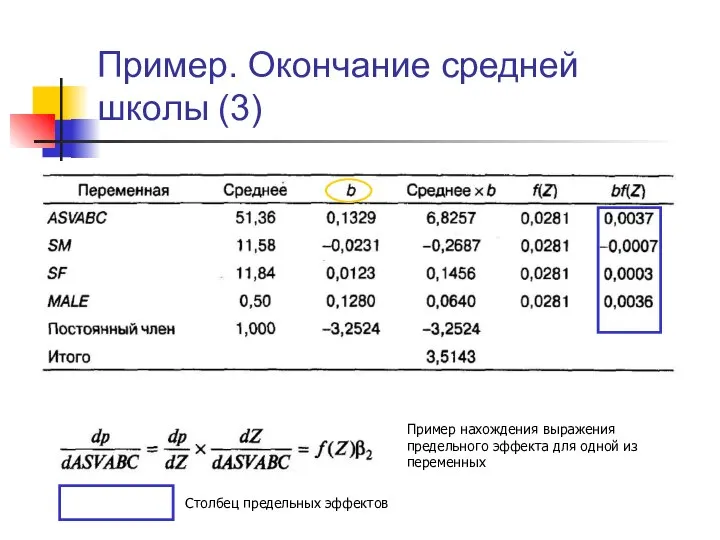
- 10. Пример. Окончание средней школы (3) Пример нахождения выражения предельного эффекта для одной из переменных Столбец предельных
- 11. Пример. Окончание средней школы (4) 5) Увеличение ASVABC на один балл увеличивает вероятность успешного окончания школы
- 12. Пример. Окончание средней школы (4) 6) Для метода максимального правдоподобия нет коэффициента, аналогичного R-square, поэтому используются
- 13. Содержание Примечания: Z – линейная функция переменных, определяющих искомую вероятность, f(Z) – функция плотности распределения Введение
- 14. Пробит-модель. Обзор 1935 год – Chester Bliss «THE CALCULATION OF THE DOSAGE-MORTALITY CURVE», Annals of Applied
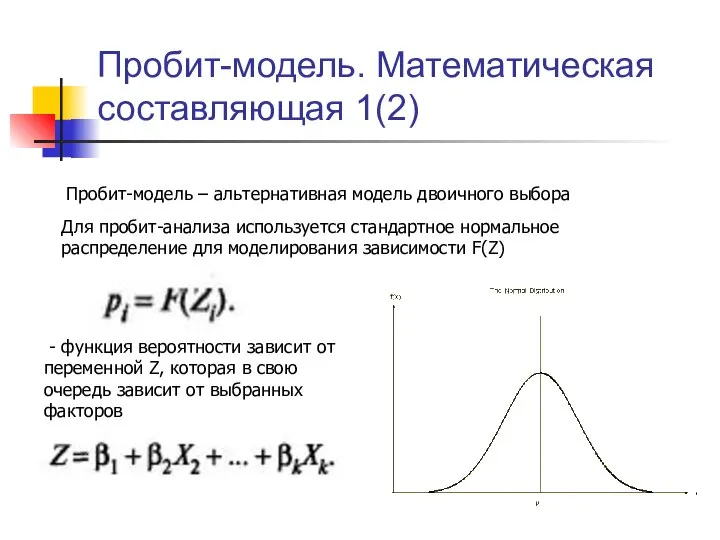
- 15. Пробит-модель. Математическая составляющая 1(2) Пробит-модель – альтернативная модель двоичного выбора Для пробит-анализа используется стандартное нормальное распределение
- 16. Пробит-модель. Математическая составляющая 2(2) Примечания: Z – линейная функция переменных, определяющих искомую вероятность, f(Z) – функция
- 17. Пробит-модель Примечания: Z – линейная функция переменных, определяющих искомую вероятность, f(Z) – функция плотности распределения Расчет
- 18. Пробит-модель. Применение 1(3) Примечания: Z – линейная функция переменных, определяющих искомую вероятность, f(Z) – функция плотности
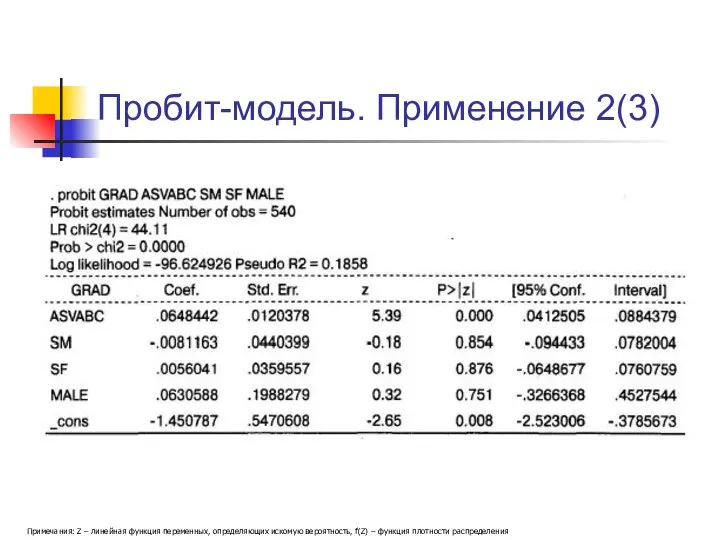
- 19. Пробит-модель. Применение 2(3) Примечания: Z – линейная функция переменных, определяющих искомую вероятность, f(Z) – функция плотности
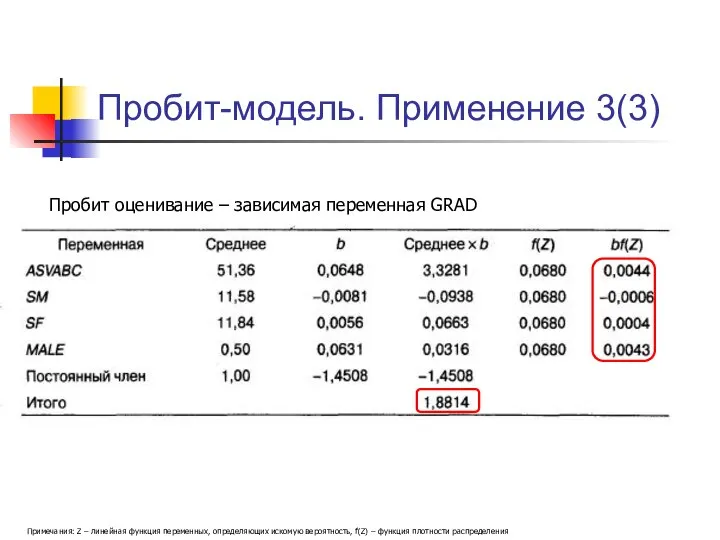
- 20. Пробит-модель. Применение 3(3) Пробит оценивание – зависимая переменная GRAD Примечания: Z – линейная функция переменных, определяющих
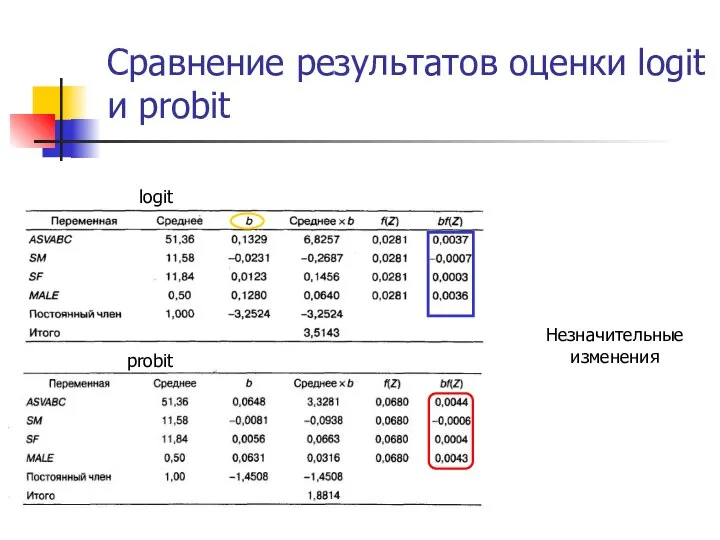
- 21. Сравнение результатов оценки logit и probit Незначительные изменения
- 22. Логит и пробит анализ. Преимущества и недостатки Плюсы Исправление недостатка линейной модели, в которой вероятность могла
- 23. Реальные исследования 1(2) 2010 – «Predicting Foreign Bank Exits? Logit and Probit Regression Approach», Aneta Hryckiewicz
- 24. Реальные исследования. Результаты 2(2) Основная причина закрытия зарубежных отделений – не низкие финансовые показатели филиала, а
- 25. Конец Спасибо за внимание!
- 27. Скачать презентацию

















 Массивы. Работа с массивами
Массивы. Работа с массивами Возможно ли создавать игры с телефона?
Возможно ли создавать игры с телефона? Компьютерные программы, используемые при автоматизации работы парикмахерских и салонов красоты
Компьютерные программы, используемые при автоматизации работы парикмахерских и салонов красоты Компьютерные вирусы
Компьютерные вирусы Язык HTML. Оформление текста
Язык HTML. Оформление текста Алмасу хаттамалары
Алмасу хаттамалары Задачи по теме Алгоритмы и исполнители ОГЭ. Пример 5: Исполнитель Черепашка
Задачи по теме Алгоритмы и исполнители ОГЭ. Пример 5: Исполнитель Черепашка Программирование. Лекция 5
Программирование. Лекция 5 Язык HTML
Язык HTML АО ТомскНИПИнефть: Работа в специнституте ГИС-автоматизации
АО ТомскНИПИнефть: Работа в специнституте ГИС-автоматизации Современные инструменты для разработки и проектирования цифровой части ПС
Современные инструменты для разработки и проектирования цифровой части ПС 2_C_to_CPP
2_C_to_CPP Решение для выгрузки отчетности ПИФ в формате XBRL
Решение для выгрузки отчетности ПИФ в формате XBRL Каскадные таблицы стилей CSS
Каскадные таблицы стилей CSS К Дню победы. Шаблон сайта
К Дню победы. Шаблон сайта Моделирование экспертных систем. Особенности и признаки интеллектуальности информационных систем
Моделирование экспертных систем. Особенности и признаки интеллектуальности информационных систем Компьютерные вирусы и антивирусные программы
Компьютерные вирусы и антивирусные программы Аттестационная работа. Эффективность использования ИКТ
Аттестационная работа. Эффективность использования ИКТ Telegram-бот Медицинский консультант
Telegram-бот Медицинский консультант Установка, настройка и управление службами удалённого доступа
Установка, настройка и управление службами удалённого доступа Вероятностно-временные характеристики приоритетного режима канального уровня протокола Wi-Fi
Вероятностно-временные характеристики приоритетного режима канального уровня протокола Wi-Fi Электронная система голосований
Электронная система голосований Презентация на тему Компьютерная графика
Презентация на тему Компьютерная графика 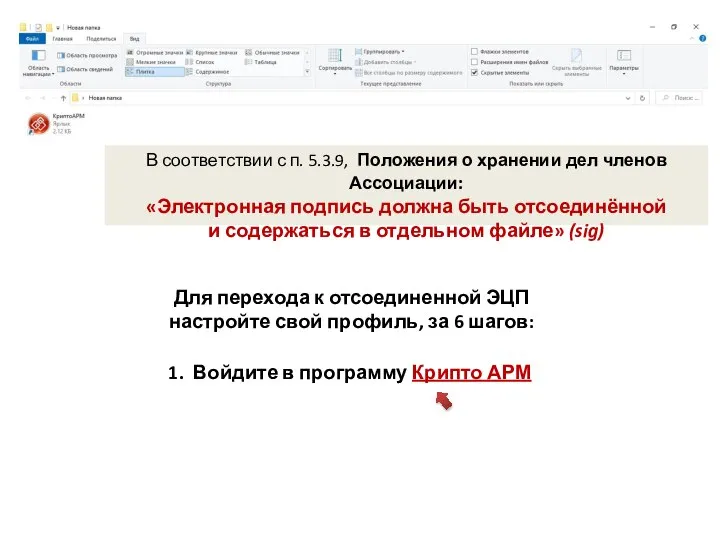 Электронная подпись должна быть отсоединённой и содержаться в отдельном файле
Электронная подпись должна быть отсоединённой и содержаться в отдельном файле Проект по информатике
Проект по информатике Управление персоналом. Правила подготовки докладов в Power Point
Управление персоналом. Правила подготовки докладов в Power Point Базис трехмерного моделирования в программе компас-3D
Базис трехмерного моделирования в программе компас-3D Что мы знаем о компьютере (3 класс)
Что мы знаем о компьютере (3 класс)