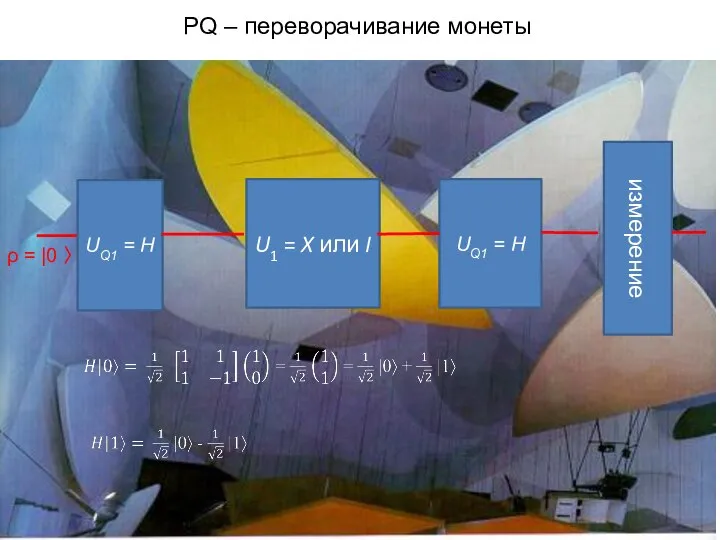
ее (F), либо нет (N)
затем P либо переворачивает монету (F) либо нет (N)
и наконец Q делает финальный ход либо переворачивая монету (F) либо нет (N)
Если в конце монета лежит орлом вверх, то выигрывает P с выигрышем +1, а проигрыш Q составляет -1. В противном случае Q получает +1, а P получает -1.
Матрица выигрышей
Q NN NF FN FF
P:N (−1, +1) (+1, −1) (+1, −1) (−1, +1)
P:F (+1, −1) (−1, +1) (−1, +1) (+1, −1)
Q применяет квантовую стратегию
P обречен на классическую стратегию
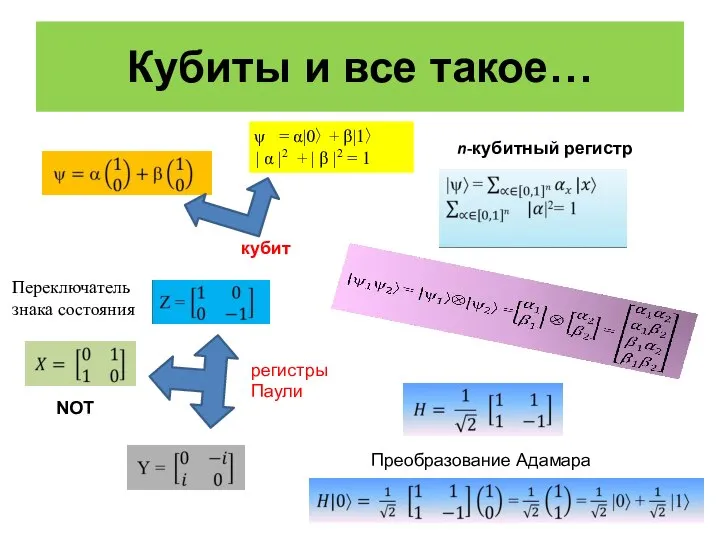
|0〉 - орел
|1〉 - решка
состояние игры представляется кубитом ψ = α|0〉 + β|1〉
начальное состояние игры ρ = |0 〉
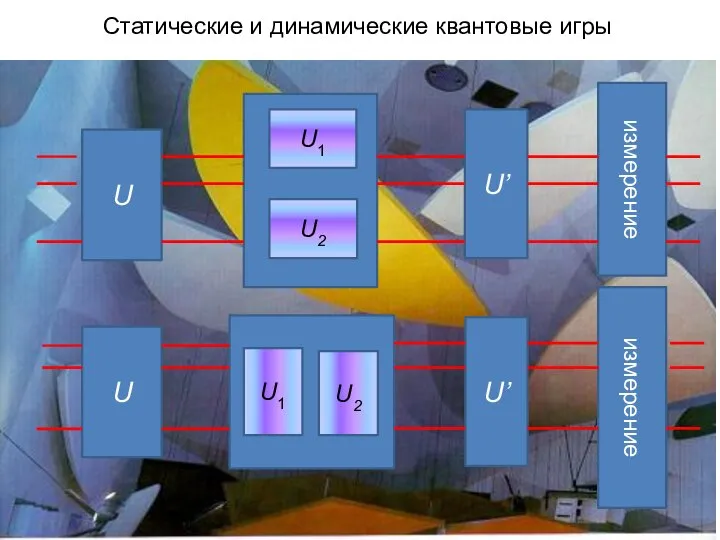
первый ход – тождественное преобразование U
переворачивание F и непереворачивание N представляются преобразованиями X и I соответственно
P может сыграть либо X, либо I, а Q может выбрать любое унитарное преобразование (используется преобразование Адамара)
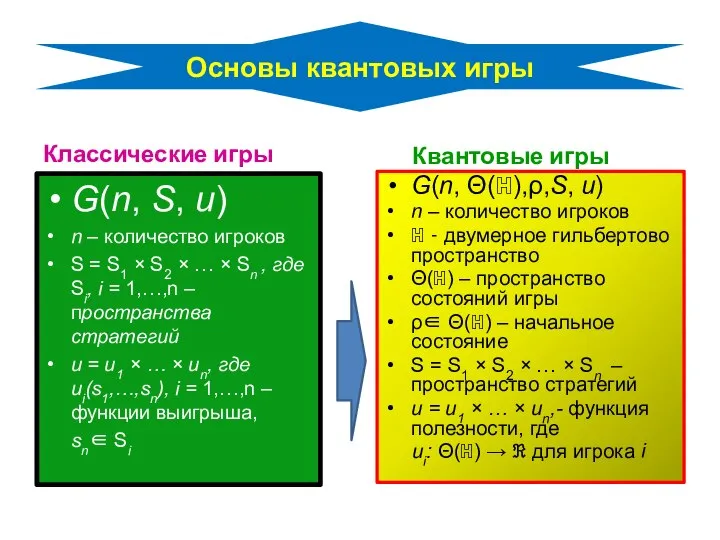
игра характеризуется как
G(n = 2,Θ(ℍ) = ℍ,ρ = |0 〉,S1×S2,,u)
S1 = {X,I}, S2 есть множество всех унитарных матриц
U совпадает с классическим случаем



![Логика Дишканта LQ Г.Дишкант [1978] предложил включить аксиомы Макки в исчисление Лукасевича](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1051610/slide-8.jpg)




 Lektsia_4_Elementy_upravlenia
Lektsia_4_Elementy_upravlenia Миссия Qrnps. Приглашение к сотрудничеству
Миссия Qrnps. Приглашение к сотрудничеству Презентация на тему Кодирование информации с помощью знаковых систем
Презентация на тему Кодирование информации с помощью знаковых систем  Web Flow Inc - программное обеспечение в качестве услуги для создания веб-сайтов и хостинга
Web Flow Inc - программное обеспечение в качестве услуги для создания веб-сайтов и хостинга Информационная открытость как индикатор доступности предоставления социальных услуг
Информационная открытость как индикатор доступности предоставления социальных услуг Группы подписчиков магазина БАДов
Группы подписчиков магазина БАДов Символьные переменные. Итоговый урок
Символьные переменные. Итоговый урок Создание комикса с помощью современных технологий
Создание комикса с помощью современных технологий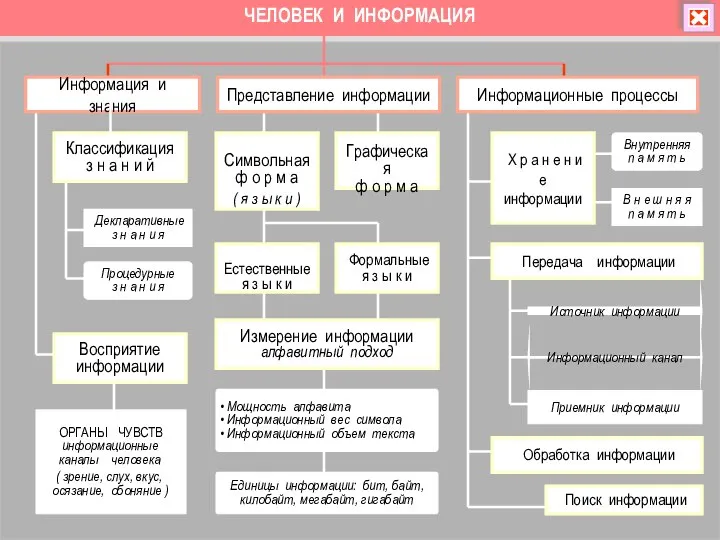 Человек и информация. Информация и знания
Человек и информация. Информация и знания Растровая и векторная графика
Растровая и векторная графика Технологии и опыт мирового уровня в области системной интеграции и разработки программного обеспечения
Технологии и опыт мирового уровня в области системной интеграции и разработки программного обеспечения Введение в C++. Философия C++
Введение в C++. Философия C++ Группа кск Пегас(ролевая). Чемпионат мира
Группа кск Пегас(ролевая). Чемпионат мира Кейс: сравнительный анализ НЛМК и Северсталь
Кейс: сравнительный анализ НЛМК и Северсталь Разветвляющиеся вычислительные процессы
Разветвляющиеся вычислительные процессы RRDesk ver.8
RRDesk ver.8 Системы программирования
Системы программирования Новый сайт Центрального Сибирского геологического музея
Новый сайт Центрального Сибирского геологического музея Представление информации
Представление информации Инструмент для НТ Gatling
Инструмент для НТ Gatling Архитектура, назначение и функции операционных систем. Введение в теорию операционных систем. Занятие 1.1
Архитектура, назначение и функции операционных систем. Введение в теорию операционных систем. Занятие 1.1 Интеллектуальная игра: алфавит
Интеллектуальная игра: алфавит Построение графика функции в MS Excel
Построение графика функции в MS Excel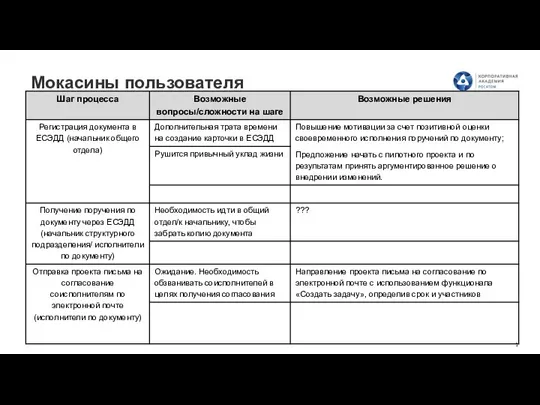 Мокасины пользователя
Мокасины пользователя Оформление списка литературы
Оформление списка литературы Компьютерные вирусы
Компьютерные вирусы Режимы передачи данных
Режимы передачи данных Триггеры в презентации. Применение. Создание слайдов с триггерами
Триггеры в презентации. Применение. Создание слайдов с триггерами