таких пар чисел i и j, что i < j и A[i] > A[j].
Решение:
Заведём массив B размера Amax + 1, где Amax равно максимально возможному значению элемента массива А, и заполним его нулями. Переберём все элементы массива А. Для каждого элемента A[i] будем проставлять значение B[A[i]] равное 1. Тогда при рассмотрении A[i] количество элементов A[j] таких, что i > j и A[i] < A[j], будет равно сумме элементов массива В на отрезке [A[i] + 1; Amax], что является количеством инверсий, в которых меньший элемент – A[i]. Сумма этих сумм и будет являться количеством инверсий всего массива А.
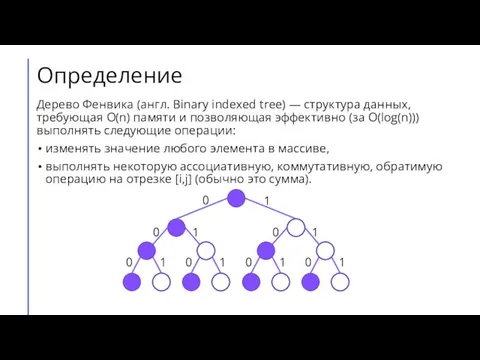
![Принцип работы Для массива A будем хранить массив Т такой, что T[i]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/840846/slide-3.jpg)
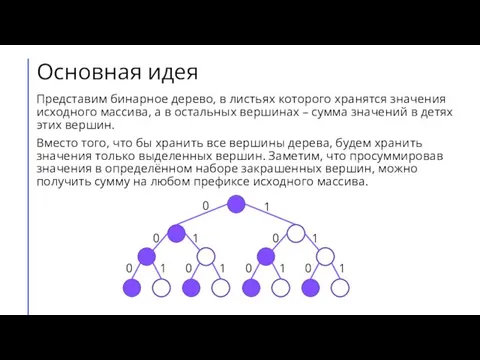
![Принцип работы Для вычисления суммы на отрезке [0; r] массива А нужно](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/840846/slide-4.jpg)






 Информационные системы
Информационные системы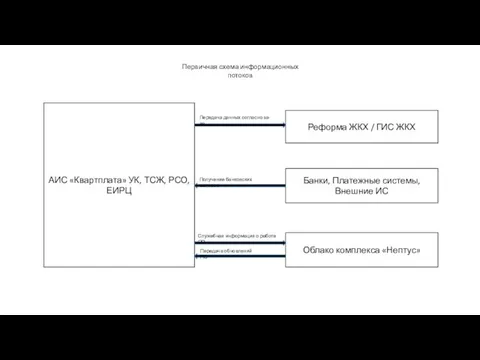 Первичная схема информационных потоков
Первичная схема информационных потоков Построение типовой модели нарушителя безопасности в коммерческой организации
Построение типовой модели нарушителя безопасности в коммерческой организации Ассортиментная идентификация продовольственных товаров
Ассортиментная идентификация продовольственных товаров Составной оператор
Составной оператор Как можно задать значение переменной? Оператор присваивания
Как можно задать значение переменной? Оператор присваивания Презентация на тему Текстовая информация
Презентация на тему Текстовая информация  Математическое моделирование
Математическое моделирование Продающий или непродающий
Продающий или непродающий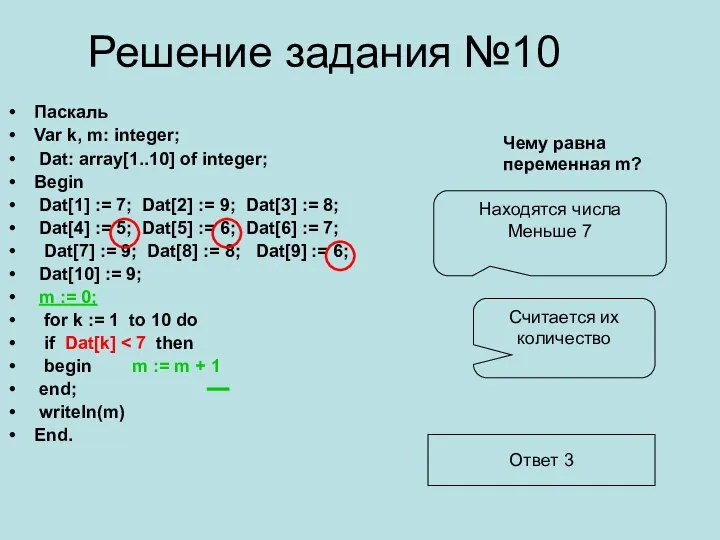 Решение задания №10. Паскаль
Решение задания №10. Паскаль Компьютерные вирусы
Компьютерные вирусы Регистрация и установка программы Adobe Creative Cloud
Регистрация и установка программы Adobe Creative Cloud Гибридные криптосистемы защиты информации
Гибридные криптосистемы защиты информации Графический редактор
Графический редактор Лекция №1.Основные понятия теории баз данных
Лекция №1.Основные понятия теории баз данных Prezentatsia_EVM
Prezentatsia_EVM Архитектура ПК лекция
Архитектура ПК лекция Интенсив. Слепой метод набора
Интенсив. Слепой метод набора Использование ИКТ на уроках изобразительного и декоративно-прикладного искусства
Использование ИКТ на уроках изобразительного и декоративно-прикладного искусства Описание проблемы в СЭД
Описание проблемы в СЭД Витраж. Алгоритм
Витраж. Алгоритм Сборник Adobe Photoshop CS5 для начинающих
Сборник Adobe Photoshop CS5 для начинающих Занятия ОПИ Интернет-промотирование
Занятия ОПИ Интернет-промотирование Что такое токен чата?
Что такое токен чата? Основы ПИКГ. Программы AutoCAD SketchUP
Основы ПИКГ. Программы AutoCAD SketchUP Использование основных методов информатики и средств ИКТ при анализе процессов в обществе, природе и технике
Использование основных методов информатики и средств ИКТ при анализе процессов в обществе, природе и технике Готовимся к экзамену №1. Разбираем типовые ошибки
Готовимся к экзамену №1. Разбираем типовые ошибки Онлайн образование с применением машинного обучения
Онлайн образование с применением машинного обучения