Системы счисления

Системы счисления
§ 1. Кодирование чисел

Что такое система счисления?
Система счисления — это правила записи чисел с помощью специальных знаков — цифр, а также соответствующие правила выполнения операций с этими числами.
Счёт на пальцах:
Унарная (лат. unus – один) – одна цифра обозначает единицу (1 день, 1 камень, 1 баран, …)
только натуральные числа
запись больших чисел – длинная (1 000 000?)

Непозиционные системы счисления
Непозиционная система счисления — это такая система, в которой значение цифры не зависит от её места (позиции) в записи числа.
унарная
египетская десятичная
римская
славянская
и другие…

Египетская десятичная система
– 1
– 10
– 100
– 1000
– 10000
– 100000
– 1000000
черта
хомут
верёвка
лотос
палец
лягушка
человек
= ?
= 1235
2014 = ?

Римская система счисления
I – 1 (палец)
V – 5 (раскрытая ладонь)
X – 10 (две ладони)
L – 50
C – 100 (Centum)
D – 500 (Demimille)
M – 1000 (Mille)
Спасская башня Московского Кремля

Римская система счисления
Правила:
(обычно) не ставят больше трех
одинаковых цифр подряд
если младшая цифра (только одна!) стоит слева от старшей, она вычитается из суммы (частично непозиционная!)
Примеры:
MDCXLIV =
1000
+ 500
+ 100
– 10
+ 50
– 1
+ 5
2389 = 2000 + 300 + 80 + 9
2389 = M M C C C L X X X I X
M M
CCC
LXXX
IX
= 1644

Римская система счисления
MCDLXVII =
MMDCXLIV =
MMMCCLXXII =
CMXXVIII =

Римская система счисления
3768 =
2983 =
1452 =
1999 =

Римская система счисления
только натуральные числа (дробные? отрицательные?)
для записи больших чисел нужно вводить новые цифры
сложно выполнять вычисления

Славянская система счисления
алфавитная система счисления (непозиционная)
Часы Суздальского Кремля

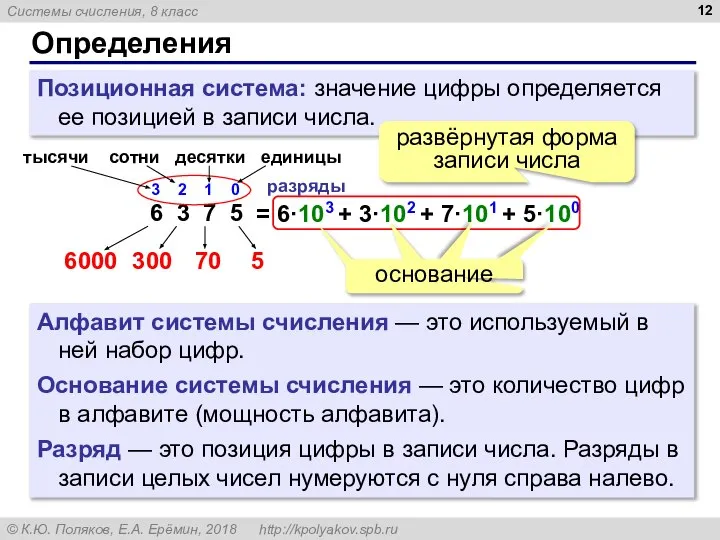
Определения
Позиционная система: значение цифры определяется ее позицией в записи числа.
Алфавит системы счисления — это используемый в ней набор цифр.
Основание системы счисления — это количество цифр в алфавите (мощность алфавита).
Разряд — это позиция цифры в записи числа. Разряды в записи целых чисел нумеруются с нуля справа налево.
6 3 7 5
5
70
300
6000
3 2 1 0
разряды
= 6·103 + 3·102 + 7·101 + 5·100
развёрнутая форма записи числа

Другие позиционные системы
двоичная
восьмеричная
шестнадцатеричная
и другие…
101102
= 1⋅24 + 0⋅23 + 1⋅22 + 1⋅21 + 0⋅20
4 3 2 1 0
= 22
1458
2 1 0
= 1⋅82 + 4⋅81 + 5⋅80
= 101
12316
2 1 0
= 1⋅162 + 2⋅161 + 3⋅160
= 291
1235
2 1 0
= 1⋅52 + 2⋅51 + 3⋅50
= 38
4567
1022
36512
5788
1729
5214

Позиционные системы счисления
Задача. В некоторой системе счисления число 58 записывается как 46x. Определите основание x этой системы счисления.
46x
1 0
= 4⋅x1 + 6⋅x0
4x + 6 = 58
4x = 52
x = 13
= 4x + 6
Переведём 46x в десятичную систему:

Системы счисления
§ 2. Двоичная система
счисления

Двоичная система счисления
Основание (количество цифр): 2
Алфавит: 0, 1
длинная запись чисел: 1024 = 100000000002
запись однородна (только 0 и 1)
нужны только устройства с двумя состояниями
компьютеру проще выполнять вычисления (умножение сводится сложению и т.п.)

Перевод в десятичную систему
2 → 10
100112
4 3 2 1 0
разряды
= 1·24 + 0·23 + 0·22 + 1·21 + 1·20
= 16 + 2 + 1 = 19
10 → 2
Выделение степеней числа 2:
21 = 16 + 5
21 = 1⋅24 + 0⋅23 + 1⋅22 + 0⋅21 + 1⋅20
= 16 + 4 + 1
24
24
22
20
= 101012

Выделение степеней числа 2
10 → 2
77
77 =
64 + 13
8 + 5
4 + 1
1
1
1
1
77 = 10011012

Другой способ
100112
= 1·24 + 0·23 + 0·22 + 1·21 + 1·20
= (1·23 + 0·22 + 0·21 + 1·20)·2 + 1
10012 = 100112 : 2
деление нацело
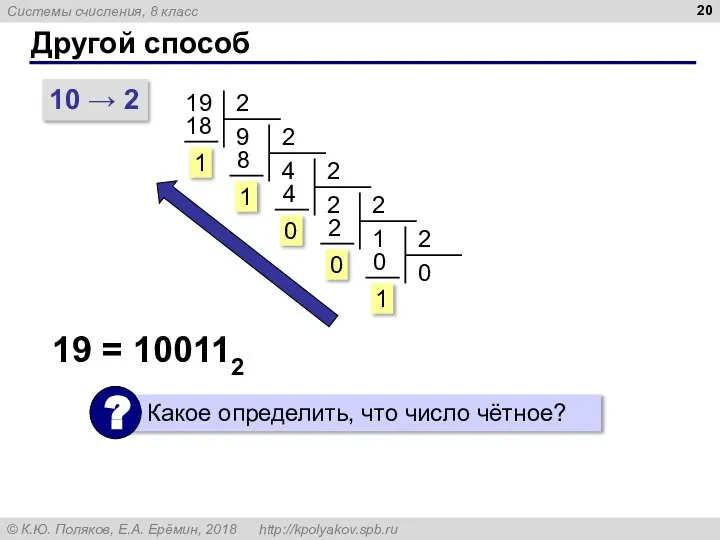
4 3 2 1 0

Другой способ
10 → 2
19
19 = 100112

Сложение в двоичной системе
10
6
5
3
1
1
1
1
2
1 0 1 1 02
+ 1 1 1 0 1 12
1
1
0
0
1
0
1
1
0
2
1
1
1
1 + 1 = 2 = 102
1 + 1 + 1 = 3 = 112

Сложение в двоичной системе

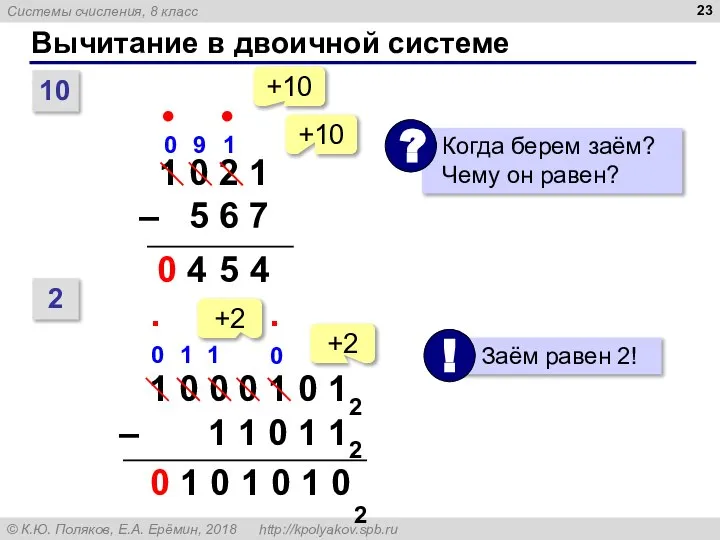
Вычитание в двоичной системе
10
4
5
4
9
•
•
0
2
1
0
+10
+10
1 0 0 0 1 0 12
– 1 1 0 1 12
1
∙
∙
1
0
0
1
0
0
+2
0
1
1
+2

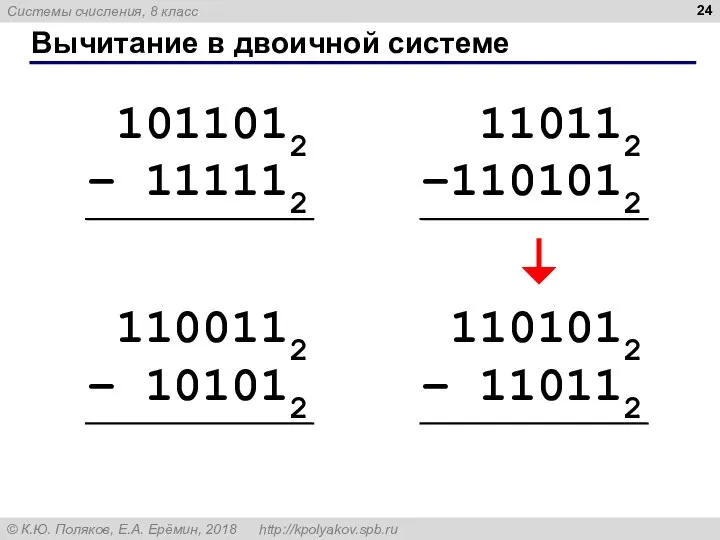
Вычитание в двоичной системе

Системы счисления
§ 3. Восьмеричная система
счисления

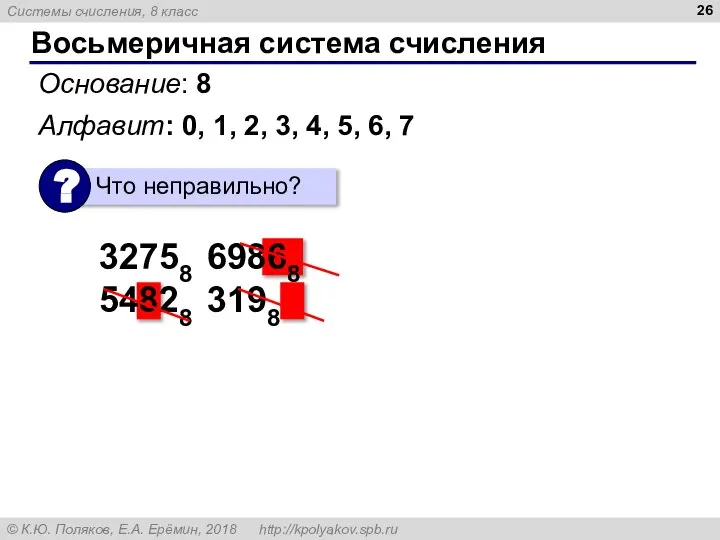
Восьмеричная система счисления
Основание: 8
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7
32758 69868
54828 3198

Из восьмеричной в десятичную
8 → 10
1448
2 1 0
разряды
= 1·82 + 4·81 + 4·80
= 64 + 32 + 4 = 100
Переведите:
128 =
578 =
648 =
778 =
1208
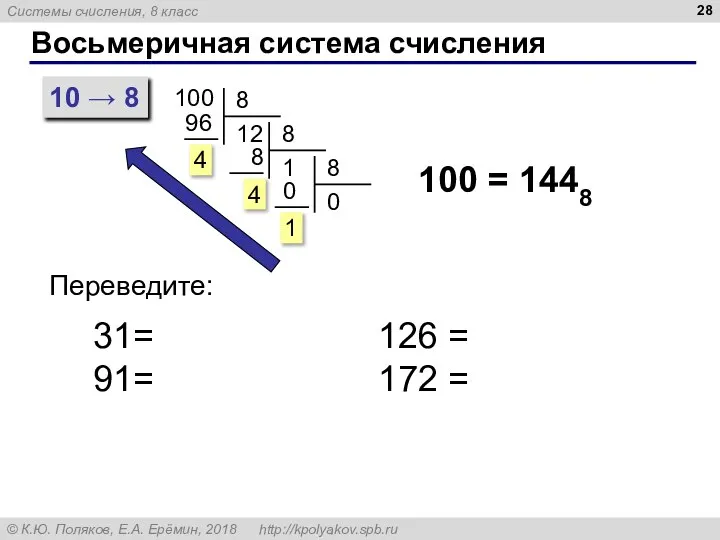
57008

Восьмеричная система счисления
10 → 8
100
100 = 1448
Переведите:
31=
91=
126 =
172 =

Связь с двоичной системой
7538 = 7⋅ 82 + 5⋅81 + 3⋅80
= 7⋅ 26 + 5⋅23 + 3⋅20
7538 = (1⋅ 22 + 1⋅ 21 + 1⋅ 20) ⋅ 26 +
(1⋅ 22 + 0⋅ 21 + 1⋅ 20) ⋅ 23 +
(0⋅ 22 + 1⋅ 21 + 1⋅ 20) ⋅ 20
7538 = 1⋅ 28 + 1⋅ 27 + 1⋅ 26 +
1⋅ 25 + 0⋅ 24 + 1⋅ 23 +
0⋅ 22 + 1⋅ 21 + 1⋅ 20
= 1111010112
8 = 23

Связь с двоичной системой
8 = 23
16258 =
1 6 2 5
001
{
{
110
010
1012
{
{

Перевод из двоичной в восьмеричную
10010111011112
Шаг 1. Разбить на триады, начиная справа:
001 001 011 101 1112
Шаг 2. Каждую триаду записать одной восьмеричной цифрой:
1
3
5
7
Ответ: 10010111011112 = 113578
001 001 011 101 1112
1

Связь с двоичной системой
Переведите в двоичную систему:
3758 =
52468 =
Переведите в восьмеричную систему:
10100112 =
101011002 =

Сжатая запись двоичных кодов
3
6
1368
Запишите в сжатой форме:
PDP-11, ДВК, СМ ЭВМ, БЭСМ, БК
1

Сложение
сложение
1 5 68
+ 6 6 28
1
1
6 + 2 = 8 = 8 + 0
5 + 6 + 1 = 12 = 8 + 4
1 + 6 + 1 = 8 = 8 + 0
1
1 в перенос
1 в перенос
1
08
0
4
1 в перенос

Вычитание
вычитание
4 5 68
– 2 7 78
∙
(6 + 8) – 7 = 7
(5 – 1 + 8) – 7 = 5
(4 – 1) – 2 = 1
∙
заём
78
1
5
заём

Выполните сложение и вычитание

Системы счисления
§ 4. Шестнадцатеричная
система счисления

Шестнадцатеричная система
Основание: 16
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,
A,
10
B,
11
C,
12
D,
13
E,
14
F
15
34AF516 5BG616
9FF6116 ADH2316

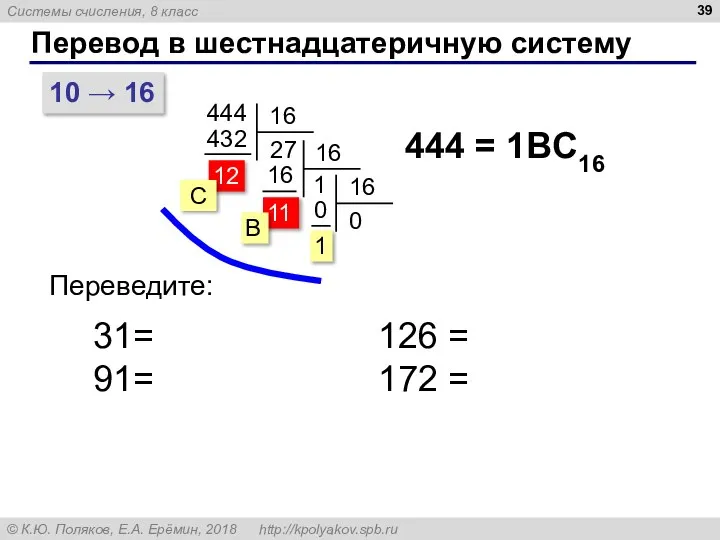
Перевод в шестнадцатеричную систему
11
10 → 16
444
444 = 1BC16
С
B
Переведите:
31=
91=
126 =
172 =

Перевод из шестнадцатеричной системы
16 → 10
1BC16
2 1 0
разряды
= 1·162 + 11·161 + 12·160
= 256 + 176 + 12 = 444
B
C
Переведите:
1216 =
5A16 =
B916 =
AB16 =
12016
570016

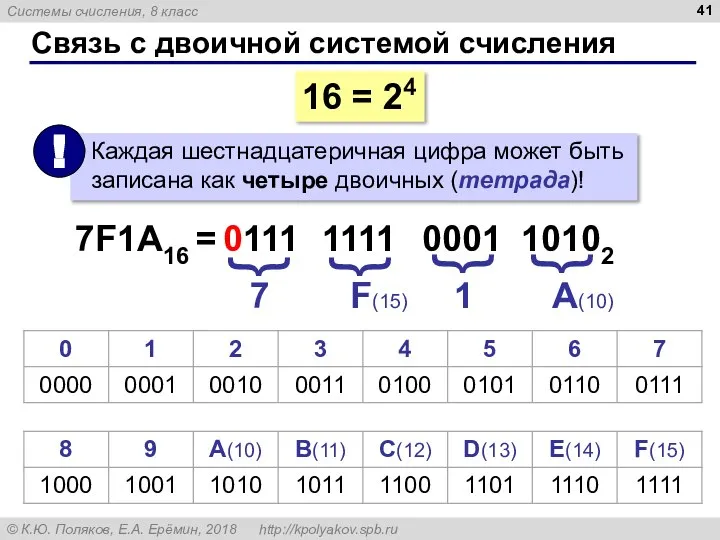
Связь с двоичной системой счисления
16 = 24
7F1A16 =
7 F(15) 1 A(10)
0111
{
{ 1111
0001
10102
{
{

Перевод из двоичной системы
Шаг 1. Разбить на тетрады, начиная справа:
0001 0010 1110 11112
Шаг 2. Каждую тетраду записать одной шестнадцатеричной цифрой:
0001 0010 1110 11112
1
2
E
F
Ответ: 10010111011112 = 12EF16
10010111011112

Сжатая запись двоичных кодов
5
E
5E16
Запишите в сжатой форме:
Intel, AMD, ARM

Сжатая запись двоичных кодов
Закодируйте рисунок и запишите в сжатой форме:

Связь с двоичной системой счисления
Переведите в двоичную систему:
EA123816 =
Переведите в шестнадцатеричную систему :
111110100112 =
Переведите в восьмеричную систему :
2FA16 =
Переведите в шестнадцатеричную систему :
1658 =

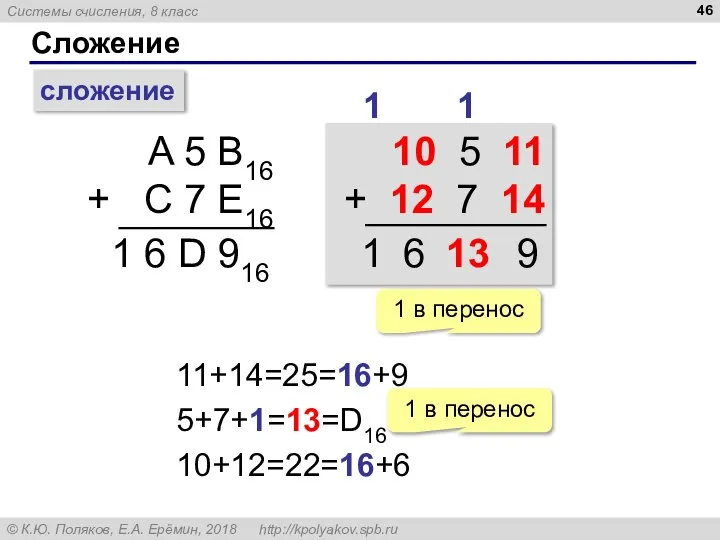
Сложение
сложение
A 5 B16
+ C 7 E16
1
1 6 D 916
10 5 11
+ 12 7 14
11+14=25=16+9
5+7+1=13=D16
10+12=22=16+6
1
1 в перенос
1 в перенос
13
9
6
1

Вычитание
вычитание
С 5 B16
– A 7 E16
заём
∙
1 D D16
12 5 11
– 10 7 14
∙
(11+16)–14=13=D16
(5 – 1)+16 – 7=13=D16
(12 – 1) – 10 = 1
заём
13
1
13

Арифметические действия
1 В А16
– A 5 916
С В А16
+ A 5 916

Конец фильма
ПОЛЯКОВ Константин Юрьевич
д.т.н., учитель информатики
ГБОУ СОШ № 163, г. Санкт-Петербург
[email protected]
ЕРЕМИН Евгений Александрович
к.ф.-м.н., доцент кафедры мультимедийной дидактики и ИТО ПГГПУ, г. Пермь
[email protected]