Доказательство правильности программ. Структурное программирование

Пример использования структурного программирования
Структу́рное программи́рование — методология разработки программного
обеспечения, в основе которой лежит представление программы в виде
иерархической структуры блоков. Предложена в 1970-х годах Э. Дейкстрой
Структурное программирование:
Проектирование сверху вниз
Функциональное программирование
Структурное кодирование
Задача нахождения НОД.
I. Общая постановка: даны целые a и b, найти их НОД.
Пусть a и b ≠ 0 и есть НОД(a,b). Ноль делится на любое число, поэтому НОД(0, 0) = 0 и
НОД(u, v) = НОД(v, u) и
НОД(u, v) = НОД (-u, v) и
НОД(u, 0) = u
II. Даны целые, неотрицательные a и b, найти их НОД.
Проведем декомпозицию этой задачи. Предположим, что можно привести задачу нахождения НОД(a,b) для b > 0, к задаче нахождения НОД(x,y), где x и y тоже неотрицательные и y < b. Тогда после выполнения такого преобразования конечное число раз, придем к ситуации, когда y = 0. С учетом соотношений получим
НОД(a, b) = НОД (x, y) = x

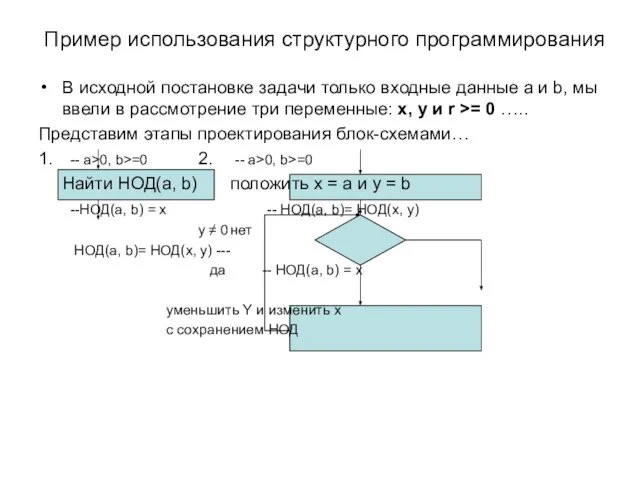
Пример использования структурного программирования
Декомпозиция на три подзадачи:
положить x = a и y = b
если y ≠ 0, то а) уменьшить y и изменить x так, чтобы x и y оставались >= 0, и чтобы значение НОД(x,y) оставалось тем же. b) повторить второй этап
если y = 0, положить НОД(a,b) = x
Первая и третья задача уже достаточно просты, а вторая …решена Евклидом:
III. Если (x div y) – целая часть, а (x mod y) – остаток, то x = (x div y) * y + (x mod y)
и если x и y делятся на какое-то число, то на это число будет делиться y и x – (x div y) * y, то есть y и (x mod y)
и НОД(x, y) = НОД(y, x mod y),
так как (x mod y) < y, эти рассуждения показывают как «уменьшить» y и «изменить» x во второй подзадаче. Алгоритм:
1) положить x = a и y = b
если y ≠ 0, то
а) установить r = x mod y b) положить x = y с) положить y = r. d) повторить второй этап
3) если y = 0, положить НОД(a,b) = x

Пример использования структурного программирования
В исходной постановке задачи только входные данные a и b, мы ввели в рассмотрение три переменные: x, y и r >= 0 …..
Представим этапы проектирования блок-схемами…
1. -- a>0, b>=0 2. -- a>0, b>=0
Найти НОД(a, b) положить x = a и y = b
--НОД(a, b) = x -- НОД(a, b)= НОД(x, y)
y ≠ 0 нет
НОД(a, b)= НОД(x, y) ---
да -- НОД(a, b) = x
уменьшить Y и изменить x
с сохранением НОД

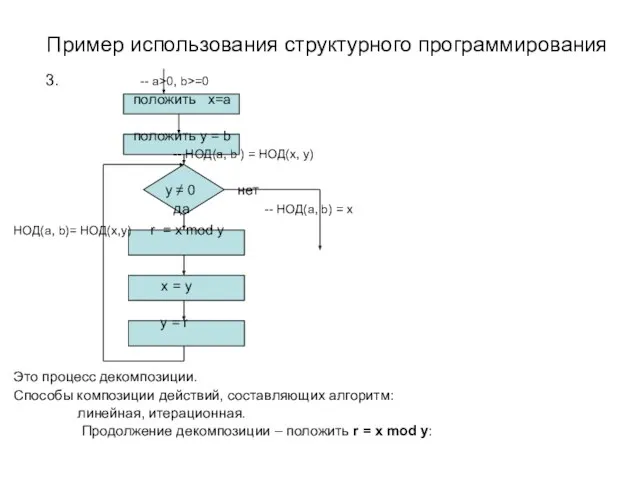
Пример использования структурного программирования
3. -- a>0, b>=0
положить x=a
положить y = b
-- НОД(a, b ) = НОД(x, y)
y ≠ 0 нет
да -- НОД(a, b) = x
НОД(a, b)= НОД(x,y) r = x mod y
x = y
y = r
Это процесс декомпозиции.
Способы композиции действий, составляющих алгоритм:
линейная, итерационная.
Продолжение декомпозиции – положить r = x mod y:

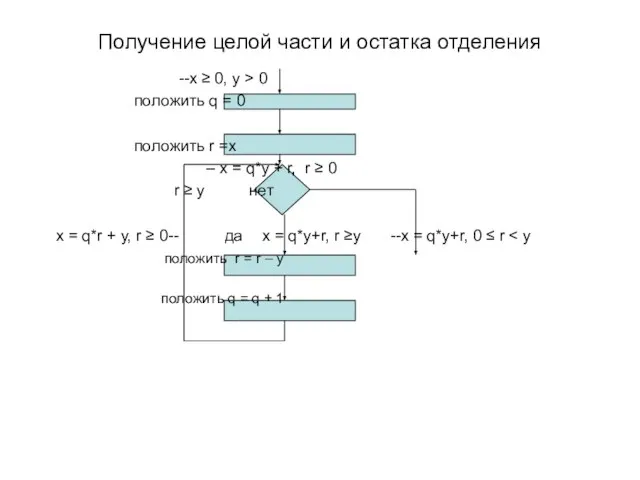
Получение целой части и остатка отделения
--x ≥ 0, y > 0
положить q = 0
положить r =x
-- x = q*y + r, r ≥ 0
r ≥ y нет
x = q*r + y, r ≥ 0-- да x = q*y+r, r ≥y --x = q*y+r, 0 ≤ r < y
положить r = r – y
положить q = q + 1

Статическая и динамическая структура программы
Каждый алгоритм имеет статическую и динамическую структуру.
Статическая структура представляется текстом программы или его
структурной схемой, описывающими действия и проверки, которые
должны быть выполнены для решения конкретной задачи.
Статическая структура, текст не зависит от исходных данных.
Динамическая структура отражает процесс вычислений и
представляет собой последовательность состояний вычислений.
ДС зависит, определяется набором исходных данных, так как от
них зависит последовательность вычислений и переходов в
программе. Текущее состояние вычислений включает в себя
значения всех программных переменных в данный момент
времени и зависит от входных данных и от предыдущих состояний
вычислений.

Спецификация программы и правила вывода
Любой оператор или изменяет состояние вычислений… или анализирует и принимает решение…
Любой язык программирования включает в себя некоторое количество простых операторов и методы объединения, композиции их в составные, структурные.
Задача: описать соотношения и правила вывода, которые позволят определить эффект воздействия простого оператора на состояние вычислений и выделить свойства составного оператора из свойств входящих в него простых операторов.
На структурной схеме нахождения div и mod определены состояния вычислений с помощью соотношений, которые должны выполняться для входных и промежуточных величин.
Фундаментальным свойством всех способов композиции является возможность объединения в одну сложную структурную схему с одним входом и одним выходом произвольного количества любых структурных схем.

Спецификация программы и правила вывода
- P
Спецификация программы: S
{ P} S { Q } (1) -Q
Если соотношение P – истинно перед выполнением S, то после завершения выполнения S, будет истинно выражение Q. …
Если S - это программа, корректность которой мы должны установить, то необходимо доказать нотацию (1), где P – соотношение, которому должны удовлетворять входные данные, а Q – выходные.
Для задачи поиска div и mod:
{(x ≥ 0) ^ (y > 0)} S {(x = q * y + r) ^ (0 ≤ r < y)}
Соотношение (1) определяет частичную корректность программы, так как S может не завершаться, точка выхода может не достигаться. Завершаемость S необходимо доказать, тогда будет доказана полная корректность.

Спецификация программы и правила вывода
Проектирование должно начинаться с определения спецификации {P} S {Q}, которой должна удовлетворять проектируемая программа, при каких условиях она должна работать (предусловие P) и какие результаты должны быть получены, каким условиям должны удовлетворять выходные данные (постусловие Q).
Процесс проектирования сверху вниз определяет спецификации {Pi} Si {Qi} для компонент программы Si
Проектирование программы осуществляется одновременно с доказательством корректности этих спецификаций.

Представим блок-схему этого алгоритма как композицию…..
x>=0, y>0 x>=0, y> 0
s1 q = 0;
r>=0 s1 r = x;
s3
x=q*y+r, 0<= r
=0

x = q*y + r, r >=y
S3 r = r – y; s2 q = q + 1;
x = q * y +r , r >=O

Правила вывода
Правила вывода – это схемы рассуждений, позволяющие доказывать свойства программ. Общий вид:
H1,H2,…Hn
H
Если над чертой истинные выражения, то и под чертой выражение будет истинным.
Первое правило консеквенции:
{P} S {R}, R Q
{P} S {Q}
Например:
{(x > 0) ^ (y > 0)} S {(z + u * y = x * y) ^ (u = 0)},
(z + u * y = x * y) ^ (u = 0) (z = x * y)
{(x > 0) ^ (y > 0)} S {(z = x * y)}

Второе правило консеквенции:
P R, {R} S {Q}
{P} S {Q}
Например:
((x = y * q + r) ^ (r > y)) (x = y * (1 + q) + (r – y),
{x = y * (1 + q) + (r – y)} r = r – y { x = y * (1 + q) + r}
{(x = y * q + r) ^ (r > y)} r = r – y { x = y * (1 + q) + r}

Правила вывода для операторов языка программирования

Правила вывода для структурных операторов
Простейшей формой структурирования является создание составных операторов с помощью последовательной композиции действий S1, S2,… Sn.
В С++ составной оператор - {S1; S2;… Sn;}

Правила вывода для составного и условных операторов

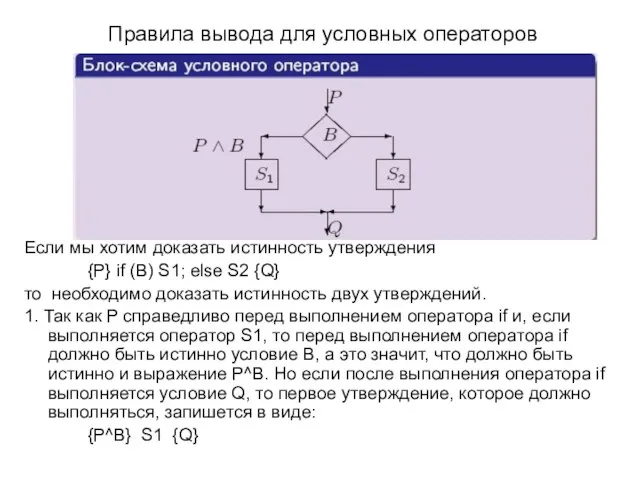
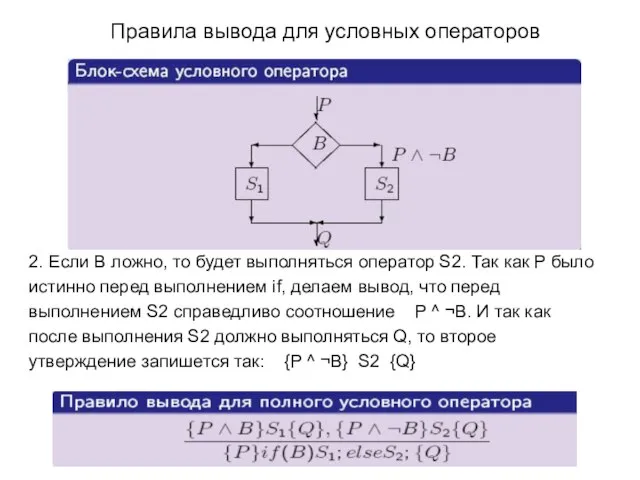
Правила вывода для условных операторов
Если мы хотим доказать истинность утверждения
{P} if (B) S1; else S2 {Q}
то необходимо доказать истинность двух утверждений.
1. Так как P справедливо перед выполнением оператора if и, если выполняется оператор S1, то перед выполнением оператора if должно быть истинно условие B, а это значит, что должно быть истинно и выражение P^B. Но если после выполнения оператора if выполняется условие Q, то первое утверждение, которое должно выполняться, запишется в виде:
{P^B} S1 {Q}

Правила вывода для условных операторов
2. Если B ложно, то будет выполняться оператор S2. Так как P было
истинно перед выполнением if, делаем вывод, что перед
выполнением S2 справедливо соотношение P ^ ¬B. И так как
после выполнения S2 должно выполняться Q, то второе
утверждение запишется так: {P ^ ¬B} S2 {Q}

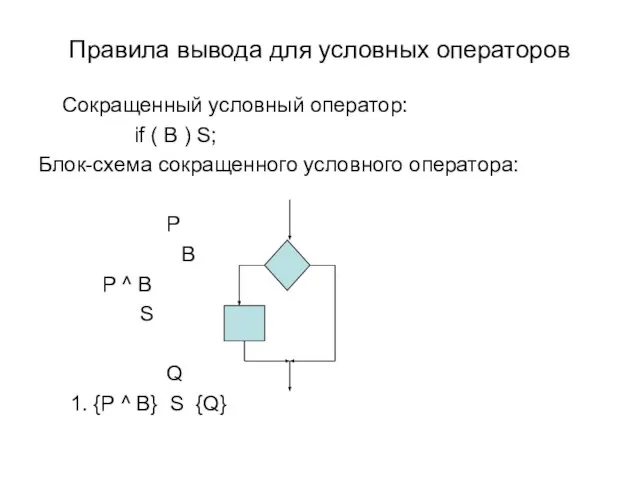
Правила вывода для условных операторов
Сокращенный условный оператор:
if ( B ) S;
Блок-схема сокращенного условного оператора:
P
B
P ^ B
S
Q
1. {P ^ B} S {Q}

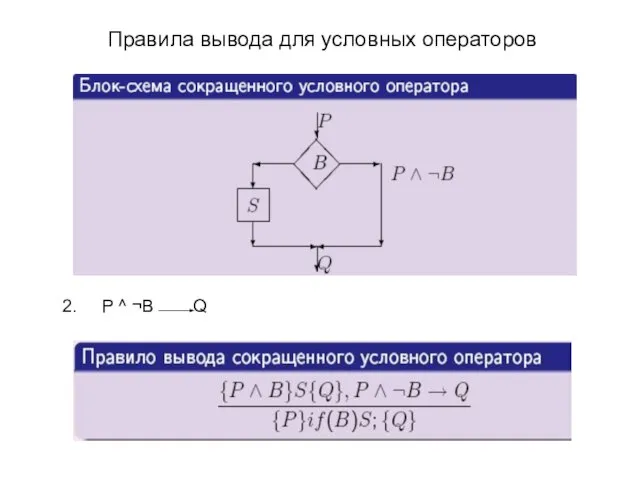
Правила вывода для условных операторов
2. P ^ ¬B Q

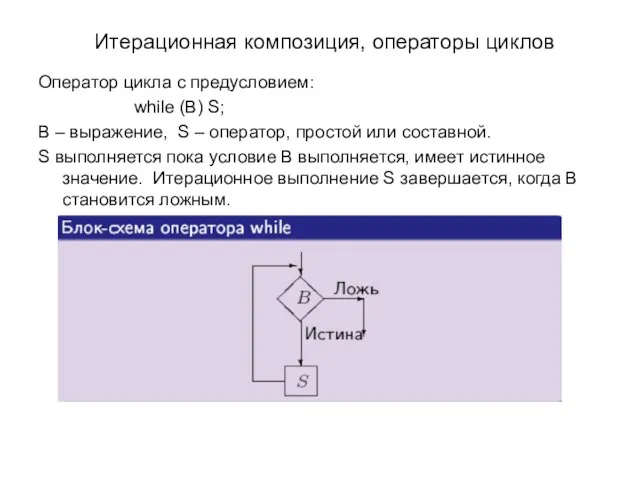
Итерационная композиция, операторы циклов
Оператор цикла с предусловием:
while (B) S;
B – выражение, S – оператор, простой или составной.
S выполняется пока условие B выполняется, имеет истинное значение. Итерационное выполнение S завершается, когда B становится ложным.

Итерационная композиция, операторы циклов
Если P справедливо, когда впервые входим в цикл, то P^B будет справедливо,
если мы достигнем точки C. Если же придем в точку D, т.е. цикл завершится
нормально, то должно выполняться условие P^ ¬ B. Но после выполнения
оператора S, мы снова попадем в точку А и снова должно выполняться
условие P. Т.е. в точке A условие P, а в точке С условие P^B , будут
выполняться столько раз, сколько раз выполняется тело цикла.
{ P ^ B } S { P }
{ P } while (B) S; { P ^ ¬ B }
Говорят, что это правило устанавливает свойство инвариантности утверждения P, поэтому P называют инвариантом цикла.

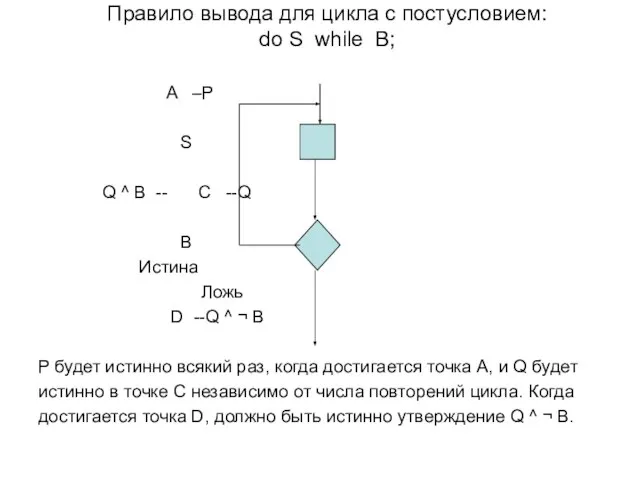
Правило вывода для цикла с постусловием:
do S while B;
A –P
S
Q ^ B -- C --Q
B
Истина
Ложь
D --Q ^ ¬ B
P будет истинно всякий раз, когда достигается точка A, и Q будет
истинно в точке С независимо от числа повторений цикла. Когда
достигается точка D, должно быть истинно утверждение Q ^ ¬ B.

Доказательство правильности алгоритма поиска div и mod
Представим блок-схему этого алгоритма с учетом его декомпозиции
-- x>=0, y>0 --x>=0, y> 0
s1 q = 0;
-- x=q*y+r, r>=0 s1 r = x;
s3
-- x=q*y+r, 0<= r
=0
Пример.
Правило вывода для цикла с постусловием:
{ P } S { Q }, Q ^ B P
{ p } do S while (B); { Q ^ ¬ B }

Доказательство правильности алгоритма поиска div и mod
x=q*y + r, r>=y
S3 r = r – y;
s2 q = q + 1;
x = q * y +r , r>=O

Фрагмент программы

Рассмотрим вначале цикл, представленный блоком s3
B - это (r >= y) , отрицание B – это ( r < y )
Переписав выходное соотношение с использованием этих выражений, получим:
Т.е. необходимо доказать, корректность цикла

Для этого необходимо доказать, что справедливо соотношение над чертой, в нашем случае
где s2 – составной оператор, отраженный блок-схемой. Докажем
это соотношение. Для этого используем утверждение, которое
следует из того, что если из r вычесть y, то к q необх. прибавить 1.
Используем дважды правило вывода для оператора присваивания

Теперь используем правило составного оператора и 2-е правило консеквенции
получим

Использовав эти три соотношения и правило консеквенции, получим соотношение для s1.
{(x>=0) (y>0)} s1 {(x = q*y + r) (r>=0)}
Это и есть выражение над чертой в нашем случае -
{P^B} S2 {P}, т. обр. правило вывода для цикла s3 доказано.

Осталось доказать спецификацию для составного оператора
{ s1;s3}

Мы доказали частичную корректность алгоритма, так как при доказательстве не использовалось условие y>0. Это условие используется для доказательства завершаемости алгоритма.

Доказательство завершаемости алгоритмов
Деление целых неотрицательных чисел.
-----------------------------------------
{x >= 0, y > 0}
q = 0; r = x;
{r + y > 0}
while (r >= y)
{r = r – y; q = q + 1
{r + y > 0}
}
Инвариантом цикла является выражение r + y > 0 и это
выражение остается большим нуля и на каждом шаге цикла
уменьшается за счет оператора r = r – y. Следовательно, цикл
может повторяться только конечное число раз, исходя из условий
x > 0 и y > 0

Доказательство завершаемости алгоритмов
Используя условие y > 0, доказали завершаемость алгоритма,
Сочетание доказательства частичной корректности алгоритма,
выполненное с использованием условия x > 0, с доказательством
завершаемости алгоритма дает полную корректность программы.
Если не удается найти выражение, которое будет инвариантом цикла, это еще не значит, что алгоритм не обладает завершенностью, необходимо доказать, что инвариантом является не только предусловие
{ P } но и условие {P ^ B} для цикла c предусловием и условие {Q ^ B} для цикла с постусловием.
.

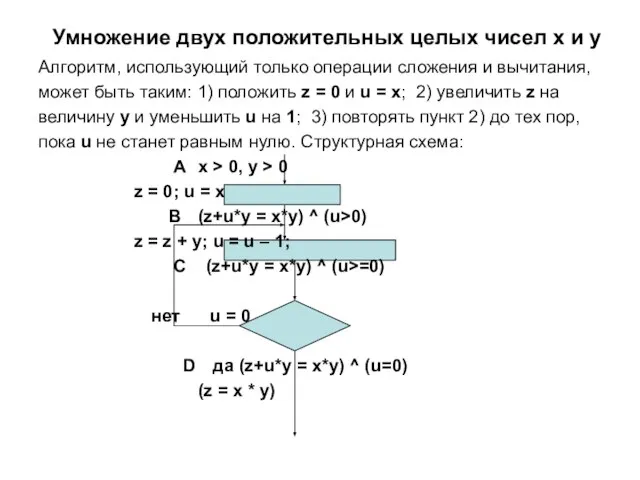
Умножение двух положительных целых чисел x и y
Алгоритм, использующий только операции сложения и вычитания,
может быть таким: 1) положить z = 0 и u = x; 2) увеличить z на
величину y и уменьшить u на 1; 3) повторять пункт 2) до тех пор,
пока u не станет равным нулю. Структурная схема:
A x > 0, y > 0
z = 0; u = x
B (z+u*y = x*y) ^ (u>0)
z = z + y; u = u – 1;
C (z+u*y = x*y) ^ (u>=0)
нет u = 0
D да (z+u*y = x*y) ^ (u=0)
(z = x * y)

Соотношения в точках B,C и D отражают суть алгоритма:
z используется для накопления суммы, u определяет
сколько еще раз нужно вычислить сумму, чтобы
получить произведение x*y , т.е. как раз справедливо
соотношение z + u * y = x * y. И это соотношение
является инвариантом цикла, что отражает блок-схема.
Перед очередным умножением в точке B u > 0, а в
точке C может быть u >=0. Реализация алгоритма:
{(x>0) ^ (y>0)}
{ z = 0; u = x;
do
z = z + y; u = u - 1;
while (u <> 0);
};
{ (z = x * y)}

Применяем правила вывода для доказательства правильности алгоритма:
Из исходных условий можно записать:
((x>0) ^ (y>0)) ((x*y = x*y) ^ (x>0)
Применив правило вывода для составного оператора, расположенного между точками A и B, получим:
{(x*y = x*y) ^ (x>0)} {z = 0; u = x;} {(z+u*y = x*y) ^ (u > 0)}
Использовав второе правило консеквенции, получим:
{(x>0) ^ (y>0)} {(z = 0); (u = x)} {(z+u*y = x*y) ^ (u > 0)}
Теперь используем правило вывода для составного оператора, заключенного между точками B и C:
(*) {(z+u*y = x*y) ^ (u>0)} {z = z+y; u = u - 1} {(z+u*y = x*y) ^ (u≥0)}
Здесь постусловие соответствует точке С, и если по схеме попадем на ветвь, когда u ≠ 0, то верно будет соотношение:
(**) ((z+u*y = x*y) ^ (u ≥ 0) ^ ¬(u = 0)) ((z+u*y = x*y) ^ (u > 0))

Используем правило вывода для оператора цикла с постусловием
{P} S {Q}, Q ^ B P
{P} do s; while (B); {Q ^ ¬ B}
Если S – это операторы, стоящие между точками B и C,
а P и Q – это предусловие и постусловие в выражении (*),
тогда (*) и (**) – это правильные утверждения, стоящие
над чертой, а это значит, что справедливо и
утверждение, записанное под чертой, т.е. корректна:
{(z+u*y = x*y) ^ (u > 0))}
do
z = z+y; u = u – 1;
while (u = 0);
{(z + u * y = x * y) ^ (u≥0) ^ (u = 0)}

Из постусловия этого утверждения следует
((z + u * y = x * y) ^ (u≥0) ^ (u = 0)) z = x * y
И, наконец, используем правило вывода для составного оператора S1, S2, получим:
{(x > 0) ^ (y > 0)} S1; S2; {z = x * y}
Доказали частичную корректность алгоритма суммирования целых неотрицательных чисел.