ДУ Информатика 8.12

Задание
Запишите тему в тетради: «Умножение и деление чисел в различных системах счисления»
Прочитайте презентацию
Запишите в тетради общее правило умножения чисел и 2-3 примера.
Самостоятельно выполните 2 примера на умножение из Реши сами
Запишите в тетради общее правило деления чисел и 2-3 примера.
Самостоятельно выполните 2 примера на деление из Реши сами
Домашнее задание: прочитать § 12 (3, 4), письменно стр. 128 № 1 (4, 5). Сфотографируйте и отправьте мне 8.12.2021 (среда)

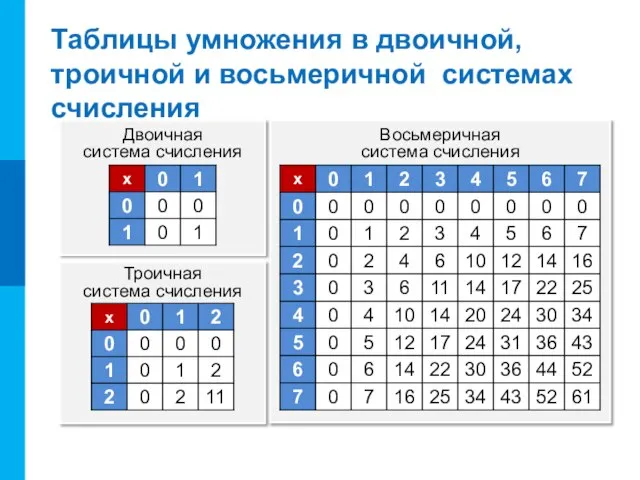
Таблицы умножения в двоичной, троичной и восьмеричной системах счисления
Двоичная
система счисления
Восьмеричная
система счисления
Троичная система счисления

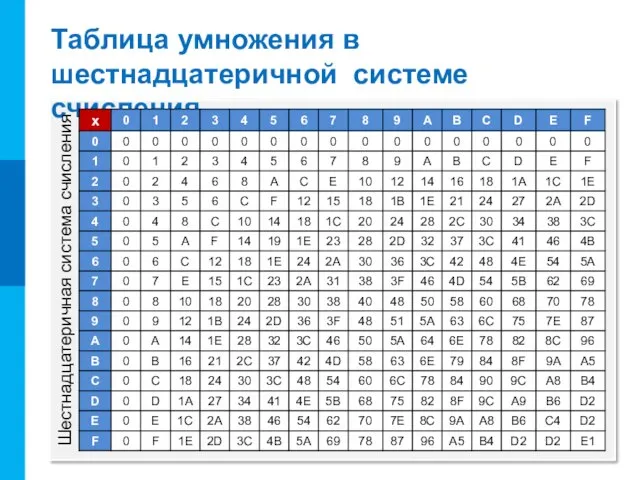
Таблица умножения в шестнадцатеричной системе счисления
Шестнадцатеричная система счисления

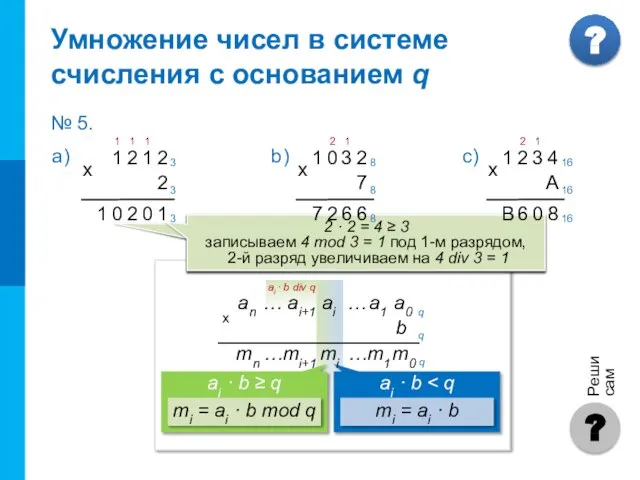
ai · b div q
Чтобы в системе счисления q получить произведение M многозначного числа A и однозначного числа b, надо вычислить произведения b и цифр числа A по разрядам i :
Умножение многозначного числа на однозначное в системе счисления q
если ai · b < q, то mi = ai · b,
старший (i + 1)-й разряд не изменяется
если ai · b ≥ q, то mi = ai · b mod q,
старший (i + 1)-й разряд увеличивается на ai · b div q

1 · 2 + 1 = 3 ≥ 3
записываем 3 mod 3 = 0 под 2-м разрядом,
3-й разряд увеличиваем на 3 div 3 = 1
2 · 2 + 1 = 3 ≥ 3
записываем 5 mod 3 = 2 под 3-м разрядом,
4-й разряд увеличиваем на 5 div 3 = 1
2 · 1 + 1 = 3 ≥ 3
записываем 3 mod 3 = 0 под 4-м разрядом
и в 5-й разряд записываем 3 div 3 = 1
2 · 2 = 4 ≥ 3
записываем 4 mod 3 = 1 под 1-м разрядом,
2-й разряд увеличиваем на 4 div 3 = 1
Умножение чисел в системе
счисления с основанием q
3
а)
7
2
6
6
2
1
8
b)
?
Реши сам
№ 5.
1
0
2
0
1
1
1
1
В
6
0
8
2
1
16
с)

Решите самостоятельно
ОТВЕТ
№ 6.

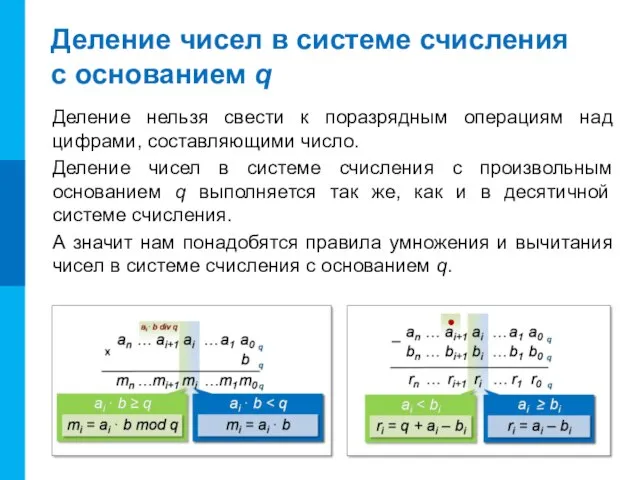
Деление нельзя свести к поразрядным операциям над цифрами, составляющими число.
Деление чисел в системе счисления с произвольным основанием q выполняется так же, как и в десятичной системе счисления.
А значит нам понадобятся правила умножения и вычитания чисел в системе счисления с основанием q.
Деление чисел в системе счисления
с основанием q