Содержание
- 2. "Мысль выражать все числа десятью знаками, придавая им кроме значения по форме еще значение по месту,
- 3. Наиболее известные нумерации мира Древнеегипетская нумерация Древнегреческая нумерация Вавилонская нумерация Нумерация индейцев Майя Старо-Китайская нумерация Славянская
- 4. Египетская нумерация 1. Как и большинство людей для счета небольшого количества предметов Египтяне использовали палочки. Если
- 5. 10. Такими путами египтяне связывали коров Если нужно изобразить несколько десятков, то иероглиф повторяли нужное количество
- 6. Древняя греческая нумерация 1, 2, 3, 4 6, 7, 8, 9 10
- 8. Вавилонская нумерация 1 10 0
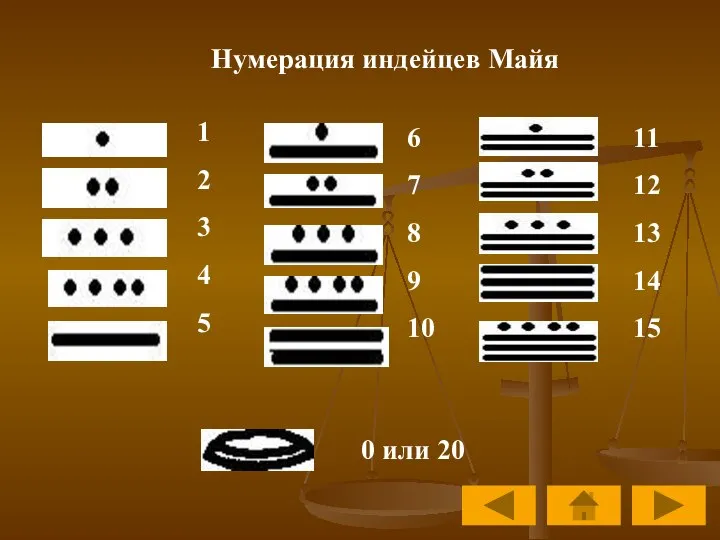
- 9. Нумерация индейцев Майя 1 2 3 4 5 6 7 8 9 10 11 12 13
- 10. Китайская нумерация ° 1 2 3 4 5 6 7 8 9 0 10 100 1000
- 11. Славянская кириллическая нумерация
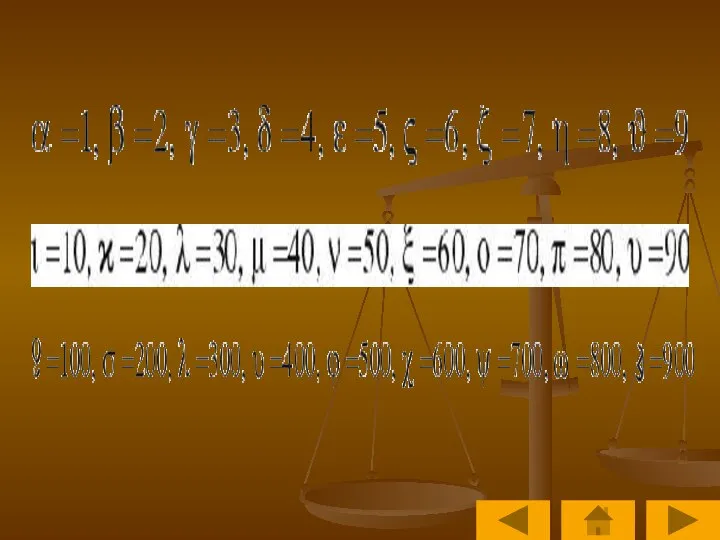
- 12. Славянская глаголическая нумерация 1 2 3 4 5 6 7 8 9 10 20 30 40
- 13. Латинская (Римская) нумерация I 1 V 5 X 10 L 50 C 100 D 500 M
- 14. Арабская системы счисления Впервые такая система, вернее ее зачатки появилась в Древнем Вавилоне, почти в то
- 15. Позиционные системы счисления
- 16. Правило. Для перевода целого числа N в систему счисления с основанием q необходимо разделить N на
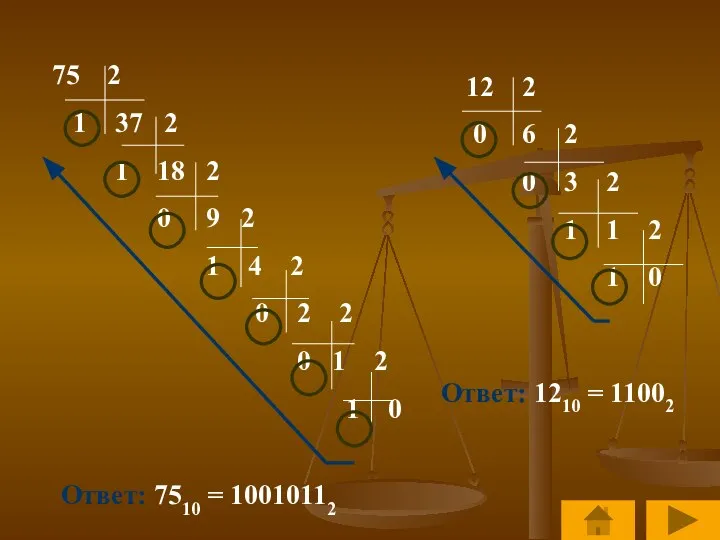
- 17. Примеры: Переведем числа 75 и 12 из десятичной системы счисления в двоичную.
- 18. 2 1 37 2 1 18 2 0 9 2 1 4 2 0 2 2
- 19. Задание. Переведите десятичные числа в двоичную. 1 вариант - 25 и 42 2 вариант - 35
- 20. Ответы: 2510 = 110012 3510 = 1000112 4210 =1010102 3010 = 111102
- 21. Правило. Для перевода правильной десятичной дроби N в систему счисления с основанием q необходимо умножить N
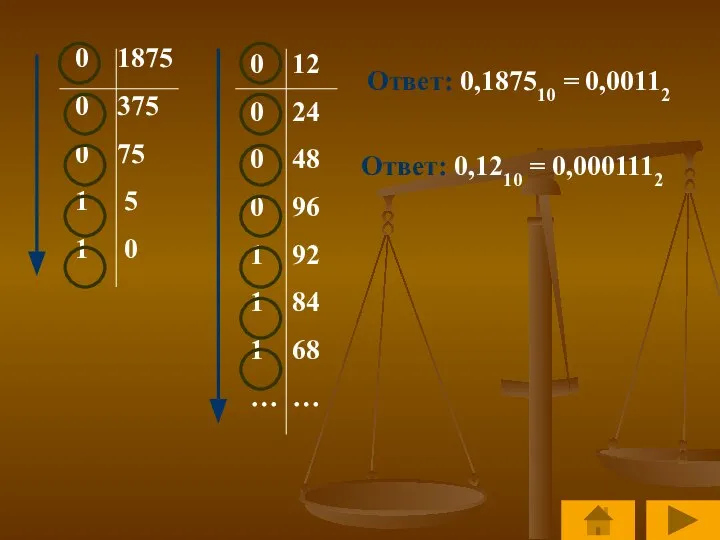
- 22. Примеры: Переведем число 0,1875 и 0,12 (с точностью до 6 знаков) из десятичной системы счисления в
- 23. 0 1875 0 375 0 75 1 5 1 0 Ответ: 0,187510 = 0,00112 0 12
- 24. Задание. Переведите десятичные дробные числа в двоичную. 1 вариант - 0,25 и 0,3 (с точностью 4
- 25. Ответы: 0,2510 = 0,012 0,7510 = 0,112 0,310 = 0,01002 0,410 = 0,01102
- 26. Правило. Для перевода числа х (хq = апап-1…а0,а-1а-2…а-т) из системы счисления с основанием q (q=2, 8
- 27. Примеры: Переведем число 111001,12 в десятичную систему счисления. 111001,12 = 1. 25 + 1.24 + 1.23
- 28. Задание: Переведите числа в десятичную систему счисления. 1 вариант - 1 111, 012 2 вариант -
- 29. Ответы: 1 111, 012 = 15, 2510 10 000, 0012 = 16, 12510
- 30. Домашнее задание. Переведите числа из десятичной системы счисления в двоичную: 100,45 99 0,8125 2. Переведите число
- 31. Дополнительное задание. Переведите в двоичную. 200410 и 300410 Ответы: 200410 = 11 111 010 1002 300410
- 33. Скачать презентацию


























 Подготовили Батуева Л.Н.-учитель математики МБОУ СОШ №11 г.Чайковский , Маркова Е.В- учитель информатики МБОУ СОШ №11 г.Чайковск
Подготовили Батуева Л.Н.-учитель математики МБОУ СОШ №11 г.Чайковский , Маркова Е.В- учитель информатики МБОУ СОШ №11 г.Чайковск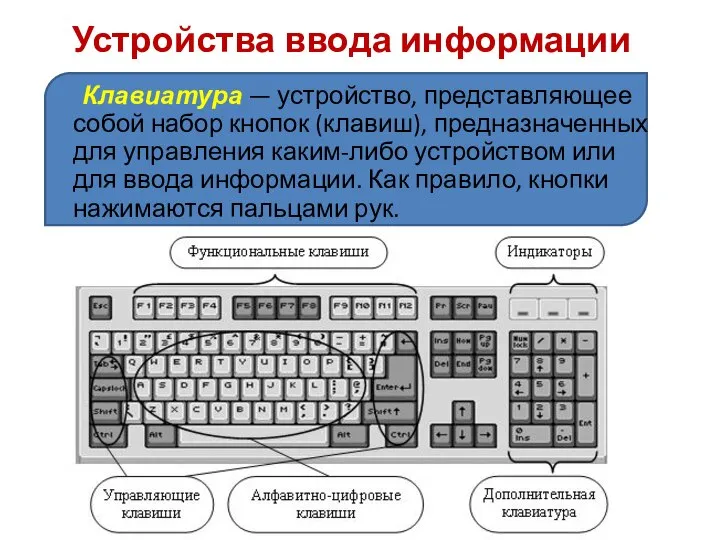 Устройства ввода информации
Устройства ввода информации Обои для презентации
Обои для презентации Readsee/Ридси. Читай и вдохновляйся
Readsee/Ридси. Читай и вдохновляйся Исследование подходов для аутентификации пользователей беспроводной сети с применением различных LDAP решений
Исследование подходов для аутентификации пользователей беспроводной сети с применением различных LDAP решений Математические основы информатики. Общие сведения о системах счисления
Математические основы информатики. Общие сведения о системах счисления 0821dd87747943779db6c0c7e5802e37
0821dd87747943779db6c0c7e5802e37 Безопасность детей в Интернете
Безопасность детей в Интернете Digital Paper. Цифровая бумага. Новый цифровой носитель информации
Digital Paper. Цифровая бумага. Новый цифровой носитель информации Технические средства обучения
Технические средства обучения Логические основы ЭВМ
Логические основы ЭВМ Визуальная среда математического моделирования MathCAD
Визуальная среда математического моделирования MathCAD Компьютерные технологии в спорте
Компьютерные технологии в спорте Системы счисления
Системы счисления Цветовая модель RGB
Цветовая модель RGB Как не убить канал YouTube рекламой и почему она эффективна
Как не убить канал YouTube рекламой и почему она эффективна Моделирование и формализация
Моделирование и формализация Моя жизнь на Amazing RP
Моя жизнь на Amazing RP Сервісні програми ОС
Сервісні програми ОС Надстройка Пакет анализа в Excel
Надстройка Пакет анализа в Excel Представление графов. Топологическая сортировка
Представление графов. Топологическая сортировка Объект и его свойства
Объект и его свойства Проектирование. Диаграммы
Проектирование. Диаграммы Ввод и редактирование данных в редакторе Excel
Ввод и редактирование данных в редакторе Excel Информация и её свойства. Информация и информационные процессы
Информация и её свойства. Информация и информационные процессы Операторы условия, цикла, функции
Операторы условия, цикла, функции Обработка символьной информации в языке Pascal
Обработка символьной информации в языке Pascal Паскаль. Циклические вычисления
Паскаль. Циклические вычисления