Слайд 2ОСНОВНЫЕ ПОНЯТИЯ АНАЛИЗА
Программное обеспечение SW использует метод конечных элементов (МКЭ). МКЭ –

это численный метод анализа технических конструкций. МКЭ принят в качестве стандартного метода анализа благодаря его универсальности и пригодности для работы на компьютерах. МКЭ делит модель на много малых частей простых форм, называемых элементами, эффективно заменяющими сложную задачу несколькими простыми, которые необходимо решить совместно.
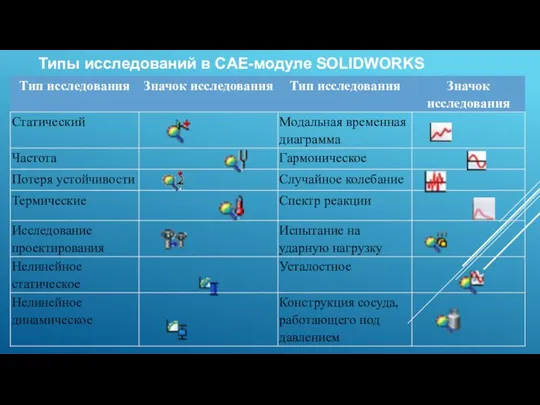
Слайд 3Типы исследований в CAE-модуле SOLIDWORKS
Слайд 4ШАГИ АНАЛИЗА
Модель обычно подвергается воздействию различных технических сред и условий эксплуатации во

время ее срока службы. Очень важно учитывать все возможные сценарии нагрузок и граничные условия и попытаться использовать материал другими свойствами в анализе модели.
Исследование моделирования определяется следующими факторами:
1. Размеры модели
2. Тип исследования и связанные параметры, чтобы определить назначение анализа
3. Свойства материала
4. Нагрузки и граничные условия
5. Задание сетки:
• Программа автоматически создает сетку оболочки для поверхностей и листового металла с равномерной толщиной
• Программа автоматически создает сетку элементы конструкции с балочными элементами
• Программа автоматически создает комбинированную сетку, когда в модели присутствуют разные геометрические тела (твердые тела, оболочки, элементы конструкции и т.п.).
Слайд 5МАТЕРИАЛЫ
Модель материала описывает поведение материала и определяет требуемые свойства материала.
Линейные

изотропные и ортотропные модели материала доступны для всех конструкционных и термических исследований.
Другие модели материалов доступны для нелинейных исследований напряжения.
Пластичная модель по Мизесу может подвергаться исследованиям на ударную нагрузку.
Свойства материала могут быть заданы в качестве функции температуры.
Слайд 6КРЕПЛЕНИЯ И НАГРУЗКИ
Крепления и нагрузки определяют условия среды модели.
Программное обеспечение

предоставляет контекстные параметры для определения ограничений. Например, если все выбранные поверхности являются цилиндрическими или выбрана координатная ось, программа ожидает, что вы определите радиальные, окружные и осевые ограничения.
Для нелинейных и переходных термических исследований крепления и нагрузки определяются в качестве функции времени.
Слайд 7ЛИНЕЙНЫЙ СТАТИЧЕСКИЙ АНАЛИЗ
Тело, когда к нему применяются нагрузки, деформируется и воздействие нагрузок

передается через все тело. Внешние нагрузки включают в себя внутренние силы и реакции, которые компенсируют воздействия и возвращают тело в состояние равновесия. Линейный статический анализ рассчитывает силы перемещений, напряжения, нагрузки и реакции при воздействии приложенных нагрузок.
В линейном статическом анализе используются следующие допущения:
Допущение статики Все нагрузки прилагаются медленно и постепенно, пока не достигнут своих полных величин. По достижению своих полных величин нагрузки остаются постоянными (неизменными по времени). Такое допущение позволяет пренебречь внутренними и демпфирующими силами ввиду пренебрежимо малых ускорений и скоростей.
• Для расчета реакции тел конструкции, вращающихся с постоянной скоростью или перемещающихся при постоянных ускорениях, можно воспользоваться статическим анализом ввиду того, что генерируемые нагрузки не меняются во времени.
Допущение линейности. Взаимоотношения между нагрузками и вызванными реакциями предполагаются линейными. Если, например, увеличить вдвое величину нагрузок, реакция модели (перемещения, нагрузки и напряжения) также увеличится вдвое. Можно принимать допущение линейности, если:
• все материалы в модели подчиняются закону Гука, в соответствии с которым напряжение прямо пропорционально деформации.
• вызванные перемещения достаточно малы, чтобы можно было пренебречь изменениями в жесткости, вызванными нагружением.
• Граничные условия не изменяются во время приложения нагрузок. Нагрузки должны быть постоянными по величине, направлению и распределению. Они не должны изменяться во время деформирования модели.
Слайд 8АНАЛИЗ ТЕРМИЧЕСКИХ НАПРЯЖЕНИЙ
Изменения температуры могут повлечь за собой значительные изменения формы, деформации
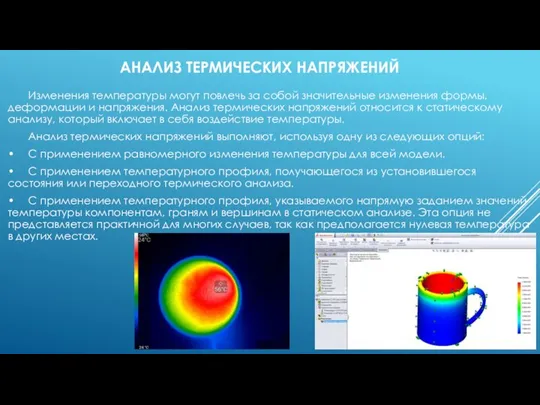
и напряжения. Анализ термических напряжений относится к статическому анализу, который включает в себя воздействие температуры.
Анализ термических напряжений выполняют, используя одну из следующих опций:
• С применением равномерного изменения температуры для всей модели.
• С применением температурного профиля, получающегося из установившегося состояния или переходного термического анализа.
• С применением температурного профиля, указываемого напрямую заданием значений температуры компонентам, граням и вершинам в статическом анализе. Эта опция не представляется практичной для многих случаев, так как предполагается нулевая температура в других местах.
Слайд 9ЧАСТОТНЫЙ АНАЛИЗ
Каждая конструкция имеет тенденцию вибрировать на
определенных частотах, называемых собственными или

резонансными частотами.
Каждая частота собственных колебаний ассоциируется с
определенной формой, называемой формой колебаний,
которую модель стремится принимать при вибрировании на этой частоте.
Когда конструкция возбуждена динамической нагрузкой на частоте, которая совпадает с одной из ее собственных частот, конструкция подвергается большим перемещениям и напряжениям. Настоящее явление называется резонансом.
Для недемпфированных систем резонанс вызывает теоретически бесконечное движение. Демпфирование, однако, ограничивает реакцию конструкции, вызванную резонансными нагрузками.
Частотные исследования могут помочь избежать резонанса и при проектировании систем виброизоляции. Они также формируют базу для оценки реакции линейных динамических систем, в которых реакция системы на динамическую среду принимается равной сумме вкладов мод, учитываемых в анализе.
Конечноэлементная модель имеет конечное количество собственных частот, которое равно числу степеней свободы, учитываемых в модели. Для большинства задач необходимы только первые несколько мод.
Собственные частоты и соответствующие формы колебаний зависят от формы, свойств материала и условий опирания. Вычисление собственных частот и форм колебаний называется модальным анализом, частотным анализом и анализом собственных колебаний.
Слайд 10ДИНАМИЧЕСКИЙ АНАЛИЗ
Статические исследования предполагают, что нагрузки являются постоянными или прикладываются медленно до

тех пор, пока они не достигают полных значений. Вследствие настоящего допущения скорость и ускорение каждой частицы модели принимаются нулевыми. В результате, статические исследования пренебрегают инерционными силами и силами демпфирования.
Во многих практических случаях нагрузки прикладываются быстро или изменяются со временем или по частоте. Для таких случаев применяют динамическое исследование. В общем, если частота нагрузки больше чем 1/3 самой низкой (основной) частоты, следует использовать динамическое исследование.
Динамический анализ позволяет рассчитывать меняющиеся по времени нагрузки, включающие существенные внутренние и/или демпфирующие силы, пренебречь которыми нельзя.
Слайд 11ДИНАМИЧЕСКИЙ АНАЛИЗ (2)
Динамическая нагрузка может вызвать напряжения, составляющие до 1/(2x) величины напряжений,

генерируемых статическими нагрузками с такими же значениями, где x – коэффициент вязкостного демпфирования.
Для слабо демпфированных конструкций при демпфировании 5% динамические напряжения будут в 10 раз больше, чем статические напряжения. Сценарий наихудшей ситуации проявляется при явлении резонанса.
Динамические нагрузки включают в себя осциллирующие нагрузки, удары, соударения и случайные нагрузки.
Цели динамического анализа включают:
• Проектирование структурных и механических систем для работы без разрушения в динамических средах.
• Модификацию характеристик системы (то есть, формы, механизмов демпфирования, свойств материала, и т. п.), чтобы уменьшить влияние вибрации.
Слайд 12ДИНАМИЧЕСКИЙ АНАЛИЗ (3) УРАВНЕНИЯ ДВИЖЕНИЯ
Системы с одной степенью свободы (SDOF)
Рассмотрим простую упругую

систему с массами. Масса (m) подвергнута воздействию силы F(t) в направлении u в качестве функции времени. Масса может перемещаться только в направлении u и, следовательно, является системой с одной степенью свободы (SDOF). Движению сопротивляется пружина жесткостью (к).
Записывая второй закон Ньютона (сила равна массе, умноженной на ускорение) для этой системы во время (t), получаем:
F(t)-ku(t) = mu(t), или
mu(t) + ku(t) = F(t), где
u(t) – ускорение массы во время (t) и оно равно второй производной u относительно времени.
k = жесткость пружины
Слайд 13ДИНАМИЧЕСКИЙ АНАЛИЗ (4) УРАВНЕНИЯ ДВИЖЕНИЯ
Системы с одной степенью свободы (SDOF)
При вязкостном демпфировании

предполагаем, что демпфирующая сила пропорциональна скорости. С учетом демпфирования вышеприведенное уравнение становится: mu(t) + cu(t) + ku(t) = F(t), где:
u(t) – скорость массы во время (t) и оно равно первой производной u относительно времени.
Слайд 14ДИНАМИЧЕСКИЙ АНАЛИЗ (5) УРАВНЕНИЯ ДВИЖЕНИЯ
Системы со многими степенями свободы (MDOF)
Для систем со

многими степенями свободы (MDOF) m, c и k становятся матрицами, а не одиночными значениями и уравнения движения выражены как:
где:
[M]: матрица масс
[K] : матрица жесткости
[C] : матрица демпфирования
{u(t)}: вектор перемещения во время t (составляющие перемещения каждого узла)
: вектор ускорения во время t (ускорение компонентов каждого узла)
: вектор скорости во время t (скорость компонентов каждого узла)
{f(t)}: изменяющийся во времени вектор нагрузки (сила компонентов каждого узла)
Слайд 15ГАРМОНИЧЕСКИЙ АНАЛИЗ
Используйте гармонический анализ для вычисления максимальной реакции в установившемся состоянии, вызванной

гармоническими нагрузками или возбуждениями основания.
Гармоническая нагрузка Р выражена в виде Р = A sin (ωt + φ), где: A – амплитуда, ω – частота, t – время, а φ – фазовый угол.
Примеры гармонических нагрузок различных частот w относительно времени :
Слайд 16ГАРМОНИЧЕСКИЙ АНАЛИЗ (2)
Например, электродвигатель, установленный на испытательном столе, передает гармонические нагрузки на

несущую конструкцию через болты. Можно смоделировать несущую конструкцию и определить гармоническое исследование, чтобы
оценить установившиеся максимальные
перемещения, напряжения, и т. п. для диапазона
рабочих частот электродвигателя.
Можно аппроксимировать электродвигатель
посредством распределенной массы.
После запуска исследования, можно просматривать максимальные напряжения, перемещения, ускорения и скорости, а также фазовые углы в диапазоне рабочих частот.
Слайд 17АНАЛИЗ СПЕКТРА РЕАКЦИИ
В анализе спектра реакции результаты модального анализа используются для

известного спектра для расчета смещений и напряжений в модели.
Для каждого узла реакция берется из спектра моделирования, основанного на модальной частоте и коэффициента демпфирования.
Все модальные реакции затем комбинируются для приблизительной оценки общей реакции конструкции.
Слайд 18АНАЛИЗ СПЕКТРА РЕАКЦИИ (2)
Спектр реакции создает эпюру максимальной реакции во времени

для диапазона систем с одной степенью свободы, подвергающихся определенному движению однородного основания как функции их собственных частот ω1или периода колебания T1. Каждая кривая спектра реакции соответствует определенному коэффициенту модального демпфирования ξ1.
Типичные показатели в эпюре спектра реакции:
• Максимальное смещение Sd (ω1, ξ1)
• Максимальная псевдоскорость Sv(ω1, ξ1) = ω1 *Sd
• Максимальное псевдоускорение Sa (ω1, ξ1) = ω1 *Sv = ω12 *Sd
Слайд 19АНАЛИЗ СПЕКТРА РЕАКЦИИ (3)
Спектр реакции относительного смещения для определенного соотношения затухания

ξ1.
равен максимальному абсолютному значению исторической реакции времени относительного смещения для каждого осциллятора SDOF
Слайд 20АНАЛИЗ СПЕКТРА РЕАКЦИИ (4)
Спектр реакции относительного смещения для определенного соотношения затухания
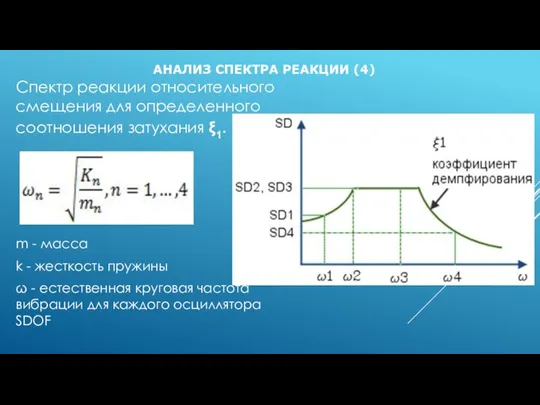
ξ1.
m - масса
k - жесткость пружины
ω - естественная круговая частота вибрации для каждого осциллятора SDOF
Слайд 21МЕХАНИЗМЫ ТЕПЛОПЕРЕДАЧИ
Проводимость
Проводимость представляет собой механизм переноса тепла, в котором термическая энергия переносится

от одной точки к другой через взаимодействие между атомами или молекулами материи.
Проводимость не включает какое-либо объемное движение материи. Газы переносят тепло прямым соударением между энергетическими молекулами и их теплопроводность ниже по сравнению с твердыми телами, так как они представляют собой разреженную среду.
Поведение энергии в жидкостях такое же, как и в газах, за исключением того, что ситуация здесь значительно сложнее, так как молекулы располагаются намного ближе друг к другу и поля сил молекулярного взаимодействия оказывают значительное влияние на энергетический обмен в процессе соударений.
Неметаллические твердые тела переносят тепло колебаниями кристаллической решетки, поэтому здесь нет места движению среды по мере распространения по ней тепла.
Металлы являются лучшими проводниками по сравнению с неметаллами при нормальных температурах, так как они обладают свободными электронами, несущими термическую энергию.
Слайд 22МЕХАНИЗМЫ ТЕПЛОПЕРЕДАЧИ (2)
Перенос тепла проводимостью подчиняется закону Фурье, который устанавливает, что скорость

проведения тепла Qпроводимостиº пропорциональна площади переноса тепла (A) и температурному градиенту (dT/dx) или: Q проводимостиº= - K A (dT/dx)
где K-теплопроводность, измеряет способность материала к проведению тепла.
Единицы измерения K – Вт/мºC или
(БТЕ/с)/дюйм.ºF.
Для планарного слоя скорость теплопроводности задается отношением:
Q проводимостиº= - K A (THº- TCº)/L
Слайд 23МЕХАНИЗМЫ ТЕПЛОПЕРЕДАЧИ (3)
Конвекция
Конвекция является режимом переноса тепла,
при котором тепло переносится между
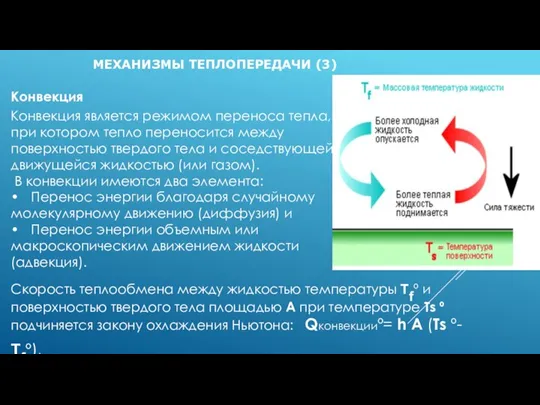
поверхностью твердого тела и соседствующей
движущейся жидкостью (или газом).
В конвекции имеются два элемента:
• Перенос энергии благодаря случайному
молекулярному движению (диффузия) и
• Перенос энергии объемным или
макроскопическим движением жидкости
(адвекция).
Скорость теплообмена между жидкостью температуры Tfº и поверхностью твердого тела площадью A при температуре Ts º подчиняется закону охлаждения Ньютона: Qконвекцииº= h A (Ts º- Tfº),
где h – коэффициент конвективной теплопередачи
Слайд 24МЕХАНИЗМЫ ТЕПЛОПЕРЕДАЧИ (4)
Излучение
Тепловое излучение представляет собой тепловую энергию, испускаемую телами в форме
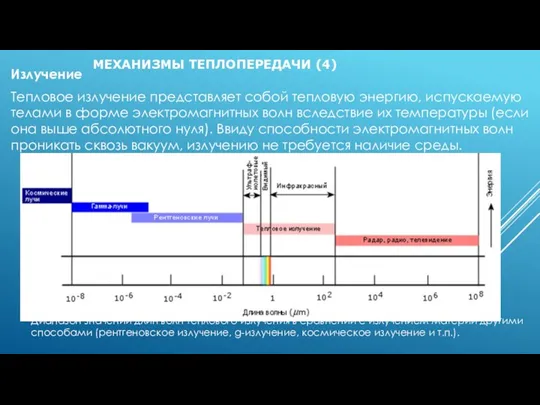
электромагнитных волн вследствие их температуры (если она выше абсолютного нуля). Ввиду способности электромагнитных волн проникать сквозь вакуум, излучению не требуется наличие среды.
Диапазон значений длин волн теплового излучения в сравнении с излучением материи другими способами (рентгеновское излучение, g-излучение, космическое излучение и т.п.).























 Лаб11
Лаб11 Симулятор установки windows 5
Симулятор установки windows 5 Виртуальный читальный зал РГБ и научный on-line ресурс ИВИС (сервис East View)
Виртуальный читальный зал РГБ и научный on-line ресурс ИВИС (сервис East View) Процессоры семейства х86. Регистры. Форматы данных. (Лекция 3)
Процессоры семейства х86. Регистры. Форматы данных. (Лекция 3) Протокол удаленного доступа Telnet
Протокол удаленного доступа Telnet Область применения контрольно-кассовой техники
Область применения контрольно-кассовой техники Одномерные массивы целых чисел. Алгоритмизация и программирование
Одномерные массивы целых чисел. Алгоритмизация и программирование Проектирование автоматизированных систем сбора данных приборов учета
Проектирование автоматизированных систем сбора данных приборов учета Контур безопасности информационных систем
Контур безопасности информационных систем Интро. Аналитик в IT
Интро. Аналитик в IT У кого что? Онлайн-игротека логопята
У кого что? Онлайн-игротека логопята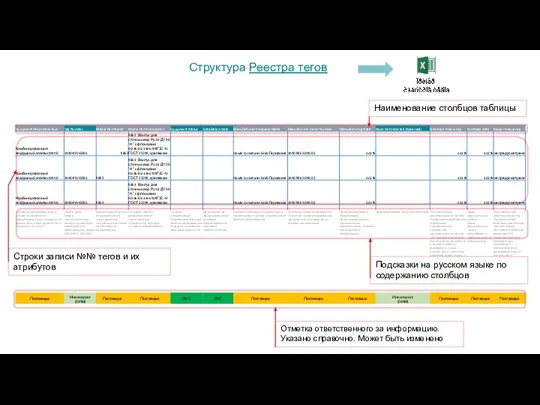 Реестры тегов
Реестры тегов Компьютерная графика
Компьютерная графика Сборки. Атрибуты
Сборки. Атрибуты Описание нормальных форм базы данных
Описание нормальных форм базы данных Autodesk inventor работа в режиме Модель. Конструкционные операции. Стратегия построения
Autodesk inventor работа в режиме Модель. Конструкционные операции. Стратегия построения Сравнение DLP систем
Сравнение DLP систем Устройство компьютера. Специальные устройства
Устройство компьютера. Специальные устройства Практичекое. Мой сайт
Практичекое. Мой сайт Reuters Group
Reuters Group 1.4.2 Кодирование чисел и текста
1.4.2 Кодирование чисел и текста Визуальное программирование. Среда программирования Scratch 3.17.2
Визуальное программирование. Среда программирования Scratch 3.17.2 Оценочная карта. Шаблон
Оценочная карта. Шаблон Тест по информатике компьютерные сети
Тест по информатике компьютерные сети Знаковые модели. Моделирование и формализация
Знаковые модели. Моделирование и формализация Автоматизация запроса персональных данных пациента, предоставление личных данных страховщику и верификация цифровых документов
Автоматизация запроса персональных данных пациента, предоставление личных данных страховщику и верификация цифровых документов Van Game's
Van Game's Отель Crowne Plaza Moscow-Tretykovskaya
Отель Crowne Plaza Moscow-Tretykovskaya