Имитационное компьютерное моделирование. Лекция 1

1. Модели и моделирование
Введем понятия «модель», «моделирование». Слово «модель» имеет франко-итальянский корни
и означает «образец». В простом варианте «модель» можно определить как копию некоторого объекта,
увеличенную или уменьшенную. Она предназначена для того, чтобы точнее изучить, проанализировать,
предвидеть то, что человек собирается создать, изготовить, построить или передать.
Моде́ль — некоторый материальный или мысленно представляемый объект или явление,
являющийся упрощѐнной версией моделируемого объекта или явления (прототипа) и в
достаточной степени повторяющий свойства, существенные для целей конкретного
моделирования (опуская несущественные свойства, в которых он может отличаться от
прототипа).
Модели бывают материальными (вещественными) или физическими и абстрактные. К
физическим моделям относятся уменьшенные макеты зданий, башень, мостов, самолетов и т.д., к
увеличенным копиям – строения атома, молекул алмаза. К абстрактным моделям относятся рисунки,
схемы, карты, а также математические, компьютерные (имитационные) и эвристические модели. Они не
являются копией оригинала, а носят описательный характер. К экономическим системам применимы
математические и имитационные модели.
Под математической моделью принято понимать совокупность соотношений – уравнений,
неравенств, логических условий, операторов и т.п., определяющих характеристики состояний объекта
моделирования, а через них и выходные значения параметров реакции, в зависимости от значений
параметров объекта-оригинала, входных воздействий, начальных и граничных условий, а также
времени.
Математическая модель представляет собой формализованное описание системы (или
операции) с помощью некоторого абстрактного языка, например в виде совокупности математических
соотношений или схемы алгоритма. По большому счету, любое математическое выражение, в котором
фигурируют физические величины, можно рассматривать как математическую модель того или иного
процесса или явления. В частности, известное всем еще из школы уравнение S = Vt, представляет собой
модель равномерного прямолинейного движения.

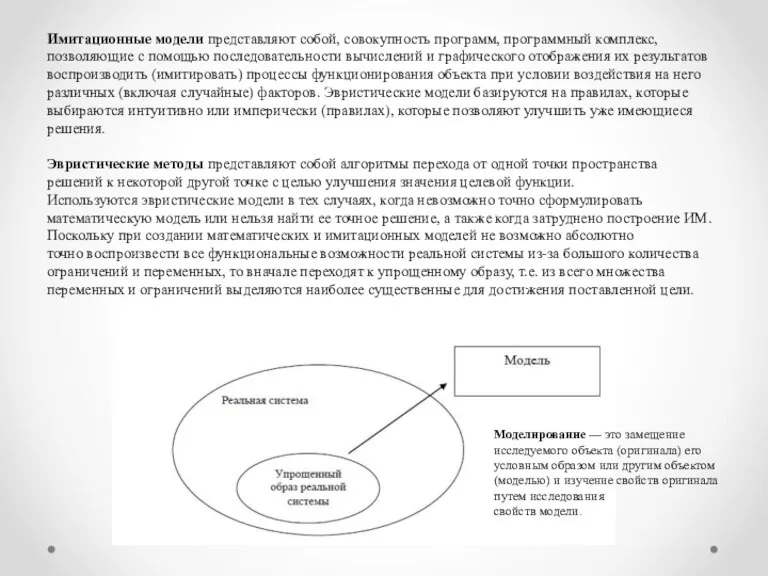
Имитационные модели представляют собой, совокупность программ, программный комплекс,
позволяющие с помощью последовательности вычислений и графического отображения их результатов
воспроизводить (имитировать) процессы функционирования объекта при условии воздействия на него
различных (включая случайные) факторов. Эвристические модели базируются на правилах, которые
выбираются интуитивно или имперически (правилах), которые позволяют улучшить уже имеющиеся
решения.
Эвристические методы представляют собой алгоритмы перехода от одной точки пространства
решений к некоторой другой точке с целью улучшения значения целевой функции.
Используются эвристические модели в тех случаях, когда невозможно точно сформулировать
математическую модель или нельзя найти ее точное решение, а также когда затруднено построение ИМ.
Поскольку при создании математических и имитационных моделей не возможно абсолютно
точно воспроизвести все функциональные возможности реальной системы из-за большого количества
ограничений и переменных, то вначале переходят к упрощенному образу, т.е. из всего множества
переменных и ограничений выделяются наиболее существенные для достижения поставленной цели.
Моделирование — это замещение исследуемого объекта (оригинала) его условным образом или другим объектом (моделью) и изучение свойств оригинала путем исследования
свойств модели.

2. Принципы построения моделей
Принцип информационной достаточности.
Принцип осуществимости.
Принцип множественности моделей.
Принцип агрегирования.
Принцип параметризации.

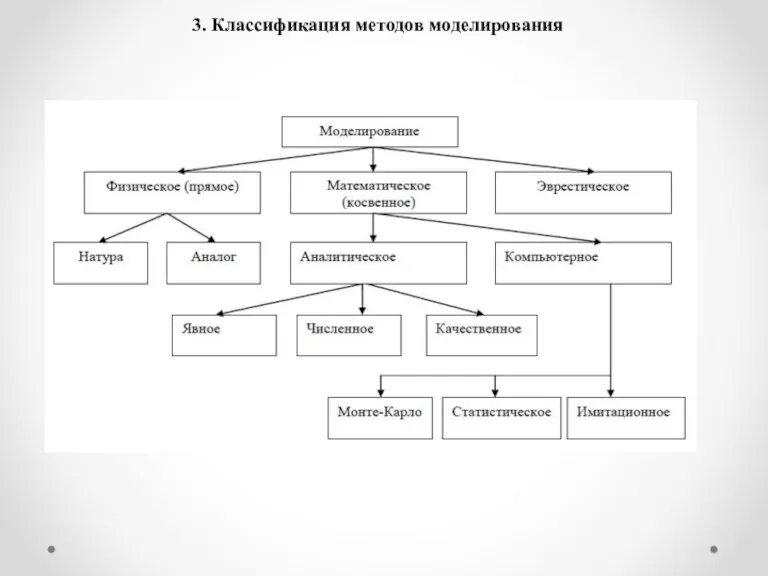
3. Классификация методов моделирования

Отметим преимущества ИМ в плане целесообразности применения:
1. Не существует законченной математической постановки данной задачи, либо еще не
разработаны аналитические методы решения сформулированной математической модели. К этой
категории относятся многие модели массового обслуживания, связанные с рассмотрением очередей.
2. Аналитические методы имеются, но математические процедуры столь сложны и трудоемки,
что ИМ даст более простой способ решения задачи.
3. Аналитические решения существуют, но их реализация невозможна вследствие недостаточной
математической подготовки имеющегося персонала. В этом случае следует сопоставить затраты на
проектирование, испытания и работу на имитационной модели с затратами, связанными с
приглашением специалистов со стороны.
4. Кроме оценки определенных параметров, желательно осуществить на имитационной модели
наблюдение за ходом процесса в течение определенного периода.
5. Имитационное моделирование может оказаться единственной возможностью вследствие
трудности постановки экспериментов и наблюдения явлений в реальных условиях; соответствующим
примером может служить изучение поведения космических кораблей в условиях межпланетных
полетов.
6. Для долговременно действующих систем или процессов может понадобиться сжатие
временной шкалы. ИМ дает возможность полностью контролировать время изучаемого процесса,
поскольку явление может быть замедленно или ускоренно по желанию.
Дополнительным преимуществом ИМ можно считать широчайшие возможности его применения
в сфере образования и профессиональной подготовки. Разработка и использование имитационной модели позволяют экспериментатору видеть и «разыгрывать» на модели реальные процессы и ситуации. Это в свою очередь должно в значительной мере помочь ему понять и прочувствовать проблему, что стимулирует процесс поиска нововведений.

К недостаткам ИМ можно отнести следующее:
1. Разработка хорошей ИМ часто обходится дорого и требует много времени, а также наличия
высокоодаренных специалистов, которых в данной фирме может и не оказаться.
2. Ввиду работы со случайными данными для обеспечения точности получаемых результатов
необходимо производить многочисленные прогоны модели, что влияет на техническое средство работы
с имитационной моделью.
3. Имитационная модель в принципе не точна, и мы не в состоянии измерить степень этой неточности. Это затруднение может быть преодолено лишь частично путем анализа чувствительности модели к изменению определенных параметров._
Идея ИМ одинакова привлекательна и для руководителей и для исследователей систем благодаря своей простоте. Поэтому метод ИМ в настоящее время стремятся применить для решения практически каждой задачи, с которой приходится сталкиваться на практике.

Что это такое?
Имитационное моделирование (симуляция) – это распространенная разновидность аналогового моделирования, реализуемого с помощью набора математических средств, специальных компьютерных программ-симуляторов и особых IT, позволяющих создавать в памяти компьютера процессы-аналоги, с помощью которых можно провести целенаправленное исследование структуры и функций реальной системы в режиме ее «имитации», осуществить оптимизацию некоторых ее параметров.

Что отражает ИМ?
Имитационная модель должна отражать логику и закономерности поведения моделируемого объекта во времени (временная динамика) и пространстве (пространственная динамика).
Имитационная модель создается:
для управления сложными бизнес-процессами, чтобы определить их характерные особенности;
при проведении экспериментов над объектами в экстренных ситуациях, связанных с рисками, в случаях, когда натуральное моделирование нежелательно или невозможно.

Типовые примеры имитационных моделей
Моделирование процессов логистики для определения временных и стоимостных параметров;
Управление размещением предприятий, оказывающих однородные услуги;
Управление процессом реализации инвестиционного проекта на различных этапах его жизненного цикла с учетом возможных рисков;
Прогнозирование финансовых результатов деятельности предприятия

Типовые примеры имитационных моделей
Бизнес-реинжиниринт несостоятельного предприятия (изменение структуры и ресурсов);
Анализ работы автотранспортных предприятий;
Моделирование обслуживания клиентов предприятиями сферы услуг;
Модели работы информационных систем и сложных вычислительных систем (аналоги с устройствами обслуживания клиентов);
И т.д.

Программное обеспечение
Особенные характеристики программного обеспечения имитационного моделирования:
Способность моделирования и отслеживание в общем модельном времени различных потоков (материальных, информационных, денежных и пр.);
Возможность уточнения параметров и ведения экстремального эксперимента.

Виды программного обеспечения
Пакет программ Microsoft Office (особенно, Excel) часто используют для проведения расчетов имитационной модели;
Система GPSS (General Purpose Simulation System) (1967 г) используется в основном для моделирования систем массового обслуживания;
Специальные современные имитационные пакеты, реализующие разные подходы к моделированию и имеющие средства визуализации (например, AnyLogic).

Истоки имитационного моделирования
Имитационное моделирование возникло для поддержки решения и исследования задач массового обслуживания (задачи об очередях).
Цель исследования очередей – оптимизация издержек:
Что выгоднее, принять на работу несколько сотрудников, чтобы уменьшить время ожидания клиентов в очереди, либо сэкономить на заработной плате сотрудников, уменьшив их количество.

Система массового обслуживания
В системе массового обслуживания каждая заявка проходит несколько этапов:
1) появление заявки на входе в систему;
2) ожидание в очереди;
3) процесс обслуживания, после которого заявка покидает систему.
Первый и третий этап характеризуются случайными величинами.

Появление заявок
Обычно заявки появляются в заданном темпе (например, два клиента в час или четыре грузовика в минуту). В этом случае для его характеристики используют дискретное распределение Пуассона:
где р (х) — вероятность поступления х заявок в единицу времени;
х — число заявок в единицу времени;
λ — среднее число заявок в единицу времени (темп по­ступления заявок);

Характеристики очереди
При моделировании очереди нужно учесть:
Длину очереди;
Правило обслуживания (например, FIFO (англ. first in, first out — «первым пришёл — первым ушёл») , или очередь с приоритетами);
В более сложных случаях, можно моделировать извлечение заявки из очереди без обслуживания, когда время ожидания превысило определенный уровень.

Обслуживание заявок
Конфигурация системы обслуживания:
Одноканальная или многоканальная система обслуживания;
Однофазное или многофазная система обслуживания;
Случайное или детерминированное время обслуживания.
Если время обслуживания является случайной величиной, часто оно подчиняется экспоненциальному закону распределения:
F(t) = p(τ< t) =1 – е–tμ, где р (τ < t) — вероятность того, что фактическое время τ обслу­живания заявки не превысит заданной величи­ны t;
μ — среднее число заявок, обслуживаемых в единицу времени.

Модели массового обслуживания
Модель А — модель одноканальной системы массового обслуживания с пуассоновским входным потоком заявок и экспоненциальным временем обслуживания.
Модель В — многоканальная система обслуживания. В многоканальной системе для обслуживания открыты два ка­нала или более. Предполагается, что клиенты ожидают в общей очереди и обращаются в первый освободившийся канал обслужи­вания;
Модель С — модель с постоянным временем обслуживания;
Модель D — модель с ограниченной популяцией;
Модель Е — модель с ограниченной очередью. Модель от­личается от предыдущих тем, что число мест в очереди ограни­чено. В этом случае заявка, прибывшая в систему, когда все ка­налы и места в очереди заняты, покидает систему необслуженной, т.е. получает отказ.

Модель массового обслуживания
Смоделируем работу парикмахерской в терминах модели массового обслуживания.
Имеется обслуживающее устройство – парикмахер;
Имеется механизм формирования очереди – комната ожидания;
Имеется генератор заявок – клиенты, которые приходят в парикмахерскую.

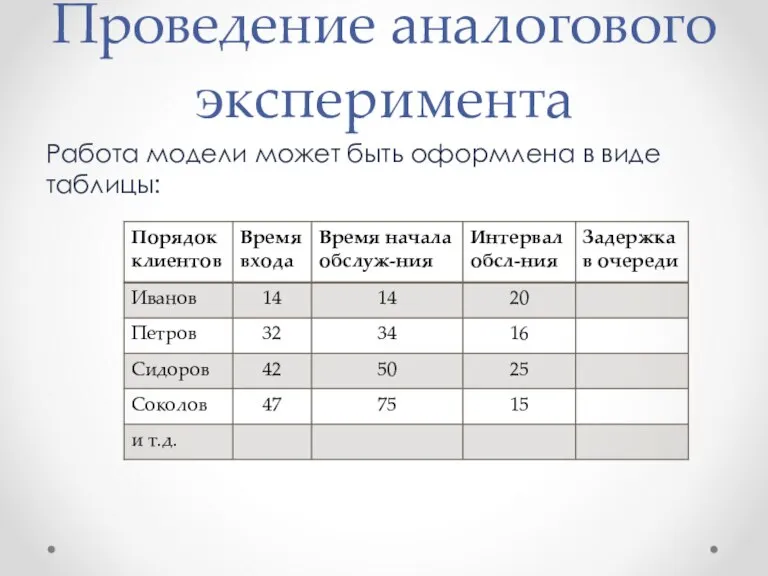
Проведение аналогового эксперимента
Работа модели может быть оформлена в виде таблицы:

Проведение аналогового эксперимента
Основные показатели, от которых зависит работа модели, определяются случайными характеристиками:
Время прихода следующего клиента;
Время обслуживания клиента парикмахером.
Основные показатели эффективности модели:
Количество клиентов в очереди;
Среднее время и отклонение ожидания клиента в очереди;
Среднее время и отклонение простоя обслуживающего устройства (парикмахера);
Количество обслуженных клиентов за день;
и т.д.

Алгоритм симуляции дискретных процессов
Узел модели – элемент, характеризующий конкретное состояние объекта модели (генератор заявок, комната ожидания, устройство обслуживания, окончание обслуживания (узел-терминатор)).
Событие – это факт перехода объекта от одного узла модели в другой.
2 типа событий:
Текущее – связано с объектом с нулевым временем;
Будущее – связано с объектом с положительными временем.
Время объекта – время, в которое для этого объекта должно произойти очередное событие.

Алгоритм симуляции дискретных процессов
Симулятор работает следующим образом:
Продвижение объектов.
По всем узлам модели ищется объект с нулевым временем и осуществляется ее продвижение на следующие узлы модели до одного из случаев:
Объект попадает во времяемкий процесс – его время меняется исходя из задержки процесса (например, обслуживание клиента);
Объект попал в очередь – очередь не пуста, или очередь пуста, но обслуживающий узел недоступен.
После продвижения очередного объекта, ищется следующий объект с нулевым временем.

Алгоритм симуляции дискретных процессов
Симулятор работает следующим образом:
2. Модификация.
Если объектов с нулевым временем нет, выбирается объект с минимальным положительным временем (с ним первым должно произойти какое либо событие).
Время этого объекта устанавливается в 0, изменяется модельное время на величину смещения и изменяются показатели времени всех других объектов модели.
После переход к стадии Продвижения объектов.

Теоретические основы – метод Монте-Карло
Этот метод называют методом статистических испытаний. Любая сложная система зависит от некоторого набора случайных факторов, имеющих различные законы распределения.
Метод Монте-Карло осуществляет многократный эксперимент и накапливает статистику его результатов.
Вероятность, что средние показатели результатов будут незначительно отличаться от показателей реальной системы, будет мала при большом количестве испытаний.

Подходы к моделированию
Агентное моделирование (моделирование поведения покупателя на рынке определенных товаров);
Модели системной динамики (основанные на моделировании потоков и переходов объектов в различные состояния);
Дискретно-событийные модели (системы массового обслуживания);
Модели пространственной динамики (пешеходные модели).

Справка по AnyLogic
https://help.anylogic.ru
Используемые полезные функции:

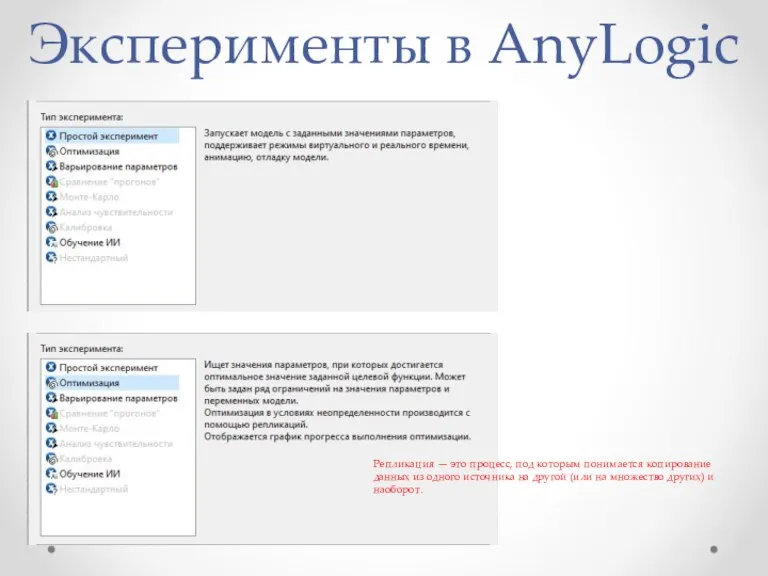
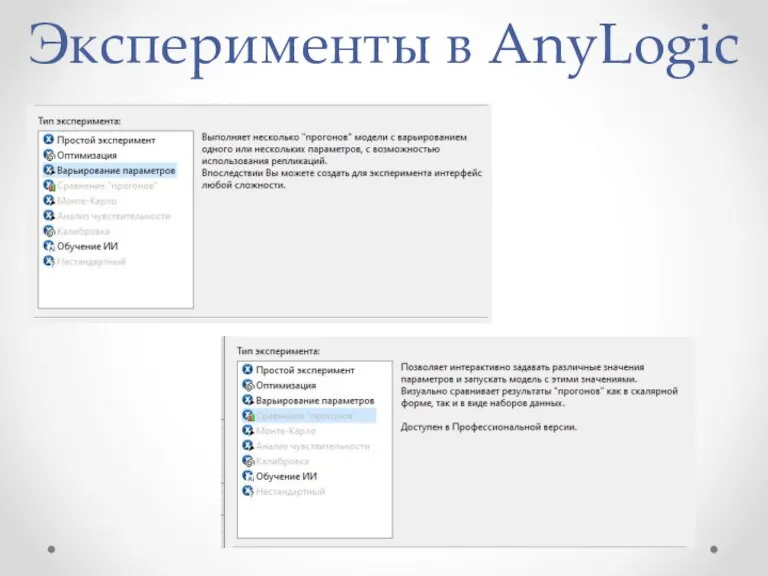
Эксперименты в AnyLogic
Репликация — это процесс, под которым понимается копирование данных из одного источника на другой (или на множество других) и наоборот.

Эксперименты в AnyLogic

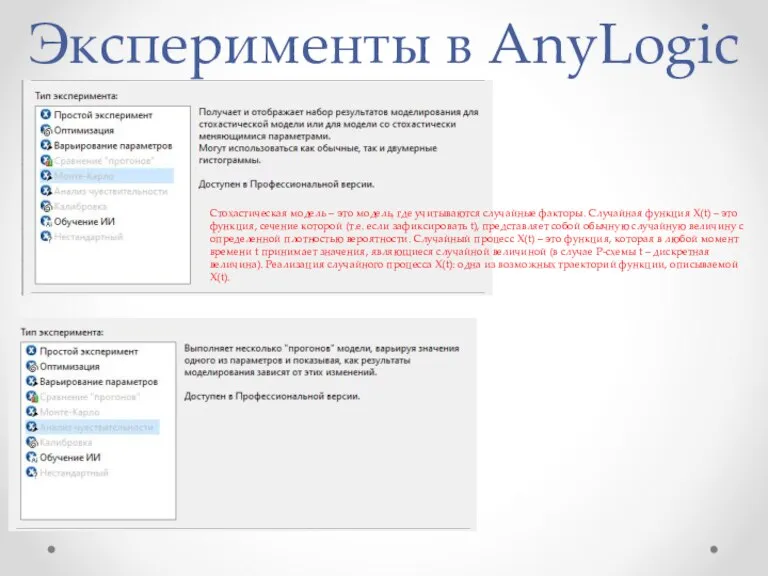
Эксперименты в AnyLogic
Стохастическая модель – это модель, где учитываются случайные факторы. Случайная функция X(t) – это функция, сечение которой (т.е. если зафиксировать t), представляет собой обычную случайную величину с определенной плотностью вероятности. Случайный процесс X(t) – это функция, которая в любой момент времени t принимает значения, являющиеся случайной величиной (в случае P-схемы t – дискретная величина). Реализация случайного процесса X(t): одна из возможных траекторий функции, описываемой X(t).