Элементы алгебры, логики, математические основы информатики

Ключевые слова
алгебра логики
высказывание
логическая операция
конъюнкция
дизъюнкция
отрицание
логическое выражение таблица истинности
законы логики

Клод Шеннон (1916-2001). Его исследования позволили применить алгебру логики в вычислительной технике
Логика
Аристотель (384-322 до н.э.). Основоположник формальной логики (понятие, суждение, умозаключение).
Джордж Буль (1815-1864). Создал новую область науки - Математическую логику (Булеву алгебру или Алгебру высказываний).

Алгебра - наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над разнообразными математическими объектами – числами, многочленами, векторами и др.
Алгебра

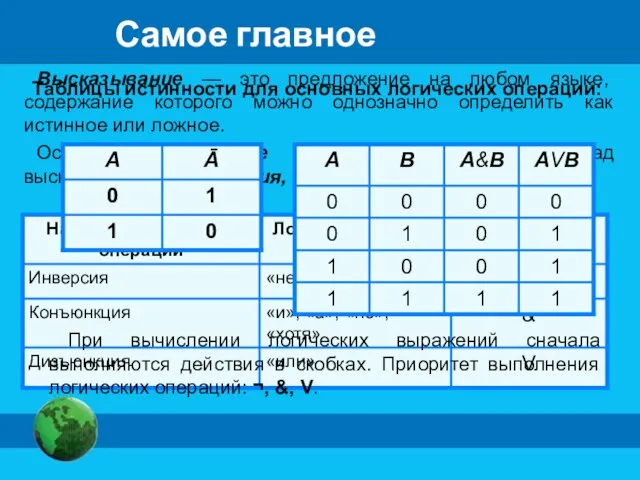
Высказывание - это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.
В русском языке высказывания выражаются повествовательными предложениями:
Земля вращается вокруг Солнца.
Москва - столица.
Побудительные и вопросительные предложения высказываниями не являются.
Без стука не входить!
Откройте учебники.
Ты выучил стихотворение?
Высказывание
Но не всякое повествовательное предложение является высказыванием:
Это высказывание ложное.

Высказывание или нет?
Зимой идет дождь.
Снегири живут в Крыму.
Кто к нам пришел?
У треугольника 5 сторон.
Как пройти в библиотеку?
Переведите число в десятичную систему.
Запишите домашнее задание

Алгебра логики определяет правила записи, вычисления значений, упрощения и преобразования высказываний.
В алгебре логики высказывания обозначают буквами и называют логическими переменными.
Если высказывание истинно, то значение соответствующей ему логической переменной обозначают единицей (А = 1), а если ложно - нулём (В = 0).
0 и 1 называются логическими значениями.
Алгебра логики

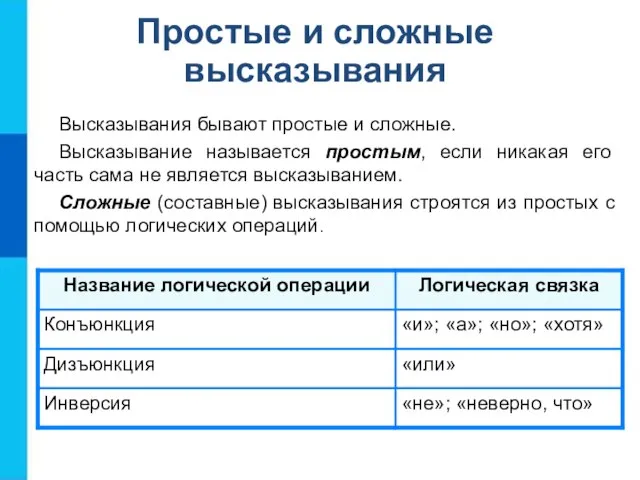
Простые и сложные высказывания
Высказывания бывают простые и сложные.
Высказывание называется простым, если никакая его часть сама не является высказыванием.
Сложные (составные) высказывания строятся из простых с помощью логических операций.

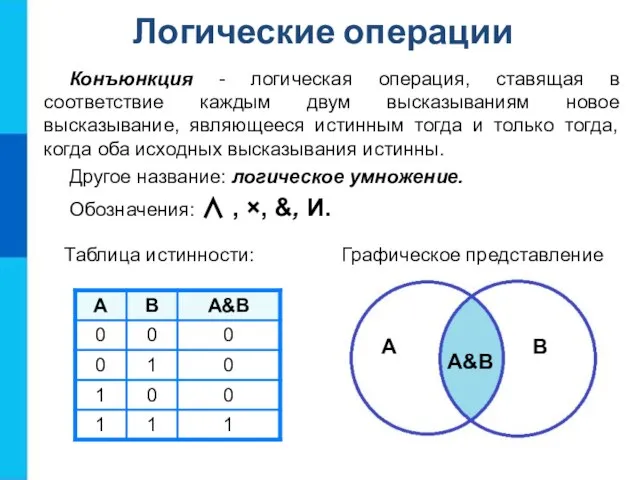
Конъюнкция - логическая операция, ставящая в соответствие каждым двум высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
Другое название: логическое умножение.
Обозначения: ∧ , ×, &, И.
Логические операции
Таблица истинности:
Графическое представление
A
B
А&В

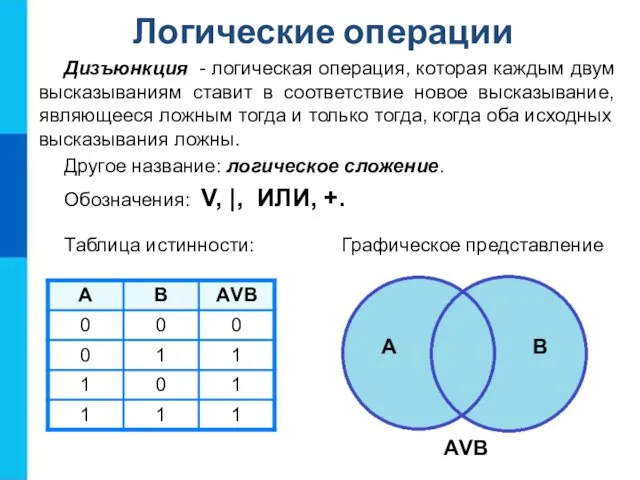
Дизъюнкция - логическая операция, которая каждым двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.
Другое название: логическое сложение.
Обозначения: V, |, ИЛИ, +.
Логические операции
Таблица истинности:
Графическое представление
A
B
АVВ

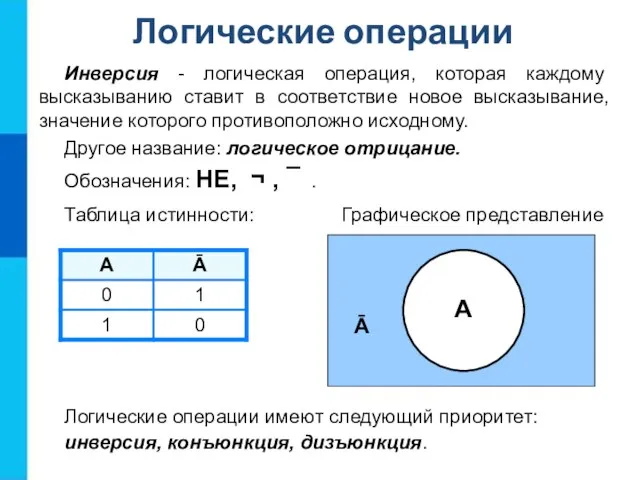
Инверсия - логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному.
Другое название: логическое отрицание.
Обозначения: НЕ, ¬ , ¯ .
Логические операции имеют следующий приоритет:
инверсия, конъюнкция, дизъюнкция.
Логические операции
Таблица истинности:
Графическое представление
A
Ā

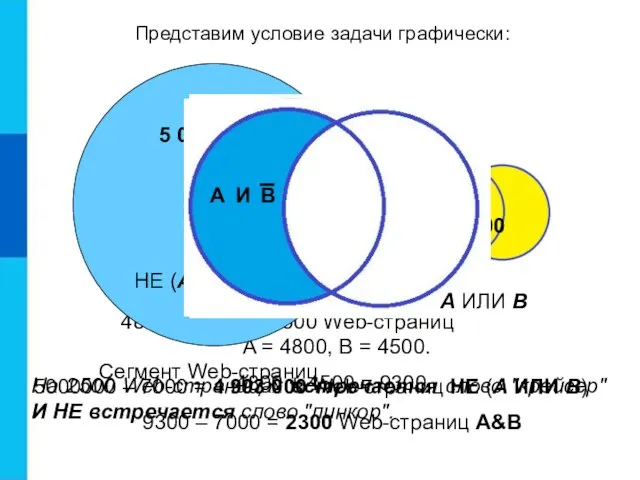
Пусть А = «На Web-странице встречается слово "крейсер"», В = «На Web-странице встречается слово "линкор"».
В некотором сегменте сети Интернет 5000000 Web-страниц. В нём высказывание А истинно для 4800 страниц, высказывание В - для 4500 страниц, а высказывание АVВ - для 7000 страниц.
Для какого количества Web-страниц в этом случае будут истинны следующие выражения и высказывание?
а) НЕ (А ИЛИ В);
б) А & B;
в) На Web-странице встречается слово "крейсер" И НЕ встречается слово "линкор".
Решаем задачу

5000000 – 7000 = 4 993 000 Web-страниц НЕ (А ИЛИ В) A = 4800, B = 4500.
4800 + 4500 = 9300
4800 – 2300 = 2500 Web-страниц
Представим условие задачи графически:
На 2500 Web-страницах встречается слово "крейсер" И НЕ встречается слово "линкор".
5 000 000
7 000
НЕ (А ИЛИ В)
Сегмент Web-страниц
A
B
A&B
9300 – 7000 = 2300 Web-страниц A&B
A
И
А ИЛИ В

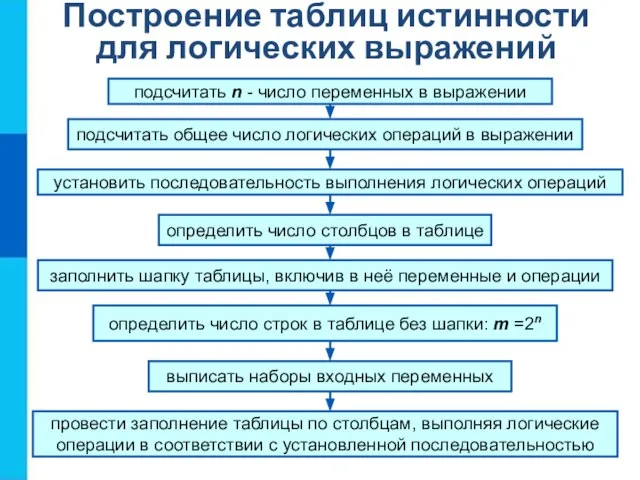
Построение таблиц истинности для логических выражений
подсчитать n - число переменных в выражении
подсчитать общее число логических операций в выражении
установить последовательность выполнения логических операций
определить число столбцов в таблице
заполнить шапку таблицы, включив в неё переменные и операции
определить число строк в таблице без шапки: m =2n
выписать наборы входных переменных
провести заполнение таблицы по столбцам, выполняя логические
операции в соответствии с установленной последовательностью

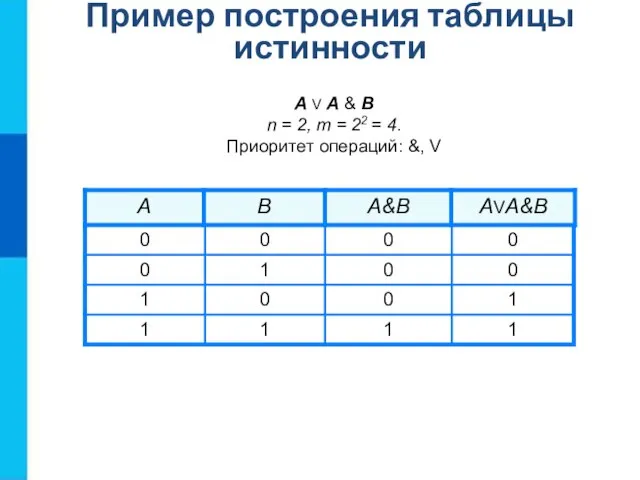
А V A & B
n = 2, m = 22 = 4.
Приоритет операций: &, V
Пример построения таблицы истинности

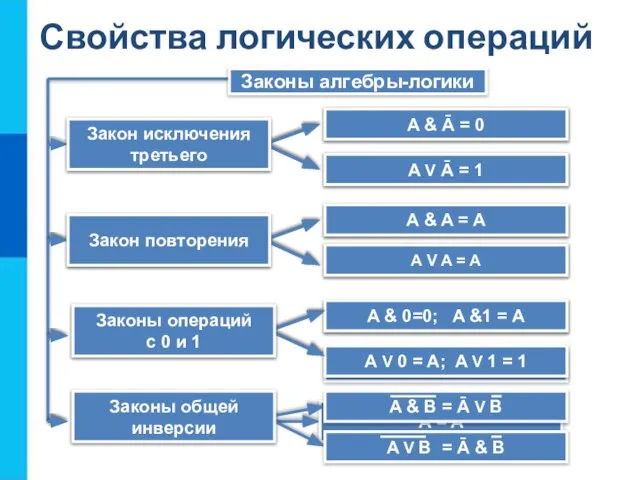
Свойства логических операций
Законы алгебры-логики
A & B = B & A
A V B = B V A
A&(BVC)= (A&B) V (A&C)
AV(B&C) = (AVB)&(AVC)
(A & B) & C = A & ( B & C)
(A V B) V C =A V ( B V C)
Переместительный
Сочетательный
Распределительный
Закон двойного
отрицания
A & Ā = 0
A V Ā = 1
A & 0=0; A &1 = A
A V 0 = A; A V 1 = 1
A & A = A
A V A = A
Закон исключения
третьего
Закон повторения
Законы операций
с 0 и 1
Законы общей
инверсии

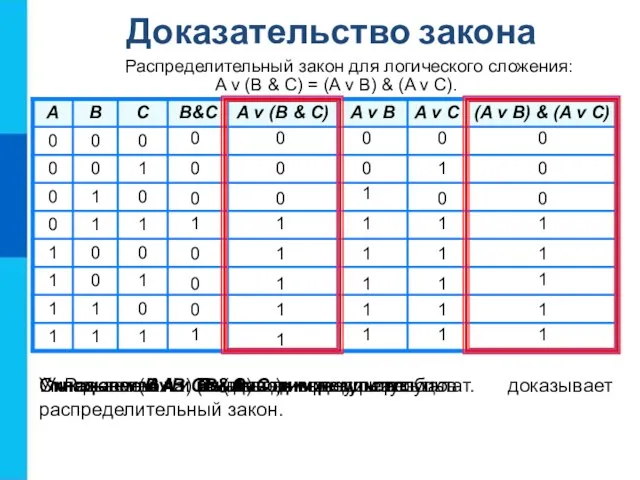
Распределительный закон для логического сложения:
A v (B & C) = (A v B) & (A v C).
Доказательство закона
Умножаем В на С и выводим результат.
0
0
0
0
0
0
1
1
Складываем А и В и выводим результат.
0
0
0
1
1
1
1
1
Складываем А и (В&С) и выводим результат.
0
0
1
1
1
1
1
1
Складываем А и C и выводим результат.
0
0
1
1
1
1
1
1
Умножаем (АvB) на (AvC )и выводим результат.
0
0
0
1
1
1
1
1
Равенство выделенных столбцов доказывает распределительный закон.

Задача. Коля, Вася и Серёжа гостили летом у бабушки. Однажды один из мальчиков нечаянно разбил любимую бабушкину вазу.
Решение логических задач
На вопрос, кто разбил вазу, они дали такие ответы:
Серёжа: 1) Я не разбивал. 2) Вася не разбивал.
Вася: 3) Серёжа не разбивал. 4) Вазу разбил Коля.
Коля: 5) Я не разбивал. 6) Вазу разбил Серёжа.
Бабушка знала, что один из её внуков (правдивый), оба раза сказал правду; второй (шутник) оба раза сказал неправду; третий (хитрец) один раз сказал правду, а другой раз - неправду. Назовите имена правдивого, шутника и хитреца.
Кто из внуков разбил вазу?

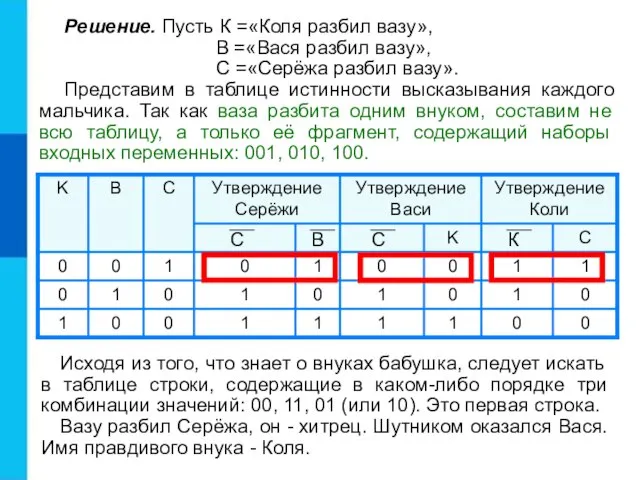
Решение. Пусть К =«Коля разбил вазу»,
В =«Вася разбил вазу»,
С =«Серёжа разбил вазу».
Представим в таблице истинности высказывания каждого мальчика. Так как ваза разбита одним внуком, составим не всю таблицу, а только её фрагмент, содержащий наборы входных переменных: 001, 010, 100.
Исходя из того, что знает о внуках бабушка, следует искать в таблице строки, содержащие в каком-либо порядке три комбинации значений: 00, 11, 01 (или 10). Это первая строка.
Вазу разбил Серёжа, он - хитрец. Шутником оказался Вася. Имя правдивого внука - Коля.

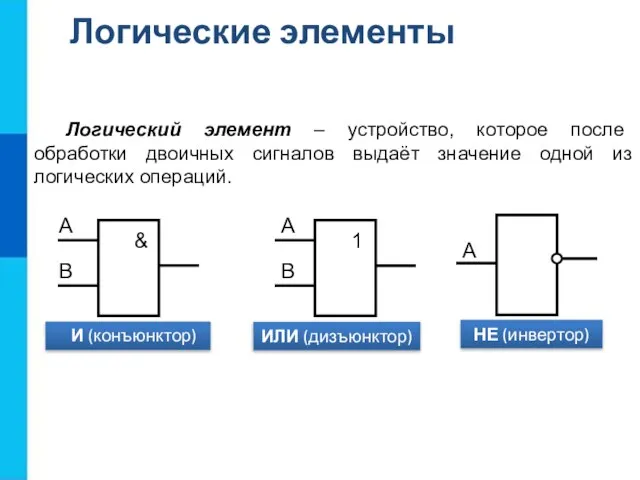
Логический элемент – устройство, которое после обработки двоичных сигналов выдаёт значение одной из логических операций.
Логические элементы

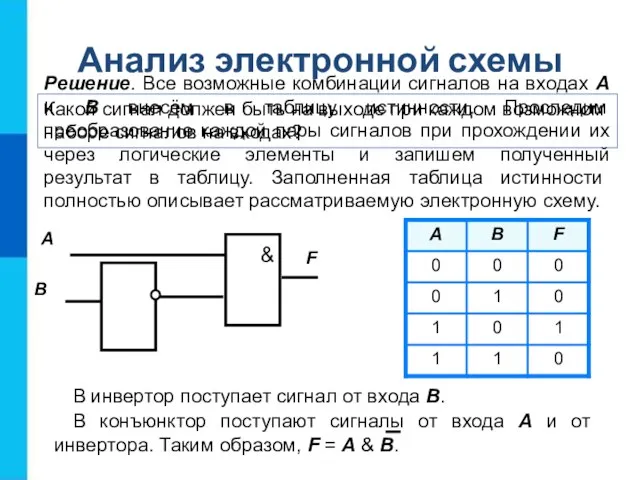
Какой сигнал должен быть на выходе при каждом возможном наборе сигналов на входах?
Анализ электронной схемы
Решение. Все возможные комбинации сигналов на входах А и В внесём в таблицу истинности. Проследим преобразование каждой пары сигналов при прохождении их через логические элементы и запишем полученный результат в таблицу. Заполненная таблица истинности полностью описывает рассматриваемую электронную схему.
А
В
В инвертор поступает сигнал от входа В.
В конъюнктор поступают сигналы от входа А и от инвертора. Таким образом, F = A & B.

Высказывание — это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.
Основные логические операции, определённые над высказываниями: инверсия, конъюнкция, дизъюнкция.
Таблицы истинности для основных логических операций:
При вычислении логических выражений сначала выполняются действия в скобках. Приоритет выполнения логических операций: ¬, &, V.
Самое главное