Формализация Тьюринга

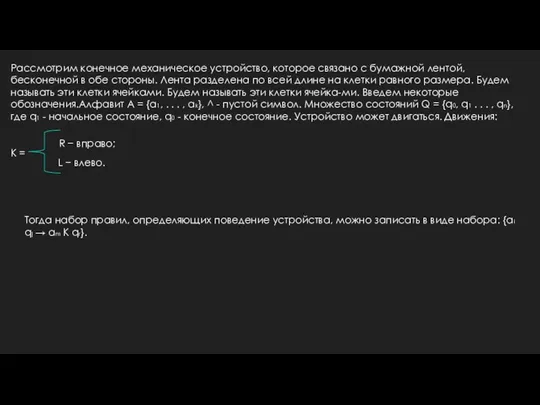
Рассмотрим конечное механическое устройство, которое связано с бумажной лентой, бесконечной в обе стороны. Лента разделена по всей длине на клетки равного размера. Будем называть эти клетки ячейками. Будем называть эти клетки ячейка-ми. Введем некоторые обозначения.Алфавит A = {α1, . . . , αk}, ^ - пустой символ. Множество состояний Q = {q0, q1 . . . , qn}, где q1 - начальное состояние, q0 - конечное состояние. Устройство может двигаться. Движения:
K =
R − вправо;
L − влево.
Тогда набор правил, определяющих поведение устройства, можно записать в виде набора: {αi qj → αm K qr}.

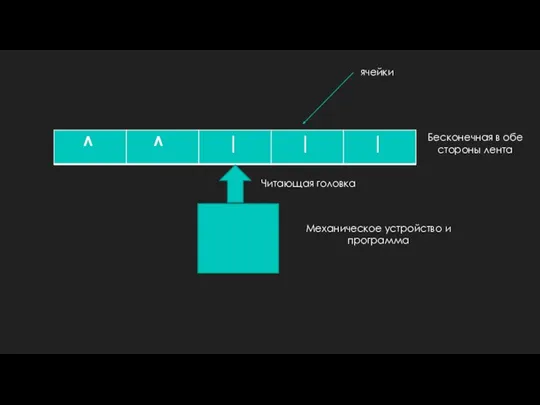
Бесконечная в обе стороны лента
ячейки
Читающая головка
Механическое устройство и программа

Читающая головка МТ обозревает очередную ячейку, на которой за-писан символ αi ∈ A. МТ находится в некотором состоянии qj ∈ Q. Берется команда из программы МТ, у которой левая часть имеет αiqj . Далее действие устройства происходит по правой части этой команды. Т. е. символ αi заменяется на символ αm. Читающая головка сдвигается влево, если K = L. Читающая головка сдвигается вправо, если K = R.

После этого МТ переходит в состояние qr ∈ Q. МТ начинает свою работу в состянии q1, завершает работу в состоянии q0. Среди символов алфави-та есть пустой символ - ∧, замена символа α на символ ∧ эквивалентно стиранию этого символа на ленте.

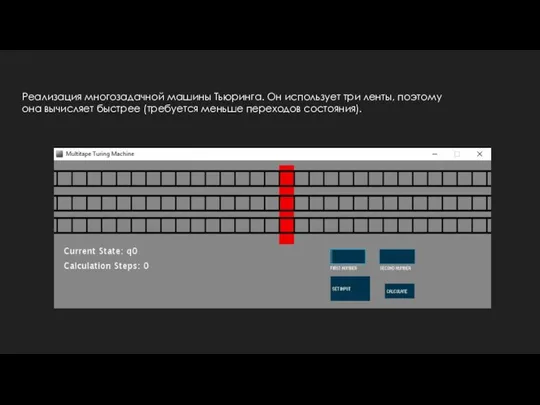
Реализация многозадачной машины Тьюринга. Он использует три ленты, поэтому она вычисляет быстрее (требуется меньше переходов состояния).

Пример. Построим МТ, вычисляющую функцию f(x) = x + 1. Число x на ленте представим, как x + 1 единица. Число 0 представляется, как одна единица. 1 представляется, как ∧ 1 1 ∧ ∧. Программа работы МТ, вычисляющей функцию f, будет следующей: