Содержание
- 2. Теорема: Бутерброд с колбасой лучше вечной любви Доказательство: Что может быть лучше вечной любви? Да ничего.
- 3. Одно из важнейших предназначений логики состоит в том, чтобы устанавливать, что из чего следует, т.е. устанавливать
- 4. Теория логического следования изучает закономерности образования формул F1, F2, …, Fk, G, по которым первые k
- 5. Понятие логического следствия Определение 1 F1, F2, …, Fk ╞ G Формула G называется логическим следствием
- 6. Понятие логического следствия F1, F2, …, Fk ╞ G Формулы F1, F2, …, Fk называются посылками
- 7. Понятие логического следствия F1, F2, …, Fk ╞ G, если для любых высказывательных переменных, при которых:
- 8. Алгоритм проверки формул на логическое следствие Построить истинностную таблицу для формул F1, F2, …, Fk и
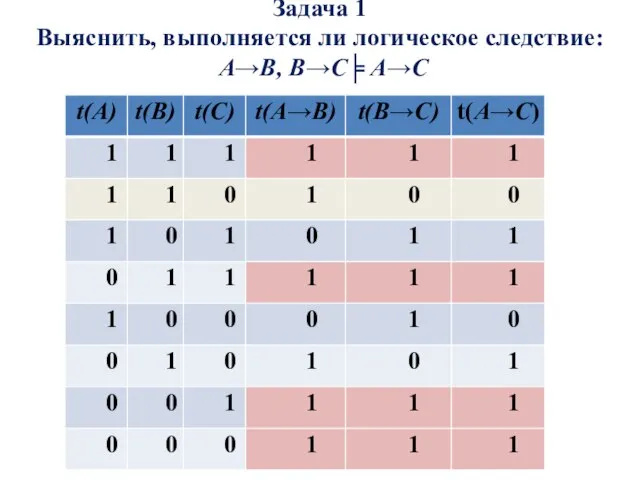
- 9. Задача 1 Выяснить, выполняется ли логическое следствие: A→B, B→C╞ A→C
- 10. Признак логического следствия Теорема 1 F1, F2, …, Fk ╞ G ⬄ ((F1˄F2˄…˄Fk)→G)-ТИ
- 11. Теорема 1 F1, F2, …, Fk ╞ G ⬄ ((F1˄F2˄…˄Fk)→G)-ТИ Доказательство (необходимость). Дано: F1, F2, …,
- 12. Теорема 1 F1, F2, …, Fk ╞ G ⬄ ((F1˄F2˄…˄Fk)→G)-ТИ Доказательство (достаточность). Дано: ((F1˄F2˄…˄Fk)→G)-ТИ Докажем: F1,
- 13. Задача 1 Выяснить, выполняется ли логическое следствие: A→B, B→C╞ A→C Решение (2 способ) по признаку логического
- 14. Свойства логического следования 1. (рефлексивное свойство логического следования) F1, F2, …,Fk╞ Fi (i=1,2,…,k)
- 15. Свойства логического следования 2. (транзитивное свойство логического следования) Если F1, F2, …, Fk╞ Hi (i=1, 2,
- 16. Свойства логического следования 3. Если {H1, H2, …, Hs} {F1, F2, …, Fk } и H1,
- 17. Свойства логического следования 4. (теорема дедукции) Если F1,F2, …,Fk-1,Fk╞G, то F1, F2, …,Fk-1╞(Fk→G)
- 18. Свойства логического следования 5. Если F1,F2, …,Fk╞G и G≡H, то F1, F2, …,Fk╞H
- 19. Свойства логического следования 6. Пусть дано множество формул F1, F2, …,Fk (1) и последовательность формул H1,
- 20. Дедуктивное рассуждение ( или вывод) – логическая операция, в результате которой из одного или нескольких взаимосвязанных
- 21. Правила логических умозаключений Правило заключения: F, F→G╞G 2. Правило силлогизма: F→G, G→H ╞ F→H 3. Правило
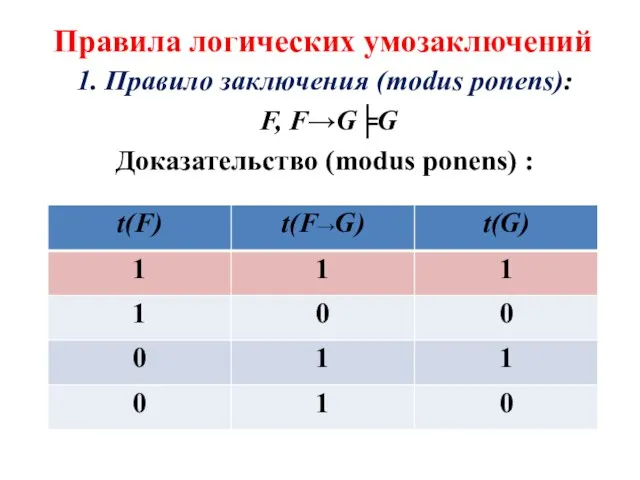
- 22. Правила логических умозаключений 1. Правило заключения (modus ponens): F, F→G╞G Доказательство (modus ponens) :
- 23. Задача 2 Выяснить, выполняется ли логическое следствие: A→B, C→D, A˅C╞B˅D Решение (3 способ) – на основе
- 24. Метод от противного Требуется выяснить: F1, F2, …, Fk ╞ G Суть метода Предположим, что G
- 25. Задача 2 Выяснить, выполняется ли логическое следование: A→B, C→D, A˅C╞B˅D Решение (4 способ) – от противного:
- 26. Анализ рассуждений Алгоритм установления справедливости рассуждения Выделить все простые высказывания, входящие в состав рассуждения, и обозначить
- 27. Задача 2 Выяснить, являются ли следующие рассуждения логически верными: Если Джонс не встречал ночью Смита, то
- 28. Решение: Введем логические переменные: А: «Джонс не встречал ночью Смита» В: «Смит убийца» С: «Джонс лжет»
- 30. Скачать презентацию

























 Делегаты в C#
Делегаты в C# Поиск информации в Интернете
Поиск информации в Интернете Информационная система ателье
Информационная система ателье 7-1-1
7-1-1 Одномерные массивы целых чисел. Алгоритмизация и программирование
Одномерные массивы целых чисел. Алгоритмизация и программирование ISDN (Integrated Services Digital Network)
ISDN (Integrated Services Digital Network) ИКТ на уроках технологии
ИКТ на уроках технологии Разработка сайта Общества с ограниченной ответственностью “Петраколор”
Разработка сайта Общества с ограниченной ответственностью “Петраколор” Информационные модели на графах. Деревья
Информационные модели на графах. Деревья Функции электронных таблиц. Построение диаграмм. Решение задач средствами MS Excel
Функции электронных таблиц. Построение диаграмм. Решение задач средствами MS Excel Система Генеральные директор для руководителей
Система Генеральные директор для руководителей Новсти мира
Новсти мира Что такое программирование
Что такое программирование Useful invention. E-reader
Useful invention. E-reader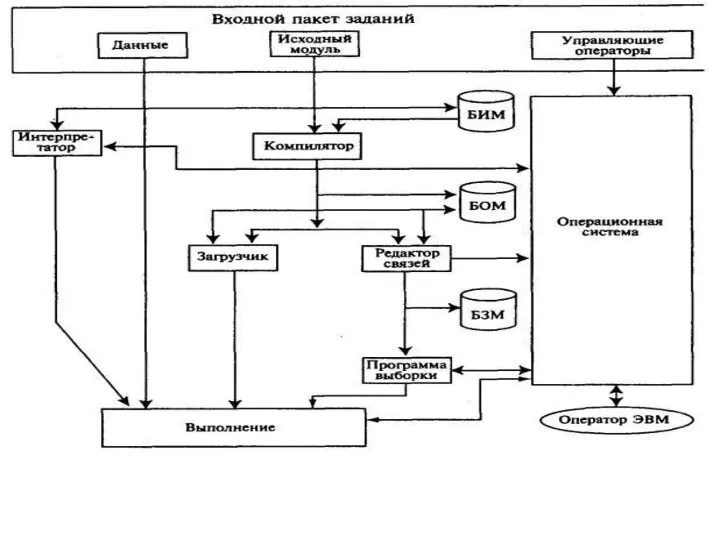 Входной пакет заданий
Входной пакет заданий Логика. Подготовка к ГИА по информатике
Логика. Подготовка к ГИА по информатике JS. JavaScript — мультипарадигменный язык программирования
JS. JavaScript — мультипарадигменный язык программирования Компьютерная графика
Компьютерная графика Сотрудничество семьи и школы в интересах детей
Сотрудничество семьи и школы в интересах детей Наука, изучающая способы хранения, передачи, обработки информации
Наука, изучающая способы хранения, передачи, обработки информации Инди-игры
Инди-игры Sem1_01_intro_to_ide_2223
Sem1_01_intro_to_ide_2223 Квалификационная работа: Синтез и анализ нечетких регуляторов Сугено первого порядка при изменении параметров объекта управления
Квалификационная работа: Синтез и анализ нечетких регуляторов Сугено первого порядка при изменении параметров объекта управления Особенности конструкции НЖМД, виды дефектов магнитного диска НЖМД
Особенности конструкции НЖМД, виды дефектов магнитного диска НЖМД Выравнивание текста в документе Microsoft Word. Урок 5
Выравнивание текста в документе Microsoft Word. Урок 5 Процедурное программирование 01_09_2021
Процедурное программирование 01_09_2021 Технология создания цифровой мультимедийной информации
Технология создания цифровой мультимедийной информации