Содержание
- 2. Формула Шеннона для пропускной способности гауссовского канала: В реальности спектральная плотность мощности шума N0 может зачастую
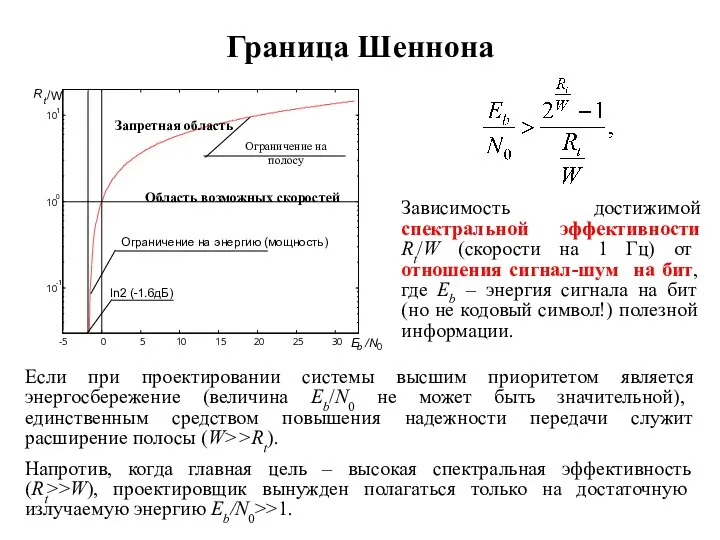
- 3. Граница Шеннона Зависимость достижимой спектральной эффективности Rt/W (скорости на 1 Гц) от отношения сигнал-шум на бит,
- 4. Важнейшие границы теории кодирования. Граница Хэмминга Теорема Любой двоичный код, исправляющий вплоть до t ошибок, удовлетворяет
- 5. Совершенные коды Коды, лежащие на границе Хэмминга (удовлетворяющие ей с равенством), называются совершенными. Совершенные коды исправляют
- 6. Пример Пусть Граница Хемминга дает следующий результат: Таким образом, возможно построение кода с параметрами (n, k)
- 7. Совершенные коды Геометрически такие коды реализуют так называемую «плотную упаковку», при которой все 2n двоичных векторов
- 8. Код Голея Сфера – принадлежит ровно n-мерных векторов Заметим, что Гипотеза: 23-мерное двоичное пространство можно плотно
- 9. Код Голея В основе конструкции кода лежит разложение x23 – 1 = (1 + x) g1(x)
- 10. Порождающая матрица кода Голея (23, 12)
- 11. Граница Варшамова–Гилберта Если k = log M целое число, эта граница модифицируется в более точную границу
- 12. Асимптотические версии Если n>>1, код не существует при нарушении любого из неравенств (асимптотические границы Хэмминга и
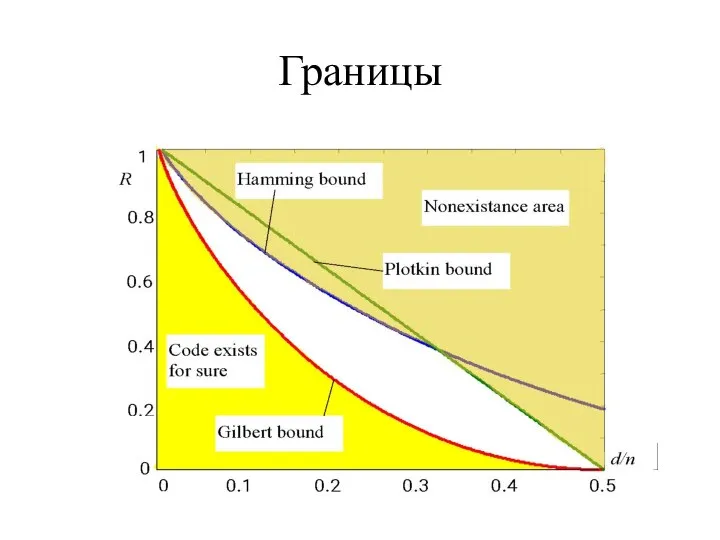
- 13. Границы
- 14. Комментарии Коды с параметрами M, n, d, попадающими в область выше любой из границ Хэмминга или
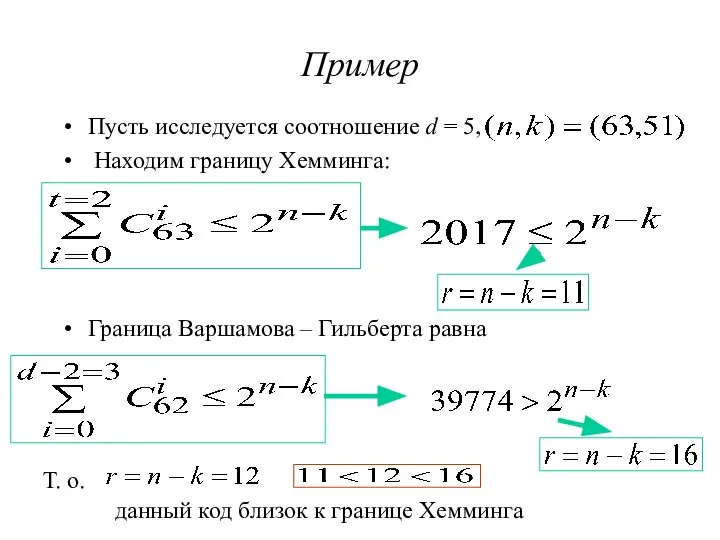
- 15. Пример Пусть исследуется соотношение d = 5, Находим границу Хемминга: Граница Варшамова – Гильберта равна Т.
- 16. Hamming Bound > HB := proc(n,d) local b,i,t,sum: t := floor((d-1)/2): sum := 1: for i
- 17. Gilbert-Varshamov Bound, version 1 > GV1 := proc(n,d) local b,i,sum: sum := 1: for i from
- 18. Gilbert-Varshamov Bound, version 2 > GV2 := proc(n,d) local i,b,sum: sum := 1: for i from
- 19. Singleton Bound SB := proc(n,d): > printf("k is at most %d",n-d+1): > end: Пример > SB(7,3);
- 20. Пример > SB(7,3); k is at most 5 HB(7,3);k is at most 4 > GV1(7,3); There
- 21. Источники сообщений, количество информации, энтропия Идея определения количества информации С теоретической точки зрения любая универсально применимая
- 22. Математическая модель источника информации. Дискретные источники Дискретным называется источник, множество X возможных сообщений которого конечно или
- 23. Непрерывные источники Рассматривая непрерывные источники, мы ограничимся только теми, несчетный ансамбль которых может быть ассоциирован с
- 24. Количество информации в сообщении Аксиомы количества информации (требования к универсальной информационной мере): Количество информации в сообщении
- 25. Хартли Единственной функцией, удовлетворяющей этим трем аксиомам оказывается логарифм вероятности сообщения Единица измерения количества информации зависит
- 26. Энтропия дискретного источника Энтропия дискретного источника есть среднее количество информации в его сообщениях: Свойства энтропии: Энтропия
- 27. Свойства энтропии: Энтропия ограничена сверху соотношением Энтропия ансамбля пар сообщений, генерируемых двумя независимыми источниками аддитивна
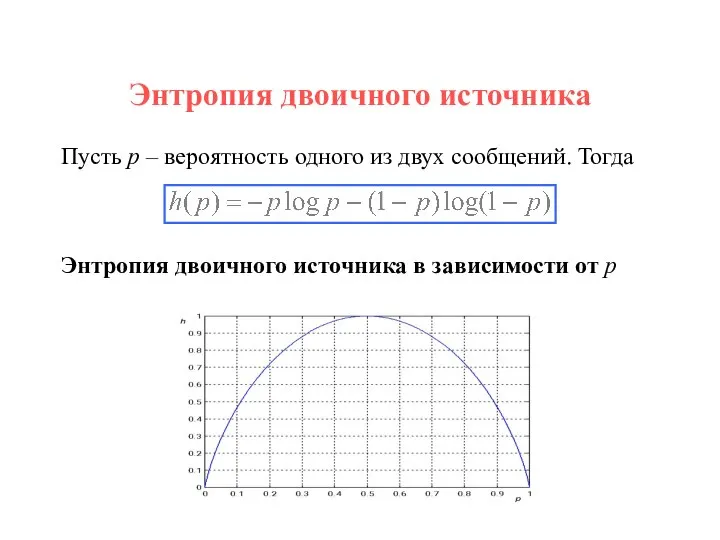
- 28. Энтропия двоичного источника Пусть p – вероятность одного из двух сообщений. Тогда Энтропия двоичного источника в
- 30. Скачать презентацию























 Pairwise. Тестирование пар значений
Pairwise. Тестирование пар значений Возможности голосового помощника Маруся в организации
Возможности голосового помощника Маруся в организации Улучшаем монетизацию c РСЯ
Улучшаем монетизацию c РСЯ Программирование линейных алгоритмов. Начала программирования
Программирование линейных алгоритмов. Начала программирования Графическая модель издания. Часть 4
Графическая модель издания. Часть 4 Ruby - язык программирования
Ruby - язык программирования Bazele promovării produselor software
Bazele promovării produselor software RPC в NodeJS
RPC в NodeJS Кодирование информации
Кодирование информации Программирование в Lego Wedo 2.0
Программирование в Lego Wedo 2.0 Название приложения. Название кейса. Название команды. ФИО участников. Название МБУ (шаблон)
Название приложения. Название кейса. Название команды. ФИО участников. Название МБУ (шаблон) Представление информации в форме таблиц
Представление информации в форме таблиц IT Школа Samsung. Производственная гимнастика!
IT Школа Samsung. Производственная гимнастика! Исполнитель Робот. Сложные условия
Исполнитель Робот. Сложные условия Монтаж. Этапы
Монтаж. Этапы Текстовые документы и технологии их создания. Обработка текстовой информации
Текстовые документы и технологии их создания. Обработка текстовой информации Сетевой этикет
Сетевой этикет Приложение-коробка для корпоративных мероприятий
Приложение-коробка для корпоративных мероприятий Что такое gimp?
Что такое gimp? Необычные изобретения XX и XXI века
Необычные изобретения XX и XXI века Web-конструирование. Практическое занятие. Создание многостраничного сайта. 2 занятие
Web-конструирование. Практическое занятие. Создание многостраничного сайта. 2 занятие Презентация _Как устроен персональный компьютер_ (7 класс)
Презентация _Как устроен персональный компьютер_ (7 класс) Инициализация и разрушение объектов
Инициализация и разрушение объектов Библиотека в социальных сетях
Библиотека в социальных сетях Основы информационно-культурной грамотности
Основы информационно-культурной грамотности Схематичное расположение
Схематичное расположение Стилевое форматирование
Стилевое форматирование Основы современных информационных технологий
Основы современных информационных технологий