Huffman coding (student’s supervised self study work)

Huffman coding
Given symbols and their frequencies, our goal is to construct a rooted binary tree where the symbols are the labels of the leaves.
The algorithm begins with a forest of trees each consisting of one vertex, where each vertex has a symbol as its label and where the weight of this vertex equals the frequency of the symbol that is its label.

Huffman coding
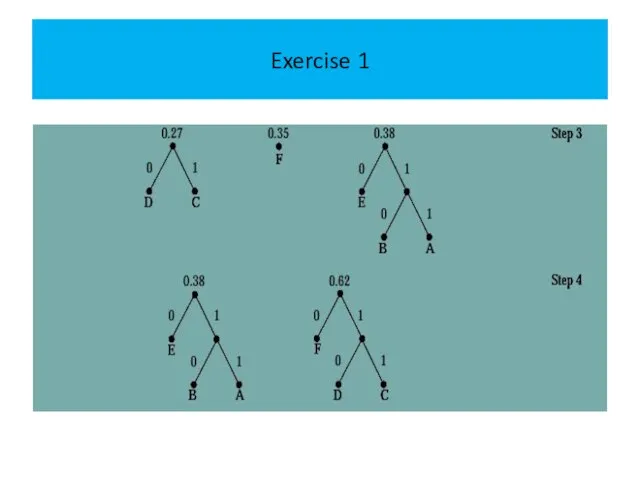
At each step, we combine two trees having the least total weight into a single tree by introducing a new root and placing the tree with larger weight as its left subtree and the tree with smaller weight as its right subtree.
Furthermore, we assign the sum of the weights of the two subtrees of this tree as the total weight of the tree. (Although procedures for breaking ties by choosing between trees with equal weights can be specified, we will not specify such procedures here.)

Huffman coding
The algorithm is finished when it has constructed a tree, that is, when the forest is reduced to a single tree.

Exercise 1
Use Huffman coding to encode the following symbols with the frequencies listed: A: 0.08, B: 0.10, C: 0.12, D: 0.15, E: 0.20, F: 0.35. What is the average number of bits used to encode a character?

Exercise 1
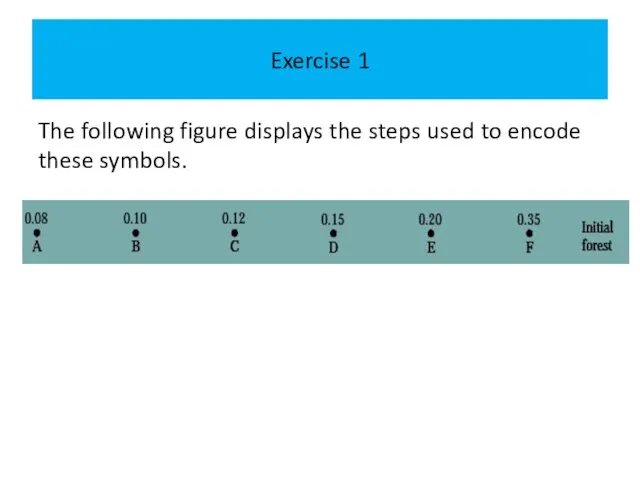
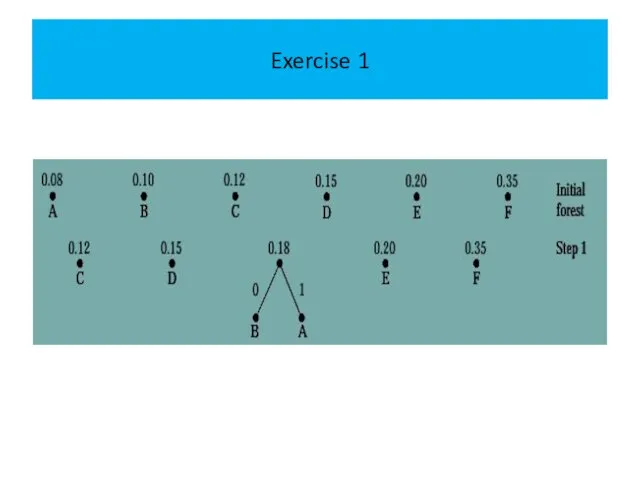
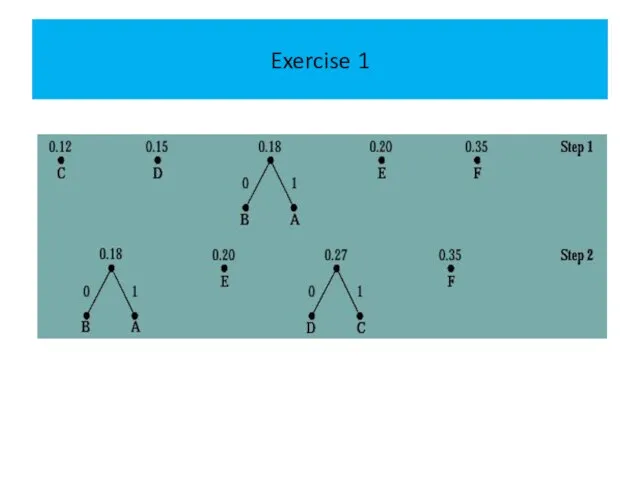
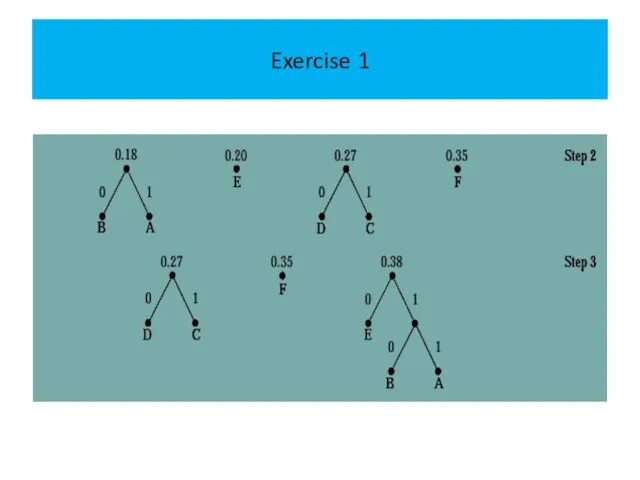
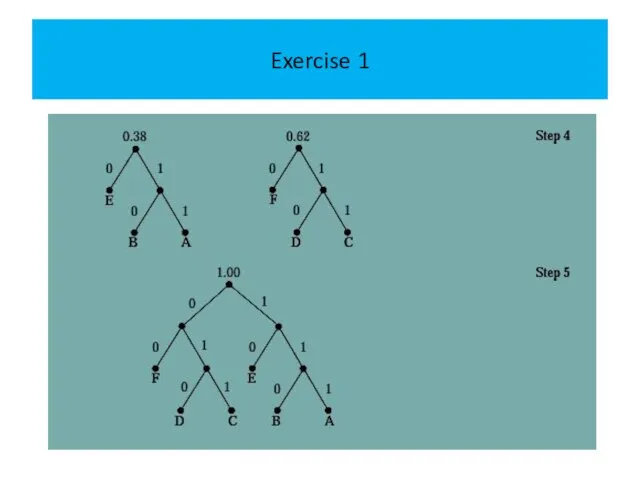
The following figure displays the steps used to encode these symbols.

Exercise 1

Exercise 1

Exercise 1

Exercise 1

Exercise 1

Exercise 1
The encoding produced encodes A by 111, B by 110, C by 011, D by 010, E by 10, and F by 00.
The average number of bits used to encode a symbol using this encoding is
3·0.08+3·0.10+3·0.12+3·0.15+2·0.20+2·0.35=2.45

Exercise 2
Use Huffman coding to encode these symbols with given frequencies: A: 0.10, B: 0.25, C: 0.05, D: 0.15, E: 0.30, F: 0.07, G: 0.08.
What is the average number of bits required to encode a symbol?

Exercise 3