Информатика и информация

Перечень основной и дополнительной литературы по курсу «Информатика»
Основная литература:
М. Брой «Информатика. Основополагающее введение» т.1 М. Диалог-Мифи, 1996
С. Лавров «Программирование, математические основы, средства, теория» из-во БХВ – Петербург, 2001
С. Алагич, М. Арбиб «Проектирование корректных, структурированных программ», М. Радио и Связь, 1994
Е.А. Андреева, Л.Л. Босова, И.Н. Фалина «Математические основы информатики», из-во «Бином», М., 2005
Н. Вирт «Алгоритмы + структуры данных = программы», М., Мир
Б. Страуструп «Язык программирования С++», из-во «Бином», М., 1999
Т.А. Павловская «С/С++ Программирование на языке высокого уровня», СПБ Питер 2006
О

Перечень основной и дополнительной литературы
Основная литература
Г. Буч «Объектно-ориентированный анализ и проектирование с примерами приложений на С++», Санкт-Петербург, «Бином», 1998
В.Н. Пильщиков «Ассемблер», М. Диалог-Мифи, 1996
С.В. Зубков «Ассемблер – язык неограниченных возможностей», М., ДМК., 1999
Дополнительная литература:
Дж. Глен Брукшир «Введение в компьютерные науки», из-во «Вильямс»», Москва, Санкт-Петербург, Киев, 2001
Т. Пратт, М. Зелковиц «Языки программирования, разработка и реализация», из-во Питер, 2002
Д. Кнут «Искусство программирования», М.,
С. Окулов «Программирование в алгоритмах», Из-во «Бином», Москва, 2002
Е.В. Кудрина, М.В. Огнева «Программирование на С/С++», изд. Центр «Наука», 2009

Перечень основной и дополнительной литературы по курсу «Информатика»
а) основная литература:
«Информатика. Базовый курс» : М.; СПб. и др., Питер, 2010
Огнева М.В., Кудрина Е.В. «Основы программирования на С++ часть 1». Издательский центр Наука, 2008
Огнева М.В., Кудрина Е.В. «основы программирования на С++ часть 2». Издательский центр Наука, 2009
Павловская, Т. А., Щупак Ю. А «C/C++. Структурное и объектно-ориентированное программирование : практикум» : М.; СПб. и др., Питер, 2010
Бройдо В.Л., Ильина О.П. «Архитектура ЭВМ и систем», учеб. для вузов . -2-е изд., М.; СПб. и др., Питер, 2009
б) дополнительная литература:
М. Брой «Информатика. Основополагающее введение» т.1 М. Диалог-Мифи, 1996
С. Лавров «Программирование, математические основы, средства, теория» из-во БХВ – Петербург, 2001
С. Алагич, М. Арбиб «Проектирование корректных, структурированных программ», М. Радио и Связь, 1994

Добполнительная литература
Макконелл Дж. « Основы современных алгоритмов» учеб. пособие по направлению подготовки специалистов "Информатика и вычислительная техника" . -2-е доп. изд., М.: Техносфера, 2004
Павловская Т.А «C/C++. Программирование на языке высокого уровня», М.; СПб. и др., Питер, 2010
Огнёва М.В., Фёдорова А.Г., Шуринова Е.В. «Основы информационных технологий» «Научная книга» 2003.
Информатика. Базовый курс : учеб. пособие . -2-е изд., М.; СПб. и др., Питер, 2008, Серия: Учебник для вузов
Вирт Н. «Алгоритмы и структуры данных», из-во Невский диалект, 2005
Окулов С.М. «Программирование в алгоритмах», учебное пособие : М.: БИНОМ. Лаб. знаний, 2004
Круз Р.Л. «Структуры данных и проектирование программ», учеб. пособие, М.: БИНОМ. Лаб. знаний, 2008

Информатика – это наука о сборе, накоплении, хранении, обработке, передаче и использовании информации.
Она занимается формализованным представлением информации и ее обработкой, включает в себя вопросы анализа и моделирования взаимосвязей и структур в самых различных областях науки, техники и производства.
Формирование моделей определенных структур объектов, взаимодействий и процессов в какой-либо предметной области осуществляется с помощью таких формальных средств, как структуры данных, языки программирования, логические формулы.
Понятие информации является основополагающим, фундаментальным, но следует различать:
Формальное представление, изображение информации – ее внешнюю форму
Абстрактное значение, содержание, семантику изображения
Связь абстрактной информации с реальным миром

В информатике тесно связаны между собой формальное представление информации и предписания по ее обработке, а также формальное описание этих правил и процессов…
Информатика – наука, или искусство?....
Информацией обычно называют содержательное значение, семантику некоторого высказывания, описания, сообщения.
Для ее машинного представления существуют различные формы:
условные знаки, сигналы;
акустическое, речевое представление;
графическое представление – рисунки, пиктограммы;
текстовое представление с помощью последовательности символов.
Интерпретируя представление информации, получаем ее абстрактное значение, семантику.
Для обмена информацией должны существовать согласованные, единые системы ее представления и интерпретации. …..

В информатике интерпретацию представления информации отождествляют с подходящими математическими структурами и тогда для ее обработки используют математические методы.
В приложениях информатики может быть рассмотрено точно описанное множество представлений информации R с интерпретацией I в множестве элементов информации – А.
Интерпретация I данному представлению сообщения r ставит в соответствие некоторое абстрактное информационное содержание I(r). Таким образом, интерпретации соответствует отображение I : R A
Информационную систему можно обозначить тройкой
(A, R, I)
Система представлений R должна быть конечной. Пример.
Пусть N – система натуральных чисел, включая число ноль –это есть последовательность штрихов:
ε, /, //, ///, ////, ///// и т.д
Здесь ε - пустая последовательность.

Общепринятым представлением целых чисел есть последовательность из символов множества {0,1,2,3,4,5,6,7,8,9}
Интерпретацией I будет отображение десятичного представления чисел в последовательности штрихов.
I : {0,1,2,3,4,5,6,7,8,9}+ ? N, где
{0,1,2,3,4,5,6,7,8,9}+ - множество непустых конечных последовательностей десятичных цифр. Например,
I{0} = ε, I{1} = /, I{2} = //, I{3} = ///, и т.д.
Информация в ее абстрактном смысле может быть только представлена. Понятие числа в математике никак не зависит от способа его представления. Но способы представления существенно различны с точки зрения удобства реализации процессов обработки.
В одной системе представления возможны различные изображения одной и той же информации.

В информационной системе (A,R,I) два изображения r1 и r2 называются семантически эквивалентными, если они несут одинаковую абстрактную информацию I(r1) = I(r2)
Простейший пример информационной системы , которая является фундаментальной как в математике, так и в информатике, является логика высказываний.
Высказывание, по определению Аристотеля, это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности.
Не всякое языковое образование можно назвать высказыванием. Например, «Высказывание этого предложения является ложным» - парадокс, так как высказывание ссылается само на себя.
Логика высказываний – это ограниченная система (формальный язык), в котором в качестве высказываний допускаются только определенные языковые формы – формулы.
Константные высказывания: истина – TRUE и ложь – FALSE.
Логические операции “не”, “и”, “или” – NOT, AND, OR …

Кодирование информации
Информация….может быть представлена функцией
y = f (x,t),
t – время, х – точка, в которой измеряется некоторое поле, y – значение величины этого поля.
Различают непрерывную информацию и дискретную.
Скалярные величины x,t,y, могут принимать непрерывный ряд значений, описываемых вещественными числами. Непрерывный в том смысле, что значения можно получить в сколь угодно близких точках. Такую информацию называют непрерывной или аналоговой.
Установив какой-то шаг изменения скалярных величин x и t при определении поля y, получают так называемое дискретное представление информации.
Дискретную информацию называют универсальной, т.к. любую непрерывную можно аппроксимировать дискретной с заданной степенью точности.

Дискретную информацию отождествляют с цифровой
Цифровая информация – это частный случай алфавитного представления.
Алфавит, абстрактный алфавит – это конечный набор символов любой природы. Например, десятичные цифры вместе с запятой представляют собой алфавит из 11 символов для представления целых и вещественных чисел. 26 букв латинского алфавита, алфавит русского языка…
В информатике часто приходится представлять символы одного алфавита с помощью символов другого алфавита. Такое преобразование информации называют кодированием.
Проблема кодирования решается просто, если символов кодирующего алфавита больше, чем символов кодируемого, например:
0 – а, 1 – б, 2 – в, 3 – г и т.д.
0 – ноль, 1 – один, 2 – два, 3 – три, и т.д.

Если кодируемый алфавит состоит из большего количества символов, чем кодирующий, то условием правильного, однозначного кодирования является использование последовательностей символов кодирующего для представления одного символа кодируемого алфавита, например,
а – 01, б – 02, в – 03, г – 04 и т.д.
Простейший абстрактный алфавит – это алфавит из двух символов, двух букв, называемый двоичным. В качестве символов алфавита часто используются цифры 0 и 1.
Величина, способная принимать только два значения 0 и 1, является минимальной единицей информации и называется битом. Как самый простой, двоичный алфавит используется в вычислительных машинах, а для кодирования алфавитов, которыми привык пользоваться человек, используются последовательности символов двоичного алфавита.
Последовательностями из n двоичных цифр можно закодировать 2n символов. При n=3 это 23 - 8 символов,
при n = 8 это 28 – 256 символов.

Последовательность из 8 бит - получила название байт, а составленный из различных таких последовательностей 256 символьный алфавит - байтовый алфавит. Его достаточно для кодирования любого существующего в мире алфавита, кроме иероглифов.
Сегодня в информатике принят в качестве стандарта байтовый алфавит ASCII – американский стандартный код для обмена информацией, разработанный американским институтом стандартов ANSI.
В кодах ASCII слово Hello – это 48 65 6C 6C 6F
или в 2-ом виде: 0100 1000 0110 0101 0110 1100 011 1100 1001 1111
UNICODE – кодировка, использующая 16-разрядные последовательности символов двоичного алфавита. Этот алфавит позволяет закодировать 65536 различных символов, и этого достаточно для представления всех широко используемых китайских и японских иероглифов. UNICODE разработан несколькими фирмами - производителями программного и аппаратного обеспечения.

Международная организация по стандартизации ISO разработала 32-разрядный код, позволяющий представлять более 17 миллионов различных символов
Текстовую информацию удобно представлять с помощью байтового алфавита, для записи одного символа используется один байт, но такая кодировка неэффективна для кодирования и обработки числовой информации. Например, для представления двузначного числа потребуется 16 разрядов, 2 байта, а максимальное число, которое можно записать в двух байтах - это 99.
Двоичная система счисления позволяет записывать в двух байтах числа от 0 до 65535.
Современные компьютеры способны обрабатывать не только символьную и числовую информацию, но и позволяют работать с изображениями, аудио и видеоинформацией.
Способы представления графической информации - растровый и векторный. Растровые методы представляют изображение в виде совокупности точек – (пикселей, пэлов).

Для черно-белого изображения каждая точка представляется одним битом со значением 0 или 1 в зависимости от цвета черная она или белая, а все изображение , состоящее из 1280*1024 точки, представляется т. называемой битовой картой размером 1280*1024 бита.
Цветное изображение требует для представления каждой точки 3n бит, где n – количество бит, отводимых для представления интенсивности каждого из 3-х основных цветов : красного, синего и зеленого.
Факсимильные аппараты, цифровые фотоаппараты, видеокамеры, сканеры преобразуют изображения в графические файлы с растровым форматом. Недостаток растрового изображения – сложность его масштабирования. При увеличении размеров появляется зернистость, ступенчатость.
Векторный способ описывает изображение как совокупность прямых и кривых линий. Их форма и расположение в пространстве и на экране описываются соответствующими уравнениями, на основе которых и создается, генерируется изображение. Этот способ используется для описания шрифтов, поддерживаемых принтерами и мониторами.

Количество информации, способы ее определения.
Информация – это фундаментальное понятие, как вещество и энергия, строгое определение дать невозможно, но существуют несколько подходов к определению информации и определению количества информации: содержательный, алфавитный и вероятностный.
По определению Клода Шеннона, информация – это снятая неопределенность, т.е. информативность сообщения характеризуется содержащейся в нем полезной информацией, той ее частью, которая снимает полностью или уменьшает существующую до ее получения неопределенность какого-то события или ситуации.
Величина неопределенности некоторого события - это количество возможных результатов (исходов) данного события. Например, неопределенность погоды на завтра, или бросания монеты. Такой подход называют содержательным.
Содержательный подход – субъективный, у разных людей степень неопределенности об одном и том же предмете различна.

Математик А.Н. Колмогоров предложил определять количество информации, содержащейся в последовательности символов, минимально возможным количеством двоичных знаков, необходимых для кодирования этой последовательности независимо от содержания, представленного этим сообщением.
Это объективный алфавитный подход. Используя для кодирования 2-ый алфавит, и принимая за единицу информации 1 бит, приходим к тому, что содержательный и алфавитный подходы хорошо согласуются, дают одинаковый результат. Более крупные единицы информации: 1 байт,
1 Килобайт – 1024 байт (210) эксабайт
1 Мегабайт – 1024 Килобайта зеттабайт
1 Гигабайт – 1024 Мегабайта йоттабайт
1 Терабайт – 1024 Гигабайта
1 Петабайт – 1024 Терабайта
Чтобы измерить количество информации в сообщении, надо закодировать сообщение с помощью двоичных цифр 0 и 1 наиболее рациональным способом, позволяющим получить самую короткую последовательность. Длина полученной последовательности нулей и единиц является мерой количества информации в битах.

Такой подход приводит к формуле предложенной в 1928 году Р. Хартли для измерения количества информации I = log2N
I – количество информации которое вмещает один символ
N- элементного алфавита равно log2N.
Это утверждение можно сформулировать по другому: количество информации, при выборе одного предмета из N равнозначных предметов, равно log2N. То есть, именно такое количество информации необходимо для устранения неопределенности при выборе из N равнозначных вариантов.
Вероятностный подход в определении количества информации выражается формулой Шеннона (1948г). Пусть некоторое множество состоит из N предметов. При этом интересующий нас предмет является одним из m

Если каждый предмет этого множества считать уникальным, по формуле Хартли его можно угадать за log2N вопросов.
В данном случае, угадав любой из интересующих нас предметов, мы зададим на log2m вопросов меньше, так как не будем определять какой именно экземпляр нам попался. Общее число вопросов при этом будет выражаться формулой:
I = log2N - log2m = log2N/m = log2 1/p
Например, известно, что итоговой оценкой по информатике у половины обучаемых будет «хорошо», у 1/4 - «отлично», у 1/8 – «удовлетворительно», остальные – неуд. Какое количество информации будет получено после того как станет известно какую именно отметку получил обучаемый?
По формуле Шеннона, если отметкой является 4, то
I = log2 1/(1/2) = log2 2 = 1 бит информации, если 5, то
I = log2 1/(1/4) = log2 4 = 2 бита информации, если 3, то I = log2 1/(1/8) = log2 8 = 3 бита информации

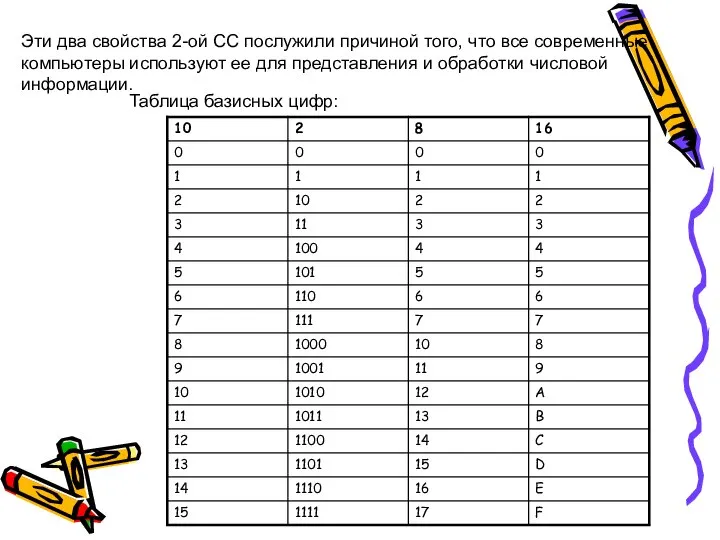
Система счисления (СС)– это совокупность правил записи и наименования чисел.
Существуют позиционные и непозиционные С.С.
СС называется позиционной (непозиционной), если значение цифры числа зависит (не зависит) от местоположения цифры в числе.
Непозиционная СС , например, римская:
I – 1, V - 5, X - 10, L – 50, C - 100, D – 500, M – 1000
XXVII, XLIV
Общепризнанной ПСС является 10-ая СС . Она использует для записи чисел цифры - 0, 1 ,2 ,3, 4. 5, 6, 7, 8, 9.
727,7 = 7 *102+2*101 +7*100 +7*10-1
В позиционной CC число разбивается на разряды слева направо, так что единица старшего разряда в определенное число раз больше единицы соседнего младшего разряда.
Основанием позиционной СС называется количество единиц какого- либо разряда, объединяемых в единицу соседнего старшего разряда.
Основание СС в любой ПСС записывается как 10
Примеры ПСС: 60-ричная, 12-ричная, 5-ричная.

Системы счисления
В ПСС с основанием Р>1 любое число может быть записано
в двух формах: 1) сокращенной и 2) в виде многочлена.
Х = an an-1 an-2 an-3…a1 a0, a-1 a-2 …a-m
Значением числа является сумма значений его цифр.
2) X = an *pn+an-1*pn-1 +an-2*pn-2+….+a1*p1+a0*p0+a-1*p-1+a-2*p-2+…+a-m*p-m
Здесь p – основание СС, 0 =< ai <=P-1 – называют базисными
цифрами данной СС.
Количество базисных цифр равно основанию СС.
В информатике часто используются 2-я, 8-я и 16-я СС.
В двоичной СС наименьшее количество базисных цифр…. Кроме того, в 2-ой СС наиболее простой оказывается арифметика:
Сложение умножение
0 + 0 = 0 0 * 0 = 0
0 + 1 = 1 1 * 0 = 0
1 + 0 = 1 0 * 1 = 0
1 + 1 = 10 1 * 1 = 1

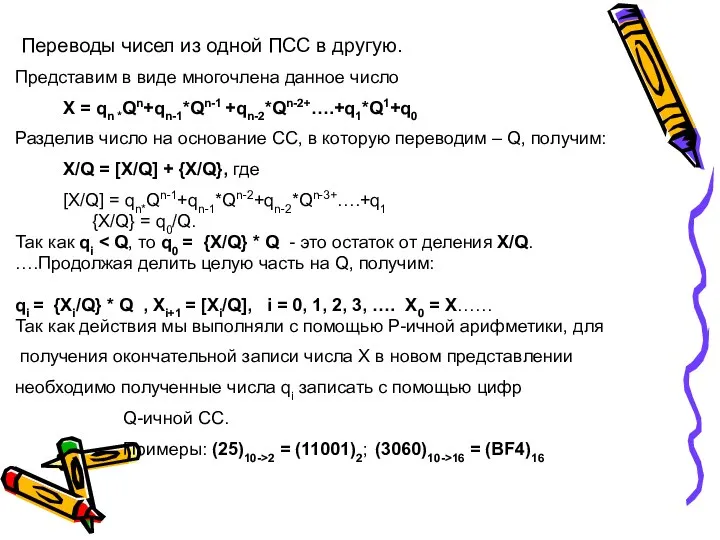
Эти два свойства 2-ой СС послужили причиной того, что все современные компьютеры используют ее для представления и обработки числовой информации.
Таблица базисных цифр:

Переводы чисел из одной ПСС в другую.
Постановка задачи.
Известна запись числа Х в СС с основание P и базисными цифрами 0 <= pi <= P-1, требуется получить запись числа Х в СС с основанием Q и базисными цифрами 0 <= qi <= Q-1.
При рассмотрении правил перевода необходимо помнить правилами арифметики какой СС вы пользуетесь.
«Своя» СС – СС с основание P …
СС с основанием Q - «чужая» СС,…..
Перевод из Q -> P.
Чтобы перевести число из «чужой» СС в «свою», необходимо:
1) представить данное число в виде многочлена;
2) базисные цифры и основание Q-ичной СС записать с помощью P-ичных чисел;
3) выполнить арифметические действия.
Примеры.
1) (125,2)8->10 = 1*102 +2*101 +5*100 + 2*10-1 =
1*82 +2*81 +5*80 +2*8-1 = 64 + 16 + 5 +0,25 = 85,2510

Переводы чисел из одной ПСС в другую. Схема Горнера
2) (101,01)2->10 = 1*102 +0*101 +1*100 + 0*10-1 +1*10-2 =
= 1*22 +0*21 +1*20 +0*2-1 +1*2-2 = 4 + 1 + 0,25 = 5,2510 ;
3). (AB1)16->10 = A*102 +B*101 +1*100 = 10*162 + 11*161 + 1* 160 =
2560 + 176 + 1= 273710.
Для перевода целых чисел из любой системы в 10-ю удобно использовать схему Горнера, согласно которой:
an *pn+an-1*pn-1+an-2*pn-2+….+a1*p1+a0*p0 =
= ((…(an *P + an-1)*P + an-2)*P +….+a1)*P + a0
Например.
13218->10 = ((1*8 + 3)* 8 + 2)* 8 +1 = 72110
12348->10 = ((1*8 + 2)*8 + 3)*8 + 4 = 66810
Перевод из P в Q.
Перевод целых чисел.
Дано Х = (an an-1an-2….a1a0)p,
требуется получить - Х = (qn qn-1qn-2….q1q0)Q

Переводы чисел из одной ПСС в другую.
Представим в виде многочлена данное число
Х = qn *Qn+qn-1*Qn-1 +qn-2*Qn-2+….+q1*Q1+q0
Разделив число на основание СС, в которую переводим – Q, получим:
Х/Q = [X/Q] + {X/Q}, где
[X/Q] = qn*Qn-1+qn-1*Qn-2+qn-2*Qn-3+….+q1
{X/Q} = q0/Q.
Так как qi < Q, то q0 = {X/Q} * Q - это остаток от деления Х/Q.
….Продолжая делить целую часть на Q, получим:
qi = {Xi/Q} * Q , Xi+1 = [Xi/Q], i = 0, 1, 2, 3, …. X0 = X……
Так как действия мы выполняли с помощью P-ичной арифметики, для
получения окончательной записи числа Х в новом представлении
необходимо полученные числа qi записать с помощью цифр
Q-ичной СС.
Примеры: (25)10->2 = (11001)2; (3060)10->16 = (BF4)16

Переводы чисел из одной ПСС в другую.
Перевод дробных чисел.
Дано Х = (0.a-1a-2….a-m)p, требуется получить Х = ( 0.q-1q-2….q-m)Q
Представим в виде многочлена
X = q-1*Q-1+q-2*Q-2+….+q-m*Q-m и умножим на Q
X*Q = [X*Q] + {X*Q}, [X*Q] = q-1
Продолжая умножать дробную часть на Q, получим qi - цифры числа X в новом представлении,... Умножаем до тех пор пока дробная часть станет равной нулю, или мы получим число с заданной степенью точности. Для окончательной записи числа необходимо полученные числа qi записать с помощью цифр Q-ичной CC.
Примеры.
0.810->16 = 0.CCC… 0.810->2 = 0.11001 0.310 ->16 = 0.4СС16

Переводы чисел из одной ПСС в другую.
3. Перевод произвольных чисел.
Для перевода произвольных чисел из P-ичной системы в
Q-ичную достаточно отдельно перевести целую часть и дробную часть и результаты приписать. (3060,8)10->16 = (BF4,C)16
Смешанные СС.
Смешанная Q-P-ичная СС – это СС, в которой каждая цифра P-ичного числа записывается с помощью n Q-ичных цифр, где n – это количество Q-ичных цифр, достаточных для хранения старшей Р-ичной цифры.
Например, число 2410 в 2-10-й СС равно 0010 01002-10.
Переводы чисел для СС, связанных соотношением P = Qn.
1). Перевод из P в Q. Чтобы перевести число из СС с основанием P в СС с основанием Q, достаточно каждую цифру данного числа записать с помощью n Q-ичных разрядов, используя таблицу представления базисных цифр.

Переводы чисел для СС, связанных соотношением P = Qn.
Числа с фиксированной и плавающей точкой.
2). Перевод из Q в P. Чтобы перевести число из СС с основанием Q в СС с основанием P, достаточно данное число разбить влево и вправо от запятой на группы по n разрядов, неполные крайние группы можно дополнить нулями. Затем каждую такую группу записать с помощью одной P-ичной цифры.
Примеры.
(1BF9,51)16->2->8 = 0001 1011 1111 1001, 0101 00012 = 15771,2428
(7541,23)8-2-16 = 111 101 100 001,010 0112 = F61,4C16
Числа с фиксированной и плавающей точкой.
X = знак(anan-1an-2…a0.a-1a-2…..a-m)p - это запись числа с
фиксированной точкой.
Записываем в виде многочлена:
Х = знак(an*Pn + an-1*Pn-1+an-2*Pn-2+…+a0*P0+a-1*P-1+a-2*P-2+…+a-mP-m)P
Вынесем за скобку в качестве множителя Pk и свернем, получим число в форме с плавающей точкой.

Числа с фиксированной и плавающей точкой. Нормализованные числа.
Х = знак(an*Pn-k + an-1*Pn-1-k+an-2*Pn-2-k+.. …+a0*P-k+ak-1*P-1+ak-2*P-2+…
+a-mP-m-k)*Pk
1) X = знак(anan-1an-2…ak,ak-1ak-2…..a-m)*Pk или
2) X = знак |M| * Pзнак |n|
Число с плавающей точкой называется нормализованным числом, если
в записи 1) k = n+1 и an <> 0, или
в записи 2) мантисса M удовлетворяет условию 1/P <= |M| < 1.
Например: 3.1415926 0.0031415926*103
314.15926*10-2 0.31415926*101

Арифметические действия над числами с плавающей точкой
M1*2p1 + M2 *2p2 = M*2p ,
если P1 > P2, то вычисляется P1 – P2 , M2 сдвигается на
(P1 – P2 ) разрядов вправо, мантиссы складываются, результат нормализуется, так что порядок суммы чисел
P = P1 + P/ ,
где P/ учет нормализации мантиссы результата суммирования.
2. Вычитание сводится к сложению
3. Умножение: M = M1 * M2 и P = P1 + P2 + P/
4. Деление: M = M1 / M2 и P = P1 - P2 + P/

Нетрадиционные позиционные системы счисления..
ПСС делят на традиционные, нетрадиционные и смешанные.
Все ПСС одинаковы в том смысле, что:
Арифметические операции выполняются по одним и тем же правилам;
Справедливы одни и те же законы арифметики ….
Правила выполнения арифметических действий опираются на таблицы сложения и умножения в P-ичной СС.
Для традиционных ПСС вводится понятие базис и основание СС так, что базис – это последовательность чисел, каждое из которых задает значение цифры по ее месту в записи, т.е. задает вес каждого разряда.
Базис 10-ой СС – это 1, 101, 102, 103 , 104….10n
В общем виде: ….P-2, p-1, 1, p, p2 p3….pn
Знаменатель P геометрической прогрессии, члены которой образуют базис традиционной СС, является основанием СС.

Нетрадиционные позиционные системы счисления. Факториальная ПСС
В традиционных ПСС вес единиц разрядов числа растет справа налево равномерно в P раз, где P – основание СС. В нетрадиционных ПСС вес единиц разрядов в числе также растет, но не равномерно, а по какому-либо другому закону.
Например, число, записанное в факториальной ПСС имеет значение в 10-ой СС, равное сумме факториалов n первых натуральных чисел, умноженных на цифры факториальной записи числа.
3221ф = 3 * 4! + 2 * 3! + 2 * 2! + 1* 1! = 8910
40301ф = 4*5! + 3*3! + 1*1! = 49910
Чтобы перевести число из 10-ой СС в факториальную, необходимо разделить данное число на 2, затем целую часть разделить на 3, затем на 4 и т. д. пока целая часть не окажется равной нулю.
Для нетрадиционных ПСС не используется понятие основание СС, а используется понятие ,базис и базисные цифры. А базисные цифры – это символы алфавита этой СС, этого формального языка.

Нетрадиционные позиционные системы счисления. Фибоначчиева ПСС. Уравновешенные СС.
Фибоначчиева ПСС в качестве базиса использует числа ряда Фибоначчи (1,2,3,5,8,13,21,34,55,….), а символами алфавита являются 0 и 1. Тогда число в фибоначчиевой СС может быть записано так:
3710 = 34 + 3 = 10000100фиб = 1*34 + 0*21 + 0*13 +0*8 + 0*5 +1*3+ 0*2 +0*1;
2510 = 21 + 3 +1 = 1000101фиб
Нетрадиционные ПСС используются для кодирования чисел, их особенности и области применения – это предмет исследования.
Уравновешенная, например, троичная СС имеет алфавит -1, 0, 1.
Пример. -11-1013 = -1*34 + 1*33 -1*32 +0*31 +1*30 = 6210
Главная особенность уравновешенных СС – для представления в компьютере не нужно выделять разряд для знака и при выполнении арифметических операций не используется правило знаков.

Нетрадиционные позиционные системы счисления. Фибоначчиева ПСС. Уравновешенные СС.
В 1959 году была построена ЭВМ Сетунь, работавшая на 3-ой уравновешенной арифметике. В 1962 – 1965 годах было 50 промышленных экземпляров, превосходивших по быстродействию ЭВМ такого же класса и более дешевые.
Создали Сетунь в МГУ С.Л. Соболев, Н.П. Брусенцов, С.П. Маслов.
В ЭВМ ENIAK использовалась двоично-пятиричная СС, в которой каждая цифра 10-ой СС заменялась двумя цифрами: одна – это 0 или 5, а вторая – это 0,1,2,3, или 4 так, чтобы в сумме получалась требуемая цифра.

Формализованные понятия алгоритма
Алгоритмы являются необходимым этапом при автоматизации решения задач, средством описания сложных процессов, формой изложения научных результатов, средством, позволяющим экономить умственный труд, и даже одним из средств обоснования математики.
Алгоритмы могут быть разработаны на основе наблюдения и эксперимента, их называют имитационными и эмпирическими. Алгоритмы могут быть выведены, исходя из научных положений и теорем, с помощью конструирования из уже имеющихся, Как бы не был разработан алгоритм, он должен быть обоснован, должна быть доказана его корректность и для этого используются как теоретические, так и экспериментальные методы.
Интуитивное понятие: алгоритм – это правило, сформулированное на некотором языке и определяющее последовательность действий, преобразующих допустимые исходные данные в искомые результаты.

Формализованные понятия алгоритма
Последовательность действий, состоящая из четких, понятных, однозначно определенных шагов, называют алгоритмическим процессом. Основные свойства: массовость, детерминированность и результативность…..
Понятность алгоритмического процесса истолковывается как наличие некоторого алгоритма, определяющего процесс выполнения алгоритма решения какой-либо задачи, т.е. наличие исполнителя, который знает правила выполнения других алгоритмов. А исполнителем может быть как человек, так и машина. Интуитивность этого определения алгоритма заключается в том, что не ясен научный смысл таких слов, как понятность, четкость.
Существует большое количество математических алгоритмов…….в 9 веке Узбекский математик Ал-Хорезми….,алгоритм Евклида (НОД), решето Эратосфена (поиск простых чисел), определение НОК, правила дифференцирования и интегрирования, решение систем уравнений и т.д.

Формализованные понятия алгоритма.
Но в математике существуют и такие задачи, для которых не могут быть построены алгоритмы их решения….Существование алгоритмически неразрешимых задач было одной из причин, побудивших математиков заняться теорией алгоритмов. Второй причиной стала необходимость обоснования математики, возникшая в связи с кризисом в математике, который не смогла преодолеть и теория множеств, разработанная немецким математиком Г. Кантором в 1874-1897гг.
Парадоксы, обнаруженные в теории множеств, привели к тому, что в математике появилось направление, получившее название конструктивного. Математики – конструктивисты считают, что исходным материалом для математических построений могут служить лишь наиболее простые математические объекты, применение которых оправдано всей практикой человечества. Количество их ограничено, а в качестве основного средства получения новых математических объектов должны служить алгоритмы.

Формализованные понятия алгоритма. Рекурсивные функции.
Благодаря математикам-конструктивистам существуют формализованные понятия алгоритма. Они связаны с понятиями рекурсивных функций, машин Тьюринга, нормальных алгоритмов Маркова.
Рекурсивные функции. Факт существования или не существования алгоритма можно установить, если найти такой математический объект, который существует в точности тогда, когда и алгоритм. Таким объектом может быть, например, рекурсивная функция.
Функция в математике определяется однозначно y = f(x1,x2,…xn), если существует закон, по которому каждому набору значений аргументов x1,x2,…xn ставится в соответствие одно значение y. Закон может быть произвольным, им может быть алгоритм, определяющий способ получения значения функции, такую функцию называют вычислимой. Рекурсивные функции – это частный класс вычислимых функций, а алгоритмы, являющиеся законами их определения, называются алгоритмами, сопутствующими рекурсивным функциям.

Рекурсивные функции
Здесь рекурсивные функции определены на множестве целых неотрицательных чисел.
Выделяются три базовые, наиболее простые функции, для которых сопутствующие алгоритмы являются простыми, одношаговыми, не вызывающими сомнений. Затем используются три приема, называемые операторами подстановки, рекурсии и минимизации, с помощью которых из уже существующих рекурсивных функций, можно получить новые функции. Эти операторы, по существу являются алгоритмами, соединяя которые, можно получать новые алгоритмы, сопутствующие рекурсивным функциям.
Базовые рекурсивные функции: 1) Функция любого числа переменных, равная нулю.
y = φ1(x), w = φ3(x,y,z),
например, φ1(5) = 0, φ3(2,5,7) = 0 и т.д. φ () = φ0 .
Сопутствующий алгоритм: если знак функции имеет вид φn , то любой совокупности значений аргументов данной функции ставится в соответствие значение ноль.

Рекурсивные функции
2) Тождественные функции n независимых аргументов вида ψn,i
где n є N, 1=< i <=n, n – количество аргументов, i = номер одного
из них. w = ψ3,2 (x,y,z), w = ψ3,2 (2,8,5) = 8.
Сопутствующий алгоритм: если знак функции имеет вид ψn,i , то значением ее считать значение i-го аргумента, считая слева направо.
3) Функция следования, (получения последователя), одного аргумента, функциональный знак λ.
Сопутствующий алгоритм: если знак функции λ, то значением ее считать число, непосредственно следующее за значением аргумента. Обозначают λ(x) = x/, λ(5) = 6, 5/ = 6.
Операторы подстановки, рекурсии и минимизации.
1) Оператор подстановки (суперпозиции). Φ = F( f1,f2,f3,…fn).
Сопутствующий алгоритм: значения функций f1,f2,f3,…fn принять за аргументы и вычислить значение функции F. Например,
i (y) = λ(λ(y)) = λ(y)/) = y//
i (5) = λ(λ(5)) = λ(6) = 7.

Рекурсивные функции
Оператор подстановки обозначают буквой S и записывают построение функции Φ из F и fi так:
Φ ::= S [ F; f1,f2,….fn ] , например, i (y) ::= S [ λ(x); (λ(y))]
2) Оператор рекурсии обозначают буквой R и его применение записывается в виде:
f ::= R [f1,f2; x, (y)], где
f - определяемая функция, зависящая от n аргументов, функция, которую мы строим. f1 – функция n-1 независимой переменной,
f2 – функция n+1 независимой переменной, из них n -1 совпадают с параметрами функции f1, еще два – это дополнительные аргументы x и y. x – называют главным, он войдет в определяемую функцию, а y – вспомогательным, он используется при выполнении оператора рекурсии.
Оператор рекурсии задает функцию с помощью двух условий, в которые входят f1 и f2 :
f (0) = f1, f(i/) = f2 (i, f(i))

Рекурсивные функции
Алгоритм, сопутствующий рекурсивной функции:
Значением получаемой функции для нулевого значения главного дополнительного аргумента считать значение функции f1 – (первое условие), а для каждого последующего значения главного дополнительного аргумента считать значение второй функции f2 при предыдущем значении главного аргумента и при значении вспомогательного, совпадающего с предыдущим значением определяемой функции f (второе условие).
Например, построим функцию предыдущее от x, обозначив ее pr(x), с помощью функции рекурсии так:
pr(x) ::= R [φ0, ψ2,1 (x,y) ; x, (y) ],
где φ0, ψ2,1 - базовые рекурсивные функции. Эта функция определяется условиями: pr(0) = φ0 и pr(i/) = ψ2,1 (i, pr(i)), т.е.
pr(0) = φ0 = 0, pr(1) = ψ2,1 (0, pr(0)) = 0, pr(2) = ψ2,1 (1, pr(1)) = 1, и т.д.
Здесь pr(0) = 0, а не 1, так как рекурсивные функции определены на множестве целых неотрицательных функций.

Рекурсивные функции
Оператор минимизации называется оператором построения по первому нулю. Знак функции µ, применение этого оператора:
f ::= μ [f1 ;(x)] , где x – вспомогательный, исчезающий аргумент. Оператор минимизации по заданной функции n+1 аргумента строит функцию n аргументов.
Сопутствующий алгоритм: придавать вспомогательному аргументу последовательные значения, начиная с нуля до тех пор, пока не окажется, что f1 = 0, тогда это значение вспомогательного аргумента принять за значение определяемой функции f для тех главных аргументов, для которых выполнялись вычисления.
Базовые функции и все, построенные без использования оператора минимизации, определены для всех значений аргументов, но функции, построенные с помощью этого оператора могут быть не определены, т.к. исходная функция f1 может не обращаться в ноль ни при каких значениях.

Рекурсивные функции
Рекурсивные функции, которые определены не для всех возможных аргументов, называются частично-рекурсивными.
Рекурсивные функции, построенные без использования оператора минимизации, называются примитивно рекурсивными.
Рекурсивные функции, определенные на всех значениях аргументов называются общерекурсивными.
Оказывается, что многие известные математические функции являются рекурсивными: y = x +1 совпадает с базовой функцией λ(x) и следовательно рекурсивна.
Доказательство того, что функция w = x + y является рекурсивной, может быть получено, если с помощью подстановки функции
z + 1 вместо z в функцию ψ3,3(x,y,z), получим функцию
f*(x,y,z) = z + 1, а затем с помощью рекурсии получим
S(x,0) = ψ1,1(x) = x; S(x,1) = S(x,0) + 1 = x +1;
S(x,2) = S(x,1) + 1 = x +2;
и т.д. S(x,y) = x +y
(значение S на предыдущем шаге z + 1).

Рекурсивные функции
Американский ученый А. Черч высказал предположение, что понятием рекурсивной функции исчерпывается понятие вычислимой функции.
Основной тезис Черча: каков бы не был алгоритм, перерабатывающий наборы целых неотрицательных чисел в целые неотрицательные числа, существует алгоритм, сопутствующий рекурсивной функции, который ему эквивалентен.
Т.е. вычисление функции эквивалентно вычислению сопутствующего алгоритма. И так как для каждого алгоритма должна существовать рекурсивная функция, то если невозможно построить рекурсивную функцию, то невозможно разработать алгоритм решения данной задачи.

Машина Тьюринга.
Другой подход к уточнению понятия алгоритм предложил английский математик А. Тьюринг. Он обратил внимание на исполнителя алгоритмов и описал в 1937 году воображаемую машину (без ограничения на ее ресурсы, перерабатывающую исходную последовательность символов в последовательность символов результирующую.
Основной частью этой машины, определяющей действия исполнителя, является функциональная таблица, которая описывает процесс преобразования исходного данного. Машина Тьюринга – это не машина, не механизмы, а некоторые тексты на естественном языке, описывающие устройства и выполняемые ими действия. Так что можно считать машину Тьюринга алгоритмом, записью которого является функциональная таблица, а правилом, алгоритмом его выполнения - описание действия устройства этой машины.
Устанавливаемое машиной Тьюринга соответствие между исходными данными и результатами ее работы представляет собой в математическом смысле некоторую функцию.

Машина Тьюринга.
Тезис Тьюринга: любая вычислимая функция – вычислима по Тьюрингу, т.е. для нее может быть построена машина Тьюринга, может быть построен алгоритм. И для вычисления рекурсивных функций может быть построена машина Тьюринга. Используя кодирование, можно установить соответствие между преобразованиями слов, осуществляемыми машиной Тьюринга, и некоторыми целочисленными неотрицательными функциями.
Еще один подход предложил советский ученый А. Марков, использующий в качестве исходных данных и результатов последовательности букв, слова.
Доказано, что в теоретическом плане эти теории эквивалентны – результаты, полученные с помощью одной, могут быть получены с помощью другой. Однако они охватывают узкий класс алгоритмов и пригодны для решения теоретических вопросов.

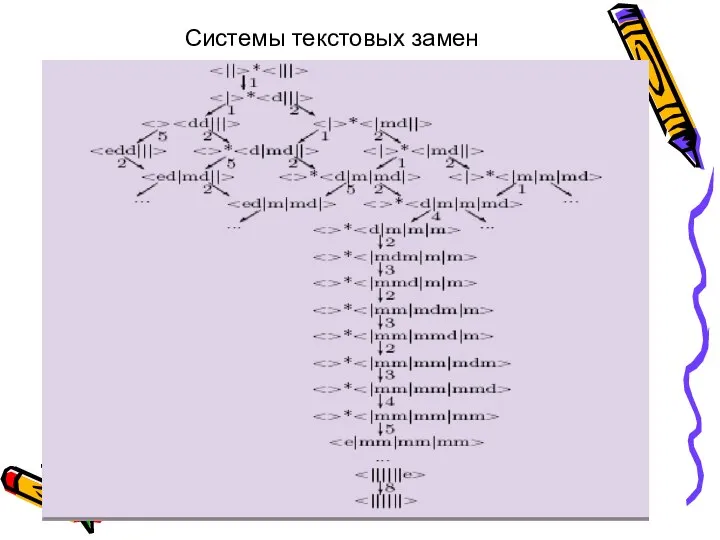
Нормальные алгоритмы Маркова. Системы текстовых замен (СТЗ)
Алгоритмы бывают последовательными и параллельными, разветвляющимися и циклическими, рекурсивными.
Алгоритм называется терминистическим, если он для всех последовательностей шагов обработки информации заканчивается после конечного числа шагов.
Алгоритм называется детерминистическим, если нет никакой свободы в выборе очередного шага обработки.
Алгоритм называется детерминированным, если результат его определен однозначно.
Пусть алгоритм на входе и выходе использует слова из множества V* над некоторым набором символов V. Любую информацию можно представить в виде слов. Простейшими шагами обработки слов являются замена определенных подслов-образцов другими словами. Такой подход приводит к записи алгоритмов в форме СТЗ.
СТЗ – это конечное множество замен R над множеством символов V є V*.

Нормальные алгоритмы Маркова.
Пусть V – множество символов. Пара ( v, w) є V * X V* называется заменой над V. Часто замену записывают в виде v w.
Конечное множество замен R будем называть системой текстовых замен (СТЗ) над V.
Элементы этой системы называют правилами текстовых замен - ПТЗ
СТЗ служат для представления алгоритмов. Отдельные шаги этих алгоритмов это применение правил замен.
Замена s t называется применением правила v w, если имеются слова a, v, w, z є V * такие, что справедливо:
s = a 0 v 0 z, t = a 0 w 0 z

Системы текстовых замен

Системы текстовых замен

Системы текстовых замен

Системы текстовых замен

Системы текстовых замен

Системы текстовых замен

Системы текстовых замен

Нормальные алгоритмы Маркова.
Для входного слова < I…I > x < I….I > с n1 штрихами в первом операнде и n2 во втором операнде алгоритм дает выходное слово с n1 x n2.
В общем случае АТЗ недетерминистические и недетерминированные. Для входа t могут существовать различные вычисления, с различными результатами. Например, если СТЗ содержит правила: аа в и а аа, то любое слово t, содержащее символ а, будет нетерминальным и если будем применять 2-е правило только тогда, когда неприменимо 1-е, то вычисление будет завершающимся, если применять только 2-е правило, то не завершающимся, а при произвольном применении правил, можно получить различные результаты для одного и того же входного слова.
Нормальные алгоритмы Маркова детерминистические и детерминированные. Детерминизм достигается за счет установления приоритетов применения правил замен. Марковская стратегия: 1) – если применимы 2 правила….,
2) – если одно правило применимо в двух местах….

Системы текстовых замен

Системы текстовых замен

Системы текстовых замен

Способы описания языков программирования
Для описания языков программирования используются Бэкуса-Наура форма, БНФ-нотация и синтаксические диаграммы.
1958 год – описание ЯПр Паскаль.
Естественные языки для описания формальных языков неприемлемы….
Описываемый формальный язык – это язык-объект, а описывающий ФЯ – это метаязык.
Метасинтаксические языки и метасемантические языки…
БНФ-нотация – это метасинтаксический язык для описания ЯПр. Однако существуют сложные дополнительные условия правильного формирования программ, называемые контекстными условиями, которые формулируются с помощью специальных предикатов.
Значения отдельных элементов языка определяют семантику языка.

Синтаксис ЯПр устанавливается над множеством основных символов С, которые могут использоваться для записи программ. Над этими символами выделяется подмножество последовательностей символов S Є C* как язык. Синтаксис описывает множество последовательностей символов, которые внешне представляют правильно сформулированные программы.
БНФ-нотация позволяет записать эти последовательности символов как некоторые выражения, в силу простоты построения их называют регулярными выражениями.
Символы множества С называют терминальными.
Регулярные выражения над множеством С определяют формальный язык.

Отдельные элементы регулярных выражений и их значения:
1.Терминальные символы. Пусть с Є С, тогда говорят,
что с – есть регулярное выражение с языком {
}
2. Объединение. Пусть R и Q – РВ с языками X и Y, тогда
R | Q - обозначает РВ с языком X U Y
3. Конкатенация. Пусть R и Q с языками X и Y, тогда RQ обозначает РВ с языком {x 0 y: x Є X, y Є Y }
4. Обозначения: пусть R – это РВ с языком X, тогда
{R} – РВ с языком X U { ε };
{ R }* - РВ с языком { x1 0 x2 0……0 xn: n Є N λ x1, x2, …xn Є X }
{ R }+ - РВ с языком {x1 0 x2 0……0 xn : n Є N λ n > 0 λ x1, x2, …xn Є X }
[ R ] – РВ с языком X
{ } – РВ с языком Ø
Формулы БНФ-нотации записываются в виде < e > ::= R
::= - метасимвол «по определению есть», I – или, а < ….> - нетерминальные символы.

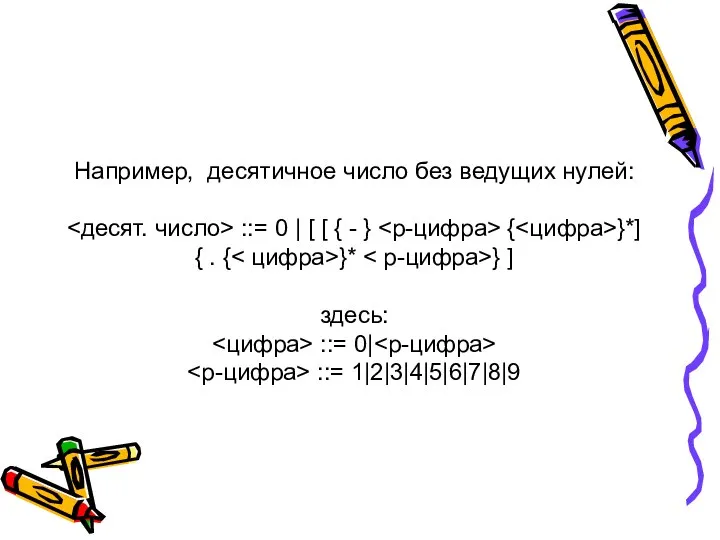
Например, десятичное число без ведущих нулей:
<десят. число> ::= 0 | [ [ { - } <р-цифра> {<цифра>}*]
{ . {< цифра>}* < р-цифра>} ]
здесь:
<цифра> ::= 0|<р-цифра>
<р-цифра> ::= 1|2|3|4|5|6|7|8|9

БНФ- нотация
::= R называется рекурсивной, если
входит в R. Рекурсивные БНФ-нотации позволяют описывать формальные языки, для описания которых недостаточно только регулярных выражений, например, формальные языки, содержащие вложенные структуры.
Например, арифм-ое выр-ие в БНФ-нотации на множестве символов {0,1,,…9,(,),+,-,*,/} определяется следующим образом:
<арифм. выр-ие> ::= <число>I<(арифм. выр-ие)>I
арифм. выр-ие> {+ I – I * I /}+ <арифм. выр-ие>
<число> ::= [<цифра> {<цифра>I0}*]I0
<цифра> ::= 0I1I2I3I4I5I6I7I8I9
Здесь число определено так, что последовательности цифр с ведущими нулями не допускаются.
<идентификатор> ::= <буква>I<идентификатор> <буква>I <идентификатор> <цифра>