Содержание
- 2. СЖАТИЕ Сжатие данных Кодирование по алгоритму Хаффмана Межсимвольная зависимость Избыточность в английском языке Кодирование Лемпеля –
- 3. Сжатие данных (data compression) – процедура уменьшения их объёма с сохранением (полным или частичным) их целостности.
- 5. Способы решения (устранения избыточности): 1. Замена часто встречающихся данных короткими кодовыми словами, а редких – длинными
- 6. Сжатие данных, не обладающих свойством избыточности (например, случайный сигнал или белый шум, зашифрованные сообщения), принципиально невозможно
- 7. Все методы сжатия данных делятся на два основных класса: Сжатие без потерь (полное восстановление исходных данных)
- 8. два способа сжатия текста (сжатие без потерь): Кодирование Хаффмана (энтропийное кодирование) Кодирование Лемпеля-Зива (LZ77)
- 9. Алгоритм Хаффмана – это один из первых методов, в основе которого лежит энтропийное кодирование (кодирование источника).
- 11. АЛГОРИТМ ХАФФМАНА Алгоритм состоит из двух этапов: 1. Сначала символы источника сокращаются путем последовательного образования сложных
- 12. Рассмотрим источник из пяти символов с заданными вероятностями. ПРИМЕР 1
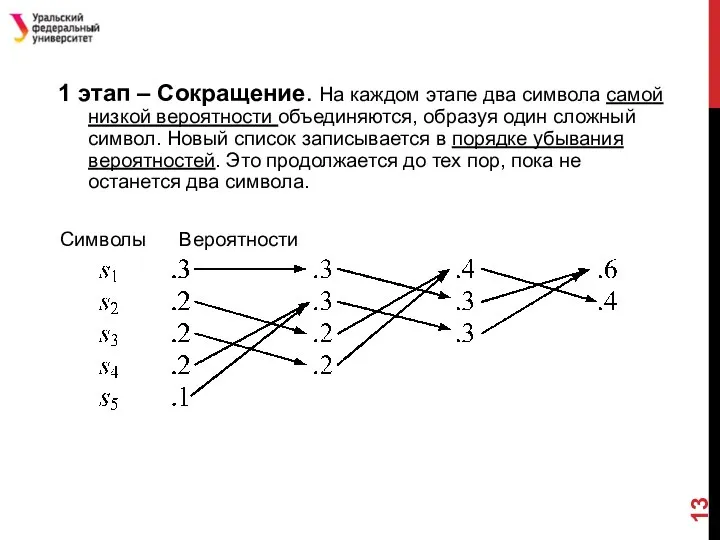
- 13. 1 этап – Сокращение. На каждом этапе два символа самой низкой вероятности объединяются, образуя один сложный
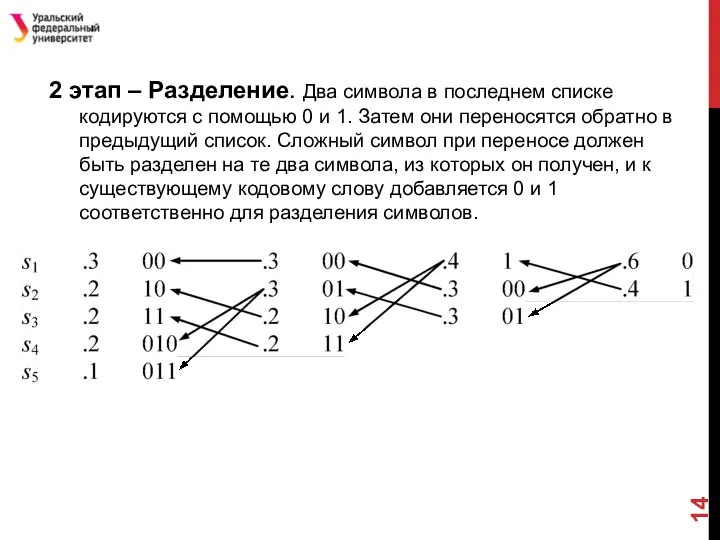
- 14. 2 этап – Разделение. Два символа в последнем списке кодируются с помощью 0 и 1. Затем
- 15. Итак, мы получили код: Символ источника Вероятность Код s1 0.3 00 s2 0.2 10 s3 0.2
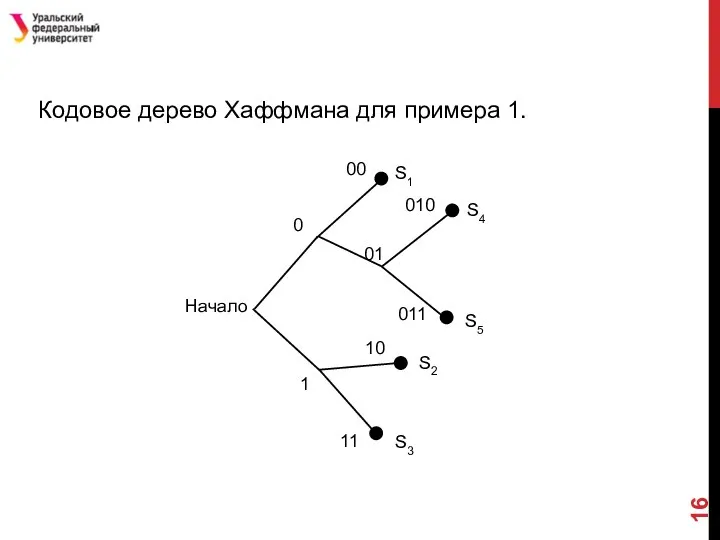
- 16. Кодовое дерево Хаффмана для примера 1.
- 17. Неоднозначность кодов Хаффмана. Попробуйте построить два различных кода Хаффмана для пятисимвольного источника. ПРИМЕР 2
- 18. Результат: два кода построены по методике Хаффмана и имеют одинаковую среднюю длину.
- 19. ПРИМЕР 3
- 21. Межсимвольная зависимость. Следующие друг за другом символы от источника не всегда являются независимыми. Наоборот, текущие вероятности
- 22. ВЕРОЯТНОСТИ В АНГЛИЙСКОМ ЯЗЫКЕ
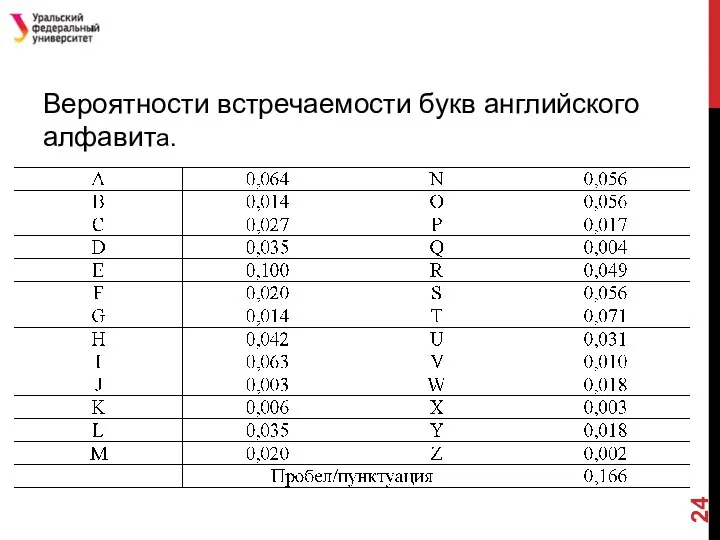
- 24. Вероятности встречаемости букв английского алфавита.
- 26. Таким образом, код Хаффмана для алфавита будет иметь среднюю длину ближе к четырем, чем к пяти.
- 27. ПРИМЕНЕНИЕ ЗАКОНОВ ЦИПФА (ЗИПФА)
- 28. Для расчета Шеннон воспользовался законом Ципфа. (Джордж Ципф в 1949 г. эмпирически вывел соотношение частотностей слов).
- 31. ИЗБЫТОЧНОСТЬ АНГЛИЙСКОГО ЯЗЫКА
- 33. Выводы: Имеется огромная возможность для компрессии английского текста. Текстовый файл может теоретически быть спрессован до размера,
- 34. КОДИРОВАНИЕ ЛЕМПЕЛЯ – ЗИВА Новаторский и талантливый метод компрессии предложили Зив и Лемпель в 1977 г.
- 35. В методе Лемпеля – Зива и отправитель, и получатель ведут запись того, что уже было отправлено.
- 37. ПРИМЕР. LZ77 Исходный текст: THIS-THESIS-IS-THE-THESIS. Передаваемые сообщения (код LZ77): (0, 0, T) T (0, 0, H)
- 38. Задания: 1) Закодируйте сообщение: ROCCOBAROCCO. Код LZ77: (0,0,’R’) (0,0,’O’) (0,0,’C’) (1,1,’O’) (0,0,’B’) (0,0,’A’) (7,5,’.’) 2) Декодируйте
- 39. СОВРЕМЕННЫЕ АРХИВАТОРЫ
- 40. ДРУГИЕ ФОРМЫ СЖАТИЯ ИНФОРМАЦИИ Кроме текста, сжатие также применяется к графике, изображениям, речи, видео…(эти данные не
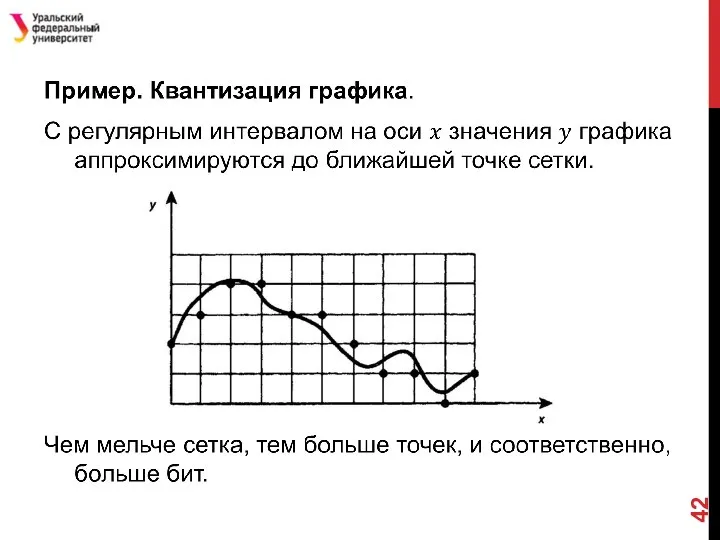
- 41. Общепринятой является обработка этих видов данных первоначально посредством дискретизации временного и пространственного измерения, а также уровней
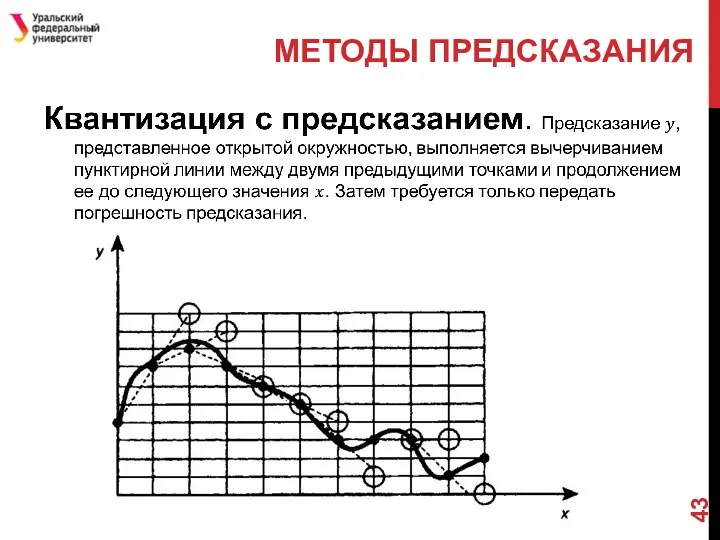
- 43. МЕТОДЫ ПРЕДСКАЗАНИЯ
- 45. JPEG Стандарты сжатия графической информации были установлены комитетом, который называется Совместной группой экспертов по фотографии (Joint
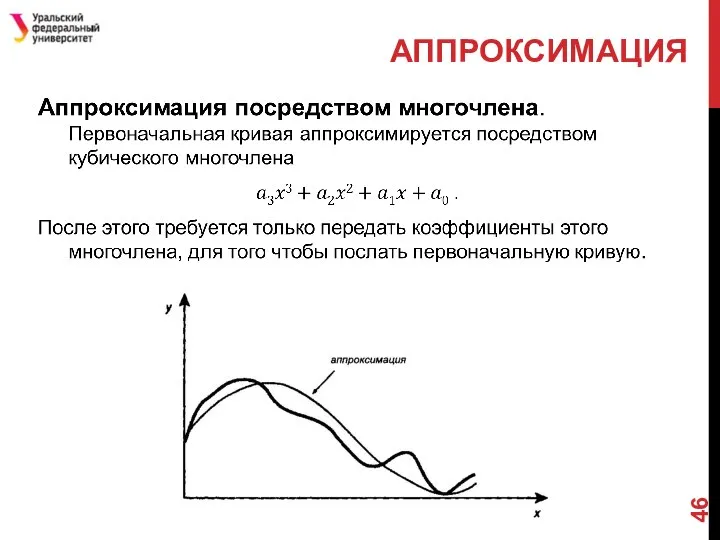
- 46. АППРОКСИМАЦИЯ
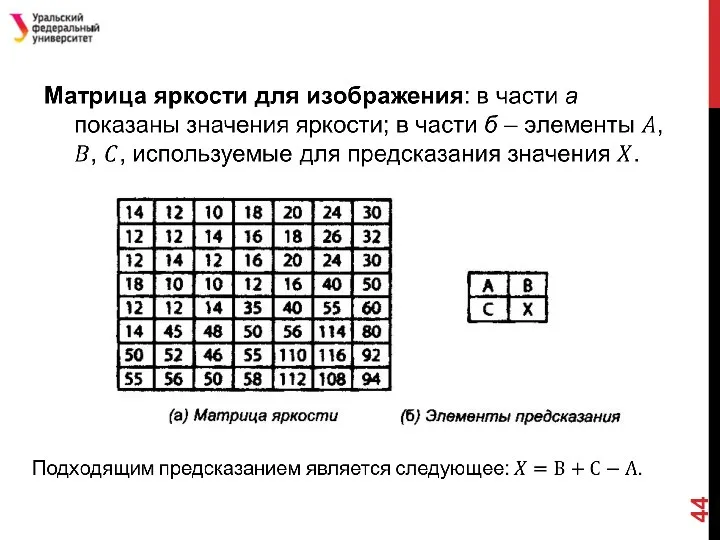
- 47. Популярная версия JPEG аппроксимирует матрицу яркости посредством серии двухмерных функций косинуса и записывает коэффициенты этой серии.
- 48. МРЗ MPEG (филиал комитета JPEG) – группа экспертов по киноизображениям разработала стандарты сжатия для киноизображений и
- 49. Упражнения 1. (Шестисимвольный источник.) Источник имеет шесть символов с нижеуказанными вероятностями. s1 0,3 s4 0,1 s2
- 50. 2. (Пятисимвольный источник.) Найти три различных кода Хаффмана для источника. s1 0,4 s4 0,1 s2 0,2
- 51. 3. (Преимущество алгоритма Хаффмана.) Преимущество компрессии при кодировании по алгоритму Хаффмана S2 вместо S является наиболее
- 52. 4. (Вычитание Хаффмена.) Рассмотрите источник со связанными с ним символами и вероятностями Один код Хаффмена для
- 53. 5. (Пример LZ77.) Декодируйте сообщение (0, 0, ‘a’) (0, 0, ‘b’) (0, 0, ‘r’) (3, 1,
- 55. Скачать презентацию












































 Автоматизация подписок и лайков. Массфолловинг
Автоматизация подписок и лайков. Массфолловинг ”Ватник” контент-анализ метафоры в медиасреде
”Ватник” контент-анализ метафоры в медиасреде Codecraft HTML
Codecraft HTML Инструкция по получению электроной почты студента
Инструкция по получению электроной почты студента Фото/история персонажа из игры Warcraft III
Фото/история персонажа из игры Warcraft III Программное обеспечение компьютерных сетей
Программное обеспечение компьютерных сетей Обобщенная модель нейрона. Персептрон (структура, алгоритмы обучения). Решение задачи распознавания образов с помощью НС
Обобщенная модель нейрона. Персептрон (структура, алгоритмы обучения). Решение задачи распознавания образов с помощью НС Линейные алгоритмы
Линейные алгоритмы Разрешения на доступ к этой презентации
Разрешения на доступ к этой презентации 3S System of Secure Stream. Возможности программы распознавания лиц 3S. Возможности и особенности настройки
3S System of Secure Stream. Возможности программы распознавания лиц 3S. Возможности и особенности настройки Разработка программных средств анализа информационного контента для формирования запросов к поисковым системам
Разработка программных средств анализа информационного контента для формирования запросов к поисковым системам Стандарт электронно-цифровой подписи ГОСТ Р 34.10 различия версий 94 и 12 годов
Стандарт электронно-цифровой подписи ГОСТ Р 34.10 различия версий 94 и 12 годов DIXI CENTER. Разработка многофункциональных B2B2C систем
DIXI CENTER. Разработка многофункциональных B2B2C систем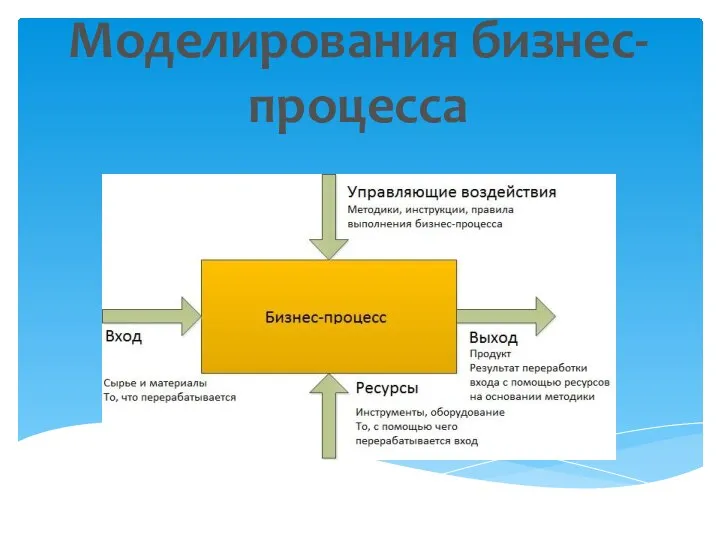 Моделирования бизнес-процесса
Моделирования бизнес-процесса Электрнонный рекомендательный список. Разработка
Электрнонный рекомендательный список. Разработка Требования к презентации
Требования к презентации Обзор бесплатных онлайнсервисов в сети интернет и их возможности
Обзор бесплатных онлайнсервисов в сети интернет и их возможности Образование в условиях Covid-19
Образование в условиях Covid-19 Текстовый редактор
Текстовый редактор Передача информации, источник и приёмник информации, сигнал, кодирование и декодирование, искажение информации при передаче
Передача информации, источник и приёмник информации, сигнал, кодирование и декодирование, искажение информации при передаче Виртуальная карта госуслуг
Виртуальная карта госуслуг Лукбук
Лукбук Методы и средства сопровождения сайта. Образ организации
Методы и средства сопровождения сайта. Образ организации План покрытия 4G в Балаковском районе
План покрытия 4G в Балаковском районе Использование графического браузера
Использование графического браузера Безопасный интернет
Безопасный интернет Cikl_for для курса (1)
Cikl_for для курса (1) /Мой первый код благотворительный проект игровое программирование для школьников 8-12 лет
/Мой первый код благотворительный проект игровое программирование для школьников 8-12 лет