Содержание
- 2. Двоичная система счисления. Двоичная арифметика *
- 3. Двоичная система счисления Двоичной системой счисления называется позиционная система счисления с основанием 2. Алфавит: 0, 1.
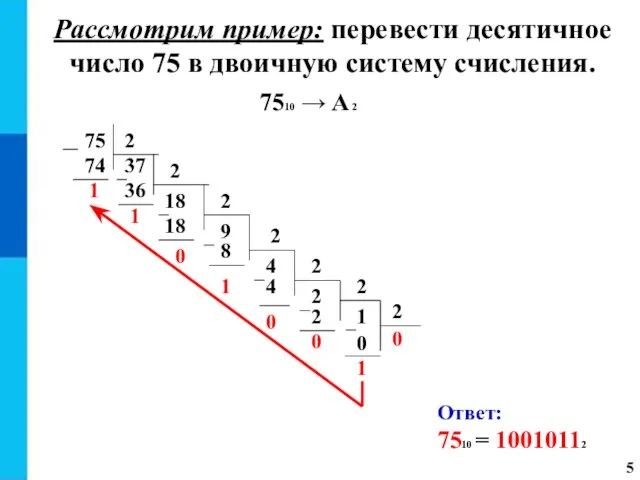
- 4. 1) последовательно выполнять деление данного числа и получаемых целых частных на основание двоичной системы счисления до
- 5. 7510 → A 2 75 2 37 74 1 2 18 36 1 2 9 18
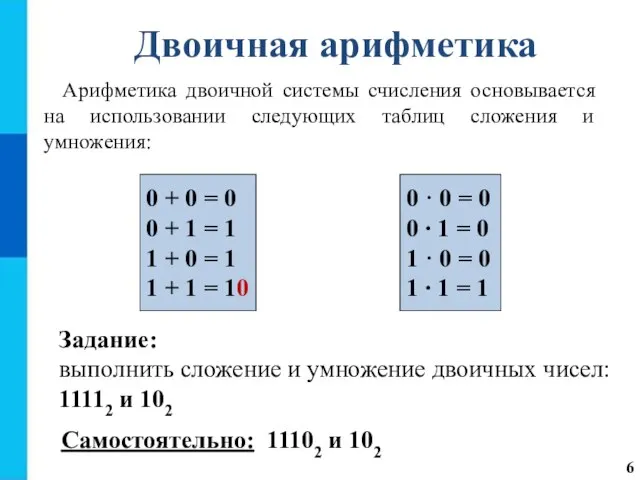
- 6. Двоичная арифметика Арифметика двоичной системы счисления основывается на использовании следующих таблиц сложения и умножения: 0 +
- 8. Скачать презентацию



 Паспорт специальности
Паспорт специальности Инструкция к RadiON Baseband Tool
Инструкция к RadiON Baseband Tool Введение в информационные технологии
Введение в информационные технологии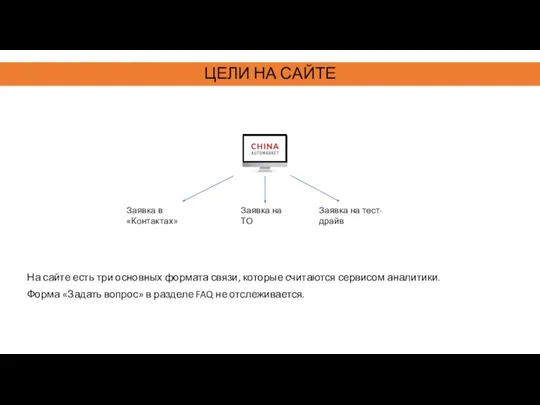 Цели на сайте
Цели на сайте 9-1-4
9-1-4 Тезаурус Безопасный интернет
Тезаурус Безопасный интернет Приложение к положению о конкурсе фоторабот Сибстрин в лицах
Приложение к положению о конкурсе фоторабот Сибстрин в лицах Кодирование информации в компьютере
Кодирование информации в компьютере Язык программирования Python
Язык программирования Python Основные свойства информационных банков СПС
Основные свойства информационных банков СПС лаб работа 1 базы данных
лаб работа 1 базы данных Россия ВКонтакте
Россия ВКонтакте Виды моделирования. Роль моделирования в жизни
Виды моделирования. Роль моделирования в жизни Кодирование текстовой информации
Кодирование текстовой информации Программное обеспечение компьютера
Программное обеспечение компьютера Технологии управления данными
Технологии управления данными Интернет-ресурсы. Подготовка к ЕГЭ по математике
Интернет-ресурсы. Подготовка к ЕГЭ по математике Изучаем C#
Изучаем C# Задача о потоке минимальной стоимости
Задача о потоке минимальной стоимости Практические курсы по Apache Spark для аналитиков, разработчиков, администраторов Big Data
Практические курсы по Apache Spark для аналитиков, разработчиков, администраторов Big Data Основные приемы программирования на языке С++
Основные приемы программирования на языке С++ Информационные таможенные технологии. Лекция 1
Информационные таможенные технологии. Лекция 1 Оформление документов в MS Word
Оформление документов в MS Word Формирование изображения на экране монитора. Обработка графической информации
Формирование изображения на экране монитора. Обработка графической информации Разработка сайта магазина цветов
Разработка сайта магазина цветов Правила безопасного поведения в Интернете
Правила безопасного поведения в Интернете Основы самоорганизующихся сетей
Основы самоорганизующихся сетей Лекция 6
Лекция 6