Класифікація перестановок зі спеціальними властивостями та оцінка потужності класів

Актуальність
Підстановки, що досліджуються в роботі, є підключами найбільш поширених систем криптографічного захисту інформації у ХХ сторіччі - роторних шифрувальних машин
Модифіковані системи роторного шифрування застосовуються і сьогодні
Перестановки та підстановки є базовими криптографічними перетвореннями в сучасних системах захисту інформації, від якості яких залежить стійкість та ефективність систем захисту

Мета, об'єкт та предмет дослідження
Мета дослідження:
класифікація підстановок в ключах роторних шифрувальних машин в залежності від їх криптографічних характеристик
експериментальне отримання статистичних оцінок потужностей класів для підстановок різного розміру
Об'єкт дослідження: ключі зашифрування у роторних машинах та їх модифікаціях
Предмет дослідження: криптографічні характеристики підстановок над алфавітами

Завдання
Провести огляд та аналіз опублікованої літератури за тематикою
Ввести поняття криптографічної характеристики перестановки та запропонувати класифікацію перестановок за їх характеристиками
Створити програму для реалізації розбиття множини усіх перестановок різних розмірів на класи
Методом статистичного моделювання оцінити потужності отриманих класів та ймовірність вибору випадкової перестановки с заданою характеристикою
Перевірити якість оцінки потужності

Перестановки “без перепайок” та їх кількість
Означення. Перестановка (i0, i1, … , in-1) множини {0, 1, … , n-1} є перестановкою “без перепайок”, якщо
∀ k, l ∈ {0, 1, … , n-1}: k + ik (mod n) ≠ l + il (mod n), k ≠ l
Відомі результати та їх автори
Таблиця точних значень Pn для непарних n від 1 до 19 та оцінки Pn для n = 25, 35, 45, 55, ∞
(Cooper C., Gilchrist R., Kovalenko I.N., Novacovic D. - Deriving the number of good permutations with applications to cryptography)
Доведено, що для n ≥ 75: 413.099e-0.9883n ≤ Pn ≤ 267.384e-0.9825n
(Кузнецов Н.Ю. Применение ускоренного моделирования к нахождению количества “хороших” перестановок)

Для заданої перестановки (i0, i1, … , in-1) множини {0, 1, … , n-1} характеристика шукається наступним чином:
Знайти послідовність (j0, j1, … , jn-1), де jm = m + im (mod n)
Представити отриману послідовність у вигляді мультимножини {0k0, 1k1, … , (n-1)kn-1}
Знайти характеристику (α0, α1, … , αn), де α0 – кількість нулів серед чисел km, m=0,1,2,..,n-1, α1 – кількість одиниць і так далі
Побудова характеристики (α0, α1, … , αn)
перестановки (i0, i1, … , in-1)

Властивості характеристик перестановки
Для {k0, k1, … , kn-1):
n
Σ ki = n
i=1
Для (α0, α1, … , αn):
n+1
Σ iαi = n
i=1
Приклади характеристик перестановки
Перестановка без “паралельних перепайок”: (0, n, 0, 0, … , 0)
Перестановка з виродженою характеристикою: (n-1, 0 , … ,0, 1)

Алгоритм генерування випадкової перестановки
Вхід: множина {0, 1, … , n-1}
Для всіх і від n-1 до 1:
Обрати j ∈ {0, 1, … , i} - випадкове число
Поміняти місцями i-тий та j-тий елементи
Вихід: випадкова перестановка

Алгоритм отримання статистичних оцінок потужностей класів
Вхід: множина {0, 1, … , n-1}
Встановити кількість експериментів N - велике число
Поки N ≥ 0:
Побудувати випадкову незалежну перестановку (i0, i1, … , in-1)
Для перестановки (i0, i1, … , in-1) знайти характеристику (α0, α1, … , αn)
Якщо характеристика (α0, α1, … , αn) не зустрічалася на попередніх ітераціях, встановити лічильник с = 1.
Інакше - збільшити с на 1
3. Для кожного отриманого класу за допомогою точкової оцінки с побудувати довірчий інтервал для потужності класу, використовуючи метод Монте-Карло і апроксимацію біноміального розподілу пуассоновим та гауссовим розподілами
Вихід: інтервальні оцінки потужностей класів з різними характеристиками

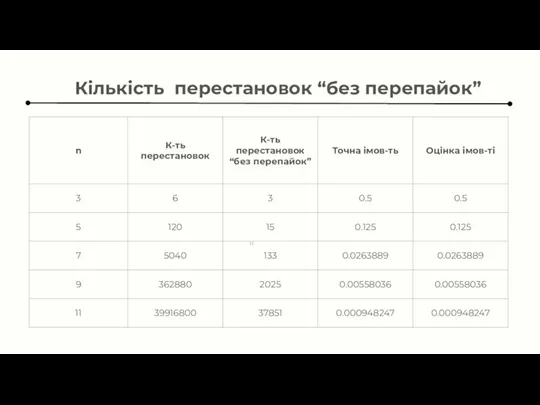
Кількість перестановок “без перепайок”

Порівняння кількості перестановок “без перепайок”

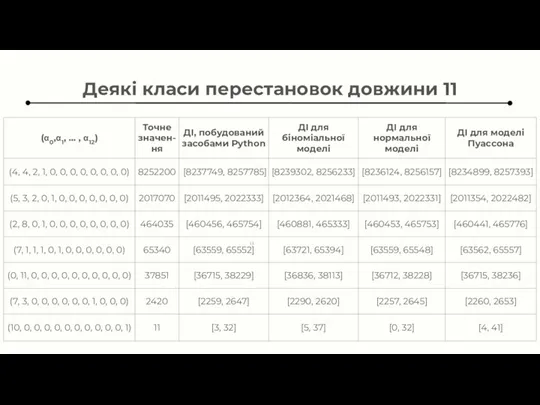
Деякі класи перестановок довжини 11

Характеристики перестановок довжини 26 та 33

Висновки
Введено поняття характеристики перестановки, що узагальнює поняття перестановки “без паралельних перепайок”
Розроблено алгоритм та програма для побудови класів перестановок довільного порядку за їх характеристиками
Методом статистичного моделювання отримано точечні та інтервальні оцінки потужності класів для перестановок довжини 11, 26, 30, 31, 32, 33, 45 та 55 з різними характеристиками. Перевірена якість оцінок.
Показано, що ймовiрнiсть випадково вибрати перестановку з високими криптографiчними властивостями швидко зменшується з ростом порядку перестановки