Компьютерная графика и анимация. Фракталы

Компьютерная графика и анимация
Фракталы (продолжение)
Бельгинова С.А.
[email protected]

Геометрические фракталы. Кривая Коха. Снежинка Коха
Кривая Коха — фрактальная кривая, описанная в 1904 году шведским математиком Хельге фон Кохом. Копии кривой Коха, построенные (остриями наружу) на сторонах правильного треугольника, образуют замкнутую кривую бесконечной длины, называемую снежинкой Коха.

Основные свойства кривой Коха
1. Она непрерывна, но нигде не дифференцируема. Ни в одной точке не имеет касательную.
2. Имеет бесконечную длину.
Пусть длина исходного отрезка равна 1.
На каждом шаге построения мы заменяем каждый из составляющих линию отрезков на ломаную, которая в 4/3 раза длиннее.
Значит, и длина всей ломаной на каждом шаге умножается на 4/3: длина линии с номером n равна (4/3)^(n–1).
3. Снежинка Коха имеет конечную площадь.
Подробный вывод формулы по ссылке:
https://www.youtube.com/watch?v=skKxNSrg8U8&feature=emb_rel_pause

Геометрические фракталы. Системы Линдемайера
L-система это формальная грамматика, используемая для моделирования процессов роста и развития растений.
L-система определяется как кортеж G=(V, w, P),
где V – алфавит, представляющий набор символов, содержащих элементы которые могут быть представлены графически,
w – аксиома, которая представляет собой строку символов из V, определяющая начальное состояния системы,
P - представляет собой набор правил производства новой строки, путем замены символов текущего состояния системы на ряд новых.
Правила грамматики L-системы применяются итеративно, начиная с начального состояния.

Рассмотрим L-систему, где алфавит состоит всего из двух символов
V={a,b}. Аксиома w=a. Правила производства описываются как p1: a→ab, p2: b→ab.
Следуя итеративному принципу, каждое поколение кривой удваивается на каждом этапе: a, ab, abab, abababab. Графически a и b отображаются как два равных отрезка, соединенных под прямым углом.
Рис. 1 - Графическое представление
алфавита L-системы
Системы Линдемайера (продолжение)
Рис. 2 - Графическое представление
правил L-системы

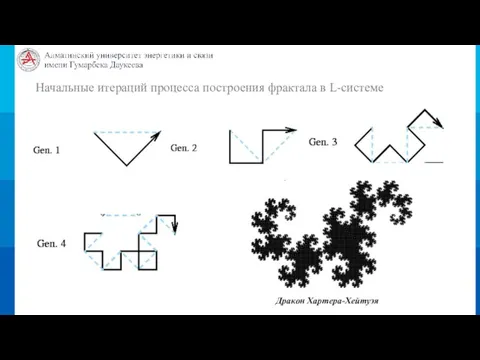
Начальные итераций процесса построения фрактала в L-системе
Дракон Хартера-Хейтуэя

Геометрические фракталы. Треугольник Серпинского
Алгоритм построения:
Равносторонний треугольник M0 делится прямыми, параллельными его сторонам, на 4 равных равносторонних треугольника.
Из треугольника удаляется центральный треугольник.
Получается множество M1, состоящее из 3 оставшихся треугольников "первого ранга".
Поступая точно так же с каждым из треугольников первого ранга, получим множество M2, состоящее из 9 равносторонних треугольников второго ранга.
Продолжая этот процесс бесконечно, получим бесконечную последовательность M0, M1,…, Mn,…пересечение членов которой есть треугольник Серпинского

Линейные геометрические фракталы. Ветвь папортника.
Алгоритм построения основан на подобии построении всей ветви папоротника каждому ее листу. Заключим оригинальное изображение ветви в прямоугольное окно и проведем необходимые линейные и угловые измерения между опорными точками , лежащими на концах ветви и двух нижних листьев.

Составим рекурсивную функцию построения ветви папоротника
Линейные геометрические фракталы. Ветвь папортника. Здесь

Линейные геометрические фракталы. Ветвь папортника.

Алгебраические фракталы
Алгебраические фракталы получают с помощью нелинейных процессов в n-мерных пространствах..
К алгебраическим фракталам относят биоморфы . Термин был предложен Клиффордом Пикоувером для обозначения алгебраических фракталов, внешним видом напоминающих одноклеточные организмы.

Бассейны Ньютона
Рассмотрим уравнение:
Общая формула метода Ньютона имеет вид:
Подставив p(z)p(z) в формулу метода, получим итерационную формулу для построения фрактала:
Подставив p(z) в формулу метода, получим итерационную формулу для построения фрактала:
Итерационный процесс останавливается при:

Бассейны Ньютона
Если записать формулу в общем виде:
то можно получить изображения фракталов более сложной формы:

Алгебраические фракталы. Множество Мендельброта.

Множество Мандельброта

Фрактал Жюлиа
Рассмотрим ту же последовательность комплексных чисел, что и для множества Мандельброта:
Рассматривая множество в общем виде:
Можно получать разнообразные фрактальные множества:

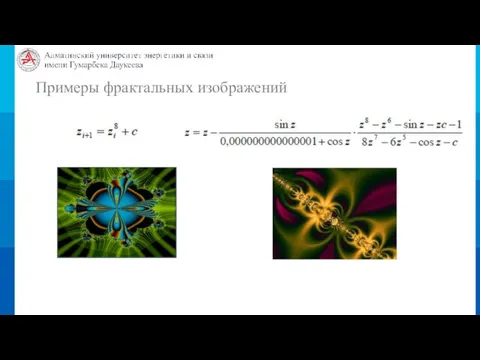
Примеры фрактальных изображений

Примеры фрактальных изображений
“Встреча в аквариуме”.
“Иной”

Примеры фрактальных изображений
“Огненный цветок”
“Сфинкс”

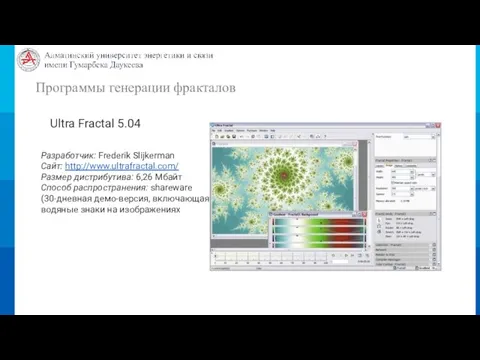
Программы генерации фракталов
Ultra Fractal 5.04
Разработчик: Frederik Slijkerman
Сайт: http://www.ultrafractal.com/
Размер дистрибутива: 6,26 Мбайт
Способ распространения: shareware (30-дневная демо-версия, включающая водяные знаки на изображениях

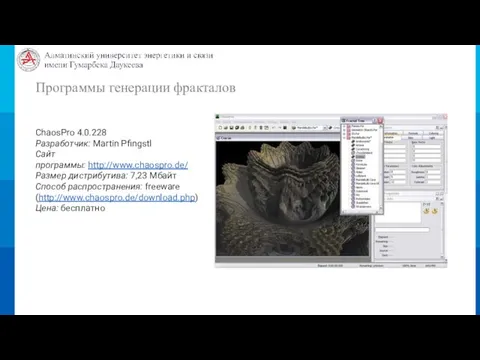
Программы генерации фракталов
ChaosPro 4.0.228
Разработчик: Martin Pfingstl
Сайт программы: http://www.chaospro.de/
Размер дистрибутива: 7,23 Мбайт
Способ распространения: freeware (http://www.chaospro.de/download.php)
Цена: бесплатно

Программы генерации фракталов
XenoDream 2.3
Разработчик: XenoDream Software, LLC
Сайт программы: http://xenodream.com/
Размер дистрибутива: 6,68 Мбайт
Способ распространения: shareware (функционально ограниченная демо-версия, включающая водяные знаки на изображениях

Программы генерации фракталов
Fractracer 1.1
Разработчик: Fractracer Lab
Сайт программы: http://fractracer.com/
Размер дистрибутива: 32-битная версия — 3,5 Мбайт; 64-битная версия — 4 Мбайт
Способ распространения: shareware (функционально ограниченная демо-версия, включающая водяные знаки на изображениях

Программы генерации фракталов
Apophysis 2.02 Stable/2.09 Beta
Разработчик: Peter Sdobnov, Piotr Borys, Ronald Hordijk
Сайт программы: http://www.apophysis.org/
Размер дистрибутива: 2,58 Мбайт
Способ распространения: freeware

Программы генерации фракталов
Fractal Extreme 2.04
Разработчик: Cygnus Software
Сайт программы: http://www.cygnus-software.com/
Размер дистрибутива: 32-битная версия — 12 Мбайт; 64-битная версия — 10,63 Мбайт
Способ распространения: shareware (15-дневная демо-версия

Программы генерации фракталов
Chaoscope 0.3.1
Разработчик: Chaoscope Team
Сайт программы: http://www.chaoscope.org/
Размер дистрибутива: 2,5 Мбайт
Способ распространения: freeware

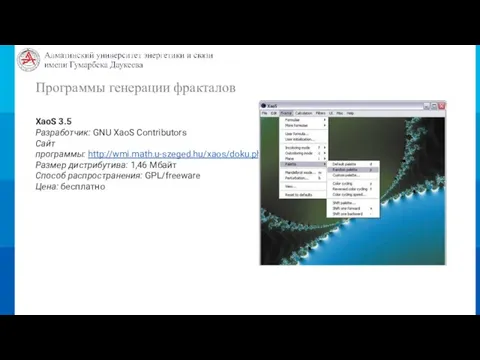
Программы генерации фракталов
XaoS 3.5
Разработчик: GNU XaoS Contributors
Сайт программы: http://wmi.math.u-szeged.hu/xaos/doku.php
Размер дистрибутива: 1,46 Мбайт
Способ распространения: GPL/freeware Цена: бесплатно