Слайд 2Простое число
Это Натуральное число, имеющее ровно два различных натуральных делителя - единицу

и самого себя.
Слайд 4Взаимно-простые числа
Целые числа взаимно просты, если их наибольший общий делитель равен 1.

Например, взаимно просты числа 14 и 25, так как у них нет общих делителей; но числа 15 и 25 не взаимно просты, так как у них имеется общий делитель 5.
Слайд 5Сравнение
Целые числа a и b называют сравнимыми по модулю m, если каждое

из них при делении на m дает один и тот же остаток r.
r ≡ a (mod m ).
r ≡ b (mod m ).
То есть существует такое число t такое , что выполняется равенство
r ≡ a + m*t
r ≡ b + m*t
Пример:
125 ≡ 13(mod 16 )
Или
125 = 13 + 16*t, где если t=7, выполнено равенство
Слайд 7Теорема
В любой части сравнения можно отбросить или добавить слагаемое, кратное модулю.
Пример
13
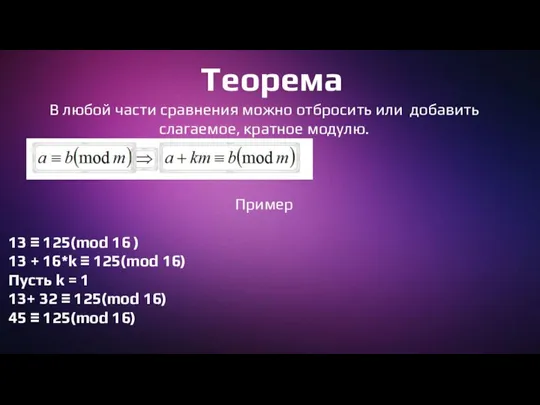
≡ 125(mod 16 )
13 + 16*k ≡ 125(mod 16)
Пусть k = 1
13+ 32 ≡ 125(mod 16)
45 ≡ 125(mod 16)
Слайд 8Доказательство
Представим сравнение в виде уравнения с одной переменной:
45 = 125 + m*t

Если взять t = -5 получим:
45 = 125 – 5*16
Верно
Слайд 9Задачи
1)Найдите остаток от деления 229 на 11.
2) Найдите остаток от деления 3412

на 11
3)Найдите остаток от деления 229 на 11.
Слайд 10Функция Эйлера
(функция Эйлера) – это количество чисел из ряда 0,1,2,3,…,n-1, взаимнопростых с

числом «n»
Любое число можно представить в виде множителей состоящих из простых чисел
n = p1a1*p2a2*…*pkak
= n * (1- 1/p1)* (1- 1/p2)* (1- 1/p3)* … * (1- 1/pk)
в
Слайд 11Теорема Эйлера
Пусть m > 1, НОД(a,m) = 1, ϕ(m)-функция Эйлера
Справедливо следующее

aϕ(m) ≡ 1 (mod m)
Теорема Ферма:
Пусть p – простое число и оно не делит «а», то верно следующее:
ap-1= 1 (mod p)
Слайд 12Задачи
1)Девятая степень однозначного числа оканчивается на цифру 7
2) Найти 2 последние цифры

числа 243402
3)Доказать что:
118+ 218+ 318+ 418+ 518+ 618 ≡ -1(mod 7)
Слайд 13Алгоритм Евклида
Для нахождения наибольшего общего делителя двух чисел a и b

(a и b – целые положительные числа, причем a больше или равно b) последовательно выполняется деление с остатком, которое дает ряд равенств вида
Суть алгоритма заключается в том, чтобы последовательно проводить деление с остатком.
Представим а = b*q+r ,
НОД(a,b) = НОД(b,r) и так далее пока вторым число не будет ноль
НОК(a,b)= (a*b)/НОД(a,b)
Слайд 14Алгоритм Евклида
Пример:
Найдите наибольший общий делитель чисел 64 и 48.
Решение
Введем обозначения:

a = 64 , b = 48
НОД(64,48)= НОД(48,(64mod48))=НОД(16,(48mod16))=НОД(16,0)
Ответ: Наибольший общий делитель равен 16
Слайд 15Теорема Безу
Если «а» и «b» не равны 0, то существуют такие коэффициенты

«x» и «y», такие что:
НОД(a,b)=a*x+b*y




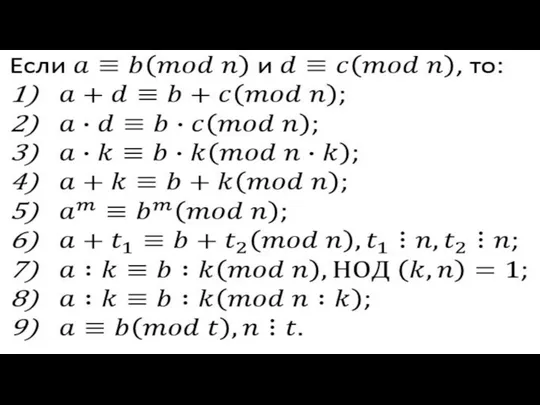









 Циклы, массивы, таблицы
Циклы, массивы, таблицы Графическая информация в Интернет
Графическая информация в Интернет Лекция 1
Лекция 1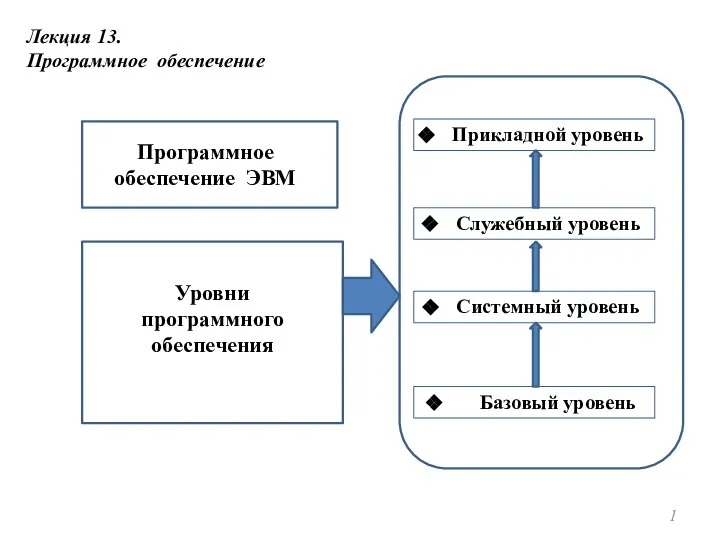 Программное обеспечение
Программное обеспечение Медиаплееры
Медиаплееры Сравнительный анализ сайтов
Сравнительный анализ сайтов Презентация на тему Двумерные массивы
Презентация на тему Двумерные массивы 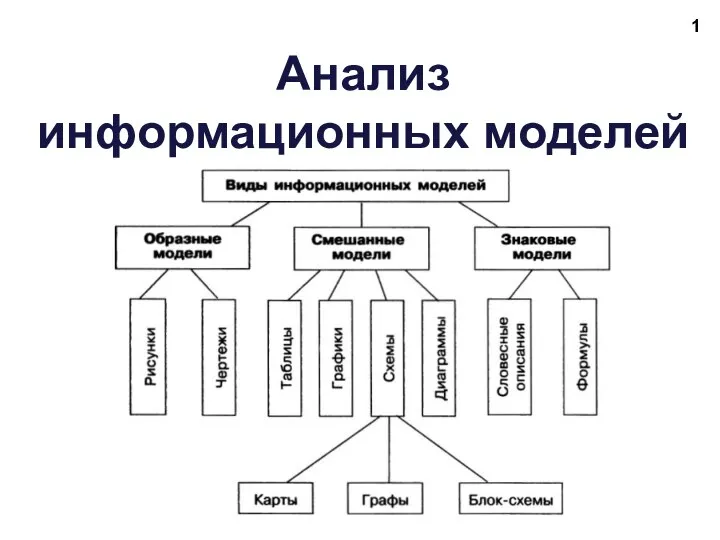 Матрица смежности. Анализ информационных моделей
Матрица смежности. Анализ информационных моделей От истоков до наших дней. Objective C
От истоков до наших дней. Objective C Масштабні революційні інновації на телебаченні, в Інтернеті і в пресі на базі розробок в рамках Міжнародного проекту Краса
Масштабні революційні інновації на телебаченні, в Інтернеті і в пресі на базі розробок в рамках Міжнародного проекту Краса Компьютерные сети. Тема 2
Компьютерные сети. Тема 2 Алгоритмическая конструкция ветвление. Основные алгоритмические конструкции
Алгоритмическая конструкция ветвление. Основные алгоритмические конструкции Спиральная модель управление проектами в IT
Спиральная модель управление проектами в IT Generic Sensor API
Generic Sensor API Организация ввода и вывода данных
Организация ввода и вывода данных Системный анализ в ГМУ
Системный анализ в ГМУ Факторы, снижающие пропускную способность вычислительных систем
Факторы, снижающие пропускную способность вычислительных систем Адаптация известных форм квестов для еврейского образования
Адаптация известных форм квестов для еврейского образования Голографическая защита информации
Голографическая защита информации Popular minimalist decluttering method
Popular minimalist decluttering method Создание компьютерной модели 312.18.14 Клин
Создание компьютерной модели 312.18.14 Клин Рязань - колыбель космонавтики
Рязань - колыбель космонавтики Вечная тетрадь, надежно хранит Ваши записи в облаке
Вечная тетрадь, надежно хранит Ваши записи в облаке Основные этапы работы над веб-сайтом
Основные этапы работы над веб-сайтом Размещение виджета организации
Размещение виджета организации Кодирование данных и структуры данных
Кодирование данных и структуры данных Flowers memory
Flowers memory Массивы
Массивы