Содержание
- 2. Логика — это наука о формах и способах мышления. Это учение о способах рассуждений и доказательств.
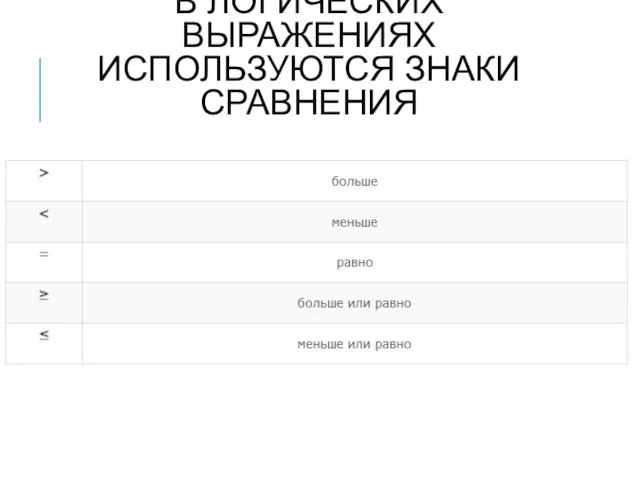
- 3. В ЛОГИЧЕСКИХ ВЫРАЖЕНИЯХ ИСПОЛЬЗУЮТСЯ ЗНАКИ СРАВНЕНИЯ
- 4. Алгебра логики (Булева алгебра) Используется для работы с двоичным кодом. Джордж Буль разработал основы алгебры, в
- 5. Логические высказывания Логическое высказывание – это повествовательное предложение, которое может быть истинно или ложно (однозначный ответ).
- 6. Простое высказывание содержит только одну мысль. Это логическая переменная. Обозначение — латинская буква (например, A, B,
- 7. Обозначение высказываний A – Сейчас идет дождь. B – Форточка открыта. простые высказывания (элементарные) Составные высказывания
- 8. Логические операции — логическое действие. При создании ЭВМ были использованы 3 основные операции: НЕ И ИЛИ
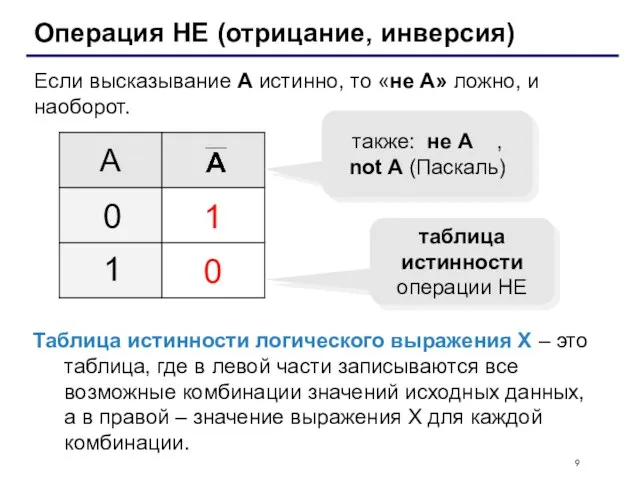
- 9. Операция НЕ (отрицание, инверсия) Если высказывание A истинно, то «не А» ложно, и наоборот. 1 0
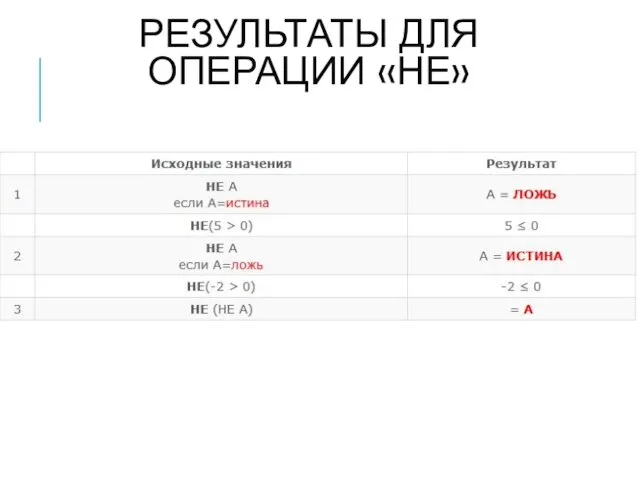
- 10. РЕЗУЛЬТАТЫ ДЛЯ ОПЕРАЦИИ «НЕ»
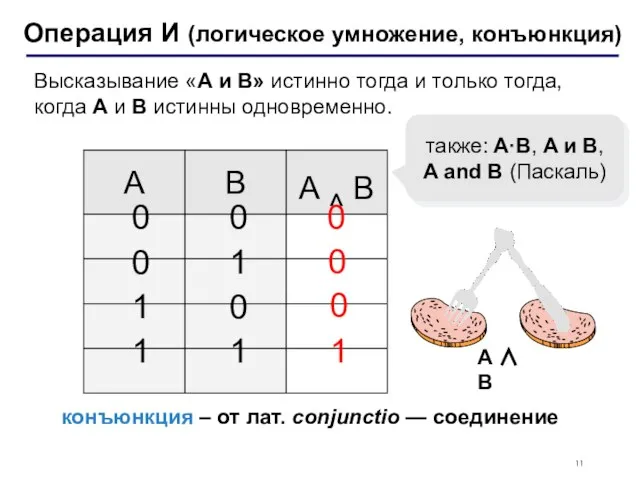
- 11. Операция И (логическое умножение, конъюнкция) 1 0 также: A·B, A и B, A and B (Паскаль)
- 12. РЕЗУЛЬТАТЫ ДЛЯ ОПЕРАЦИИ «И»
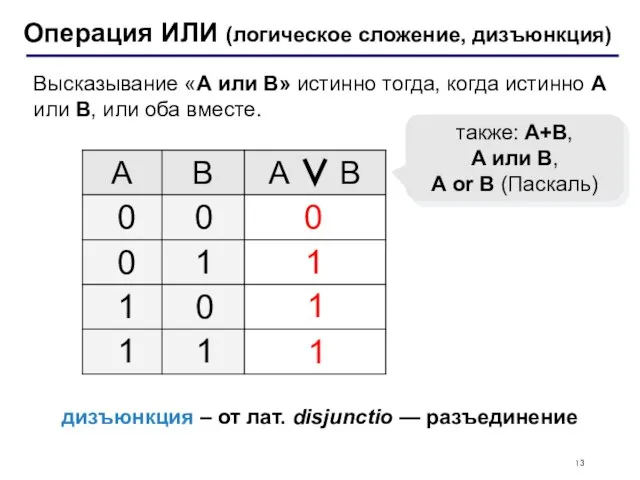
- 13. Операция ИЛИ (логическое сложение, дизъюнкция) 1 0 также: A+B, A или B, A or B (Паскаль)
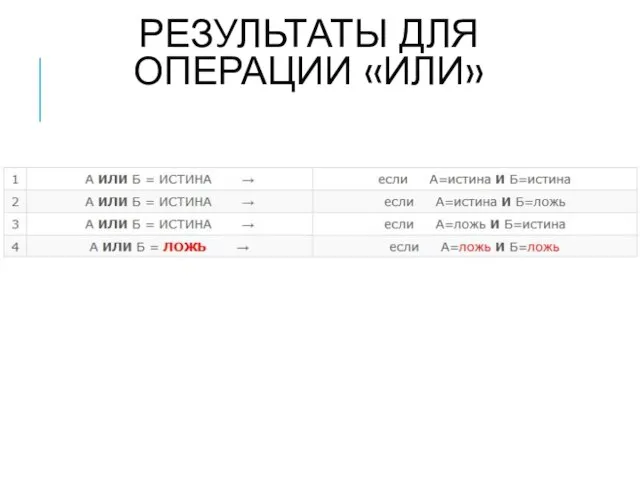
- 14. РЕЗУЛЬТАТЫ ДЛЯ ОПЕРАЦИИ «ИЛИ»
- 15. При составлении логического выражения необходимо учитывать порядок выполнения логических операций: 1. Отрицание (НЕ) 2.Выражение в скобках
- 16. Если отрицание НЕ стоит перед скобкой с выражением, то НЕ ставится перед каждой частью выражения в
- 17. ПРИМЕР 1 Напишите наибольшее целое число x, для которого истинно высказывание: (X > 5) И НЕ
- 18. РЕШЕНИЕ 1.Выполним первую по приоритету операцию — операцию НЕ: НЕ (X > 15) 2.Получаем (X 3.Т.е.
- 19. ПРИМЕР 2
- 20. РЕШЕНИЕ
- 21. ПРОВЕРОЧНАЯ РАБОТА
- 22. Задание №1
- 23. Задание №2
- 24. Задание №3
- 26. Скачать презентацию

















 Оптимизация процессов публично-правовой организации
Оптимизация процессов публично-правовой организации Презентация на тему Действия с фрагментом текста
Презентация на тему Действия с фрагментом текста  Инициатива A
Инициатива A Презентация на тему Безопасность в сети интернет для 5-6 классов
Презентация на тему Безопасность в сети интернет для 5-6 классов  Boardgamearena — сайт, позволяющий играть в разнообразные настольные игры прямо из дома
Boardgamearena — сайт, позволяющий играть в разнообразные настольные игры прямо из дома ec8f84f81f5c61f5
ec8f84f81f5c61f5 Электронные таблицы или табличные процессоры
Электронные таблицы или табличные процессоры Библиотека и читатель: вместе по жизни
Библиотека и читатель: вместе по жизни «Счастливый случай» Тема: Системы счисления и Информационные процессы
«Счастливый случай» Тема: Системы счисления и Информационные процессы Curtis. Mood board
Curtis. Mood board Электронные таблицы. Обработка числовой информации в электронных таблицах
Электронные таблицы. Обработка числовой информации в электронных таблицах Алгоритмы шифрования
Алгоритмы шифрования Компьютерные вирусы
Компьютерные вирусы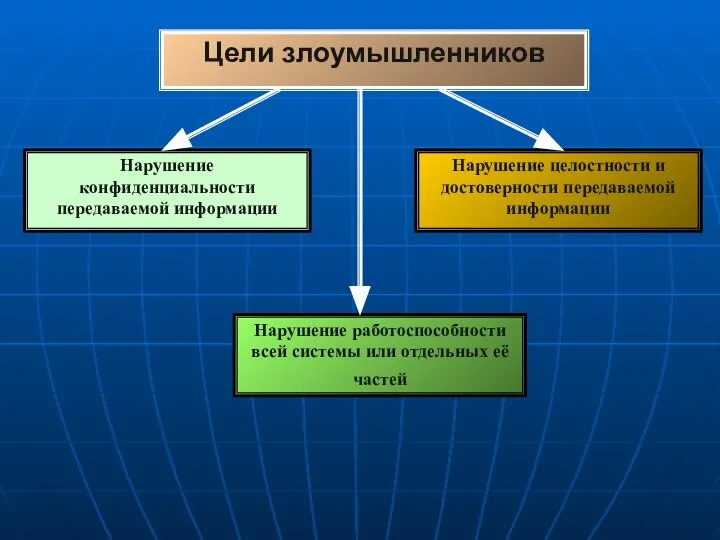 Цели злоумышленников
Цели злоумышленников Безопасное и рациональное использование личных и персональных данных в интернет-пространстве. Занятие 6
Безопасное и рациональное использование личных и персональных данных в интернет-пространстве. Занятие 6 Проблемы построения электронного документооборота и принципы его реализации
Проблемы построения электронного документооборота и принципы его реализации Характеристика процесса проектирования ВУ
Характеристика процесса проектирования ВУ Особенности работы с пакетом SPSS (Statistical Package for the Social Science)
Особенности работы с пакетом SPSS (Statistical Package for the Social Science) Продвижение личного бренда
Продвижение личного бренда Особенности градостроительного кадастра
Особенности градостроительного кадастра Встроенные объекты JavaScript
Встроенные объекты JavaScript Документооборот
Документооборот Скриншот история подключений
Скриншот история подключений Проведение урока он-лайн на платформе Zoom
Проведение урока он-лайн на платформе Zoom История развития Windows 2000
История развития Windows 2000 Язык программирования Python. Основные встроенные модули
Язык программирования Python. Основные встроенные модули ВПД 2020. Тема2. Информационные системы и технологии
ВПД 2020. Тема2. Информационные системы и технологии Получение сведений из фонда данных государственной кадастровой оценки
Получение сведений из фонда данных государственной кадастровой оценки