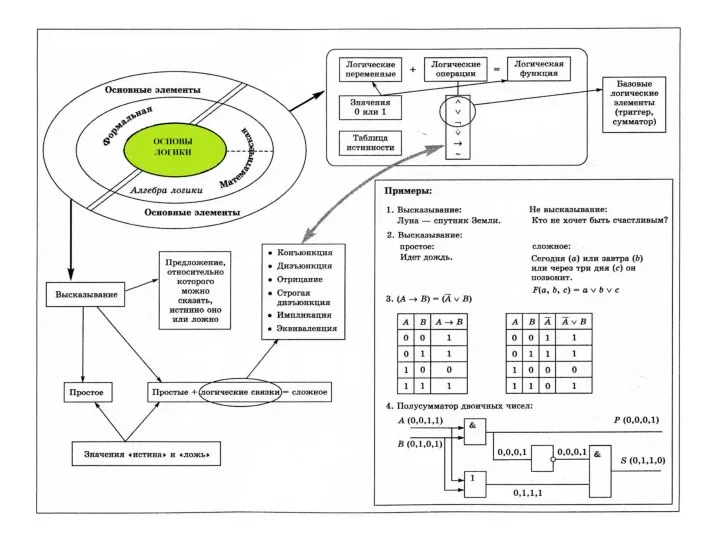
Содержание
- 3. Алгебра логики устанавливает законы мышления. Основные формы мышления: понятие, суждение (высказывание), умозаключение. Понятие выделяет существенные признаки
- 4. 2. Этапы развития логики Основоположник логики как науки - древнегреческий философ и ученый Аристотель (384-322 гг.
- 5. Демокрит Платон Евклид Первый этап – формальная логика ( работы древнегреческих ученых: Аристотель, Платон, Демокрит). 1.
- 6. Рене Декарт Готфрид А. Лейбниц Джордж Буль Второй этап – математическая или символьная логика. Основоположник -
- 7. Клод Элвуд Шеннон Американский математик и инженер. Применил булеву алгебру к теории электрических цепей «Отец» современной
- 8. Операция, выражаемая словом «не», называется отрицанием и обозначается чертой над высказыванием (или знаком ¬). Высказывание ¬А
- 9. Операция, выражаемая связкой «или» называется дизъюнкцией или логическим сложением и обозначается знаком ∨ или +. Высказывание
- 10. Операция, выражаемая связками «если…, то», «из…следует», «влечет…», называется импликацией и обозначается знаком →. Высказывание А→В ложно
- 11. Операция, выражаемая связками «тогда и только тогда», «необходимо и достаточно», «…равносильно…», называется эквиваленцией или двойной импликацией
- 12. Очень важными для вычислительной техники являются операции исключающее ИЛИ (неравнозначность, сложение по модулю два) и штрих
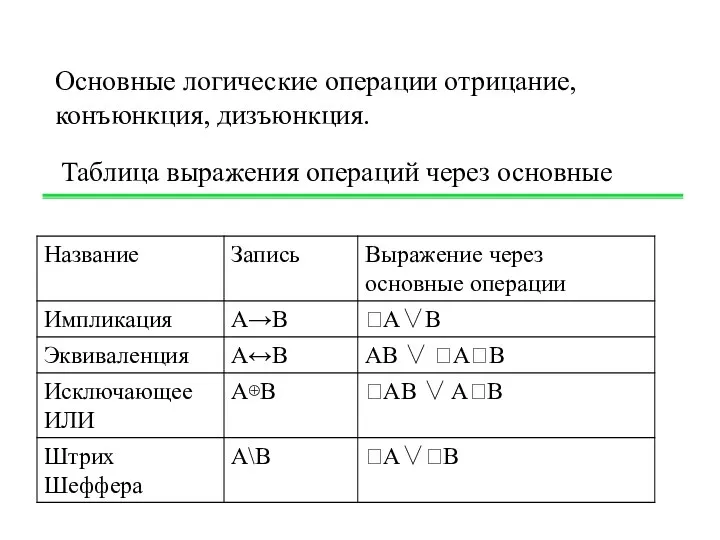
- 13. Основные логические операции отрицание, конъюнкция, дизъюнкция. Таблица выражения операций через основные
- 14. Определение логической формулы. 1. Всякая логическая переменная и символы истина и ложь – формулы. 2. Если
- 15. Формула, которая при одних сочетаниях входящих в нее переменных является истинной, а при других – ложной,
- 16. Формула, которая ложна при любых значениях истинности входящих в нее переменных, называется тождественно-ложной или противоречивой. Например,
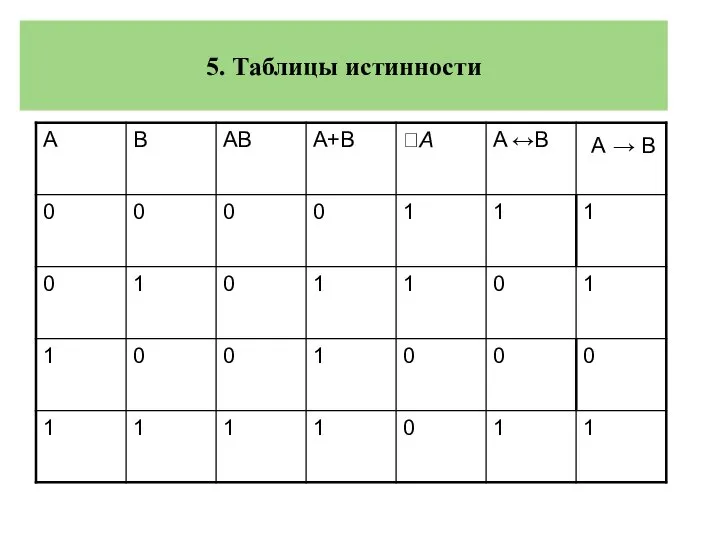
- 17. 5. Таблицы истинности
- 18. 6. Аксиомы и законы алгебры логики Система аксиом алгебры логики х=0, если х ≠ 1. х=1,
- 19. Тождества алгебры логики х ∨ х = 1 х ^ х = 0 0 ∨ х
- 20. 1. Закон исключения третьего. Был известен уже в древности. Содержательная трактовка: «Во время своих странствований Платон
- 21. 2. Закон непротиворечивости. Если сказать: «Во время своих странствий Платон был в Египте И не был
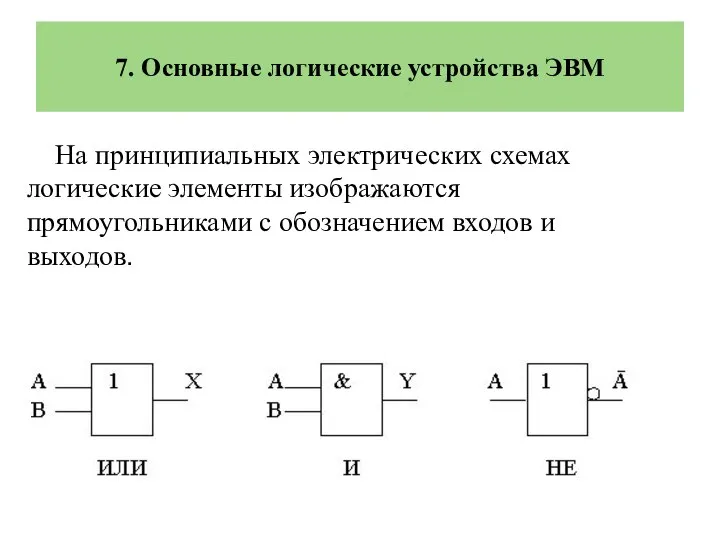
- 22. На принципиальных электрических схемах логические элементы изображаются прямоугольниками с обозначением входов и выходов. 7. Основные логические
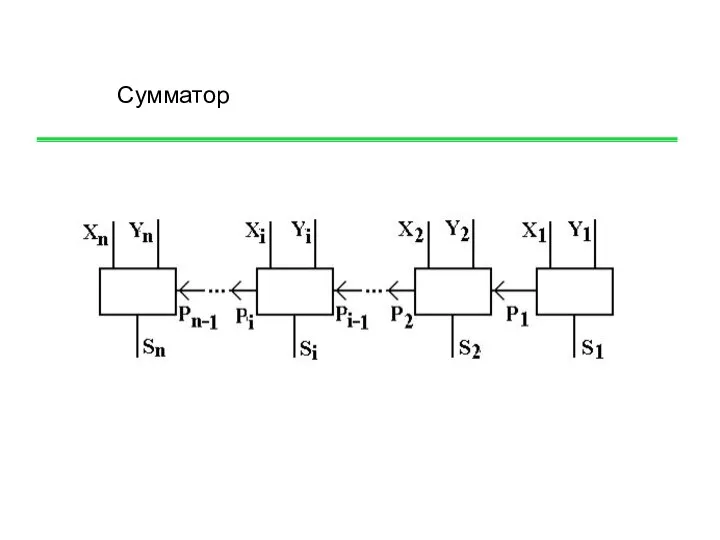
- 23. Сумматор
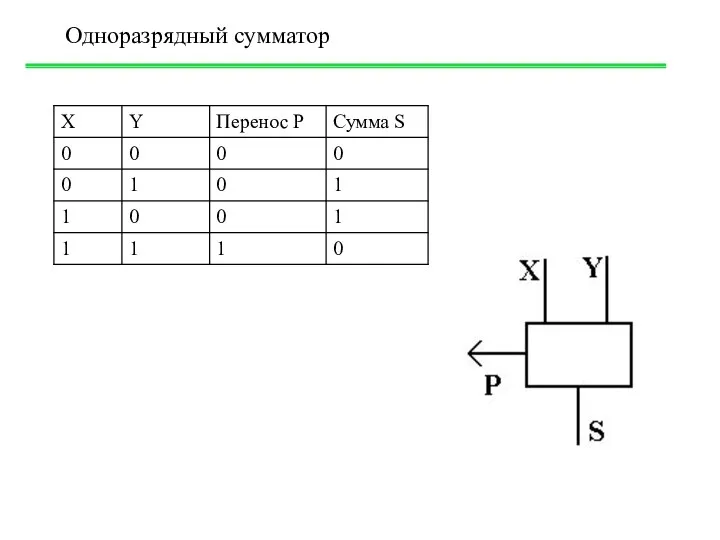
- 24. Одноразрядный сумматор
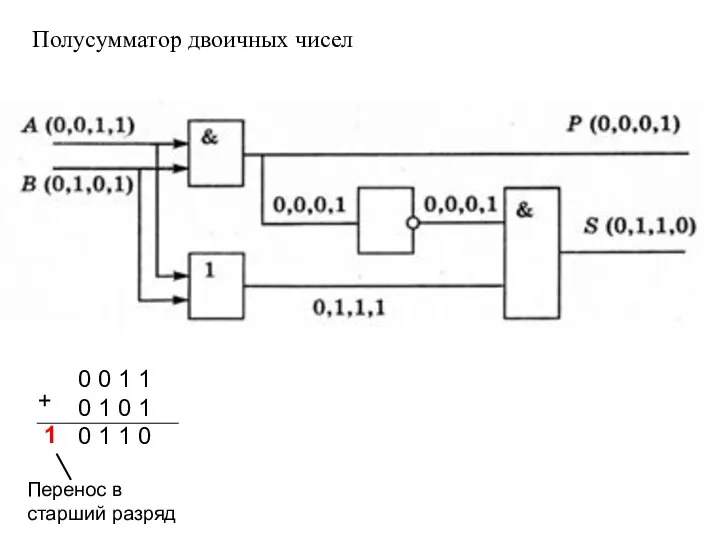
- 25. Полусумматор двоичных чисел 0 0 1 1 0 1 0 1 0 1 1 0 +
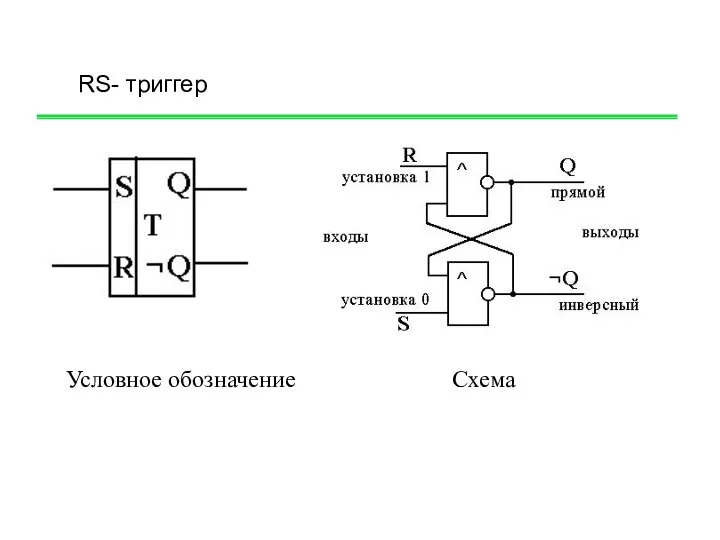
- 26. Условное обозначение Схема RS- триггер
- 28. Скачать презентацию

















 Свинограм
Свинограм Лекция 1
Лекция 1 Системы счисления. Математические основы информатики
Системы счисления. Математические основы информатики Модель Захмана
Модель Захмана Система управления НТД и требованиями. Техэксперт
Система управления НТД и требованиями. Техэксперт Рекурсивный перебор. Алгоритмизация и программирование, язык Python
Рекурсивный перебор. Алгоритмизация и программирование, язык Python Цвета. Урок 10
Цвета. Урок 10 Вычисление площади поверхности конуса в табличном процессоре MS Excel
Вычисление площади поверхности конуса в табличном процессоре MS Excel Microprocessor-Based Systems
Microprocessor-Based Systems Текстовый редактор
Текстовый редактор Комплектование документного фонда в библиотеке
Комплектование документного фонда в библиотеке Компьютер. Процессор и память. Устройства ввода. Устройства вывода
Компьютер. Процессор и память. Устройства ввода. Устройства вывода Технология построения диаграммы Варианты использования в UML
Технология построения диаграммы Варианты использования в UML Мой графический редактор
Мой графический редактор Эффективные мобильные приложения для изучения английского языка
Эффективные мобильные приложения для изучения английского языка Cети ЦВМ - системообразующий элемент сложных технических систем
Cети ЦВМ - системообразующий элемент сложных технических систем Адресация в интернете
Адресация в интернете Сообщение по методу Цезаря
Сообщение по методу Цезаря Исследователи читальных залов: готовность к новым технологиям и краудсорсингу
Исследователи читальных залов: готовность к новым технологиям и краудсорсингу Уровневая модель ISO
Уровневая модель ISO Услуги компьютерных сетей. Удаленная база данных
Услуги компьютерных сетей. Удаленная база данных Сети, их виды. Топология сетей. Лекция 5
Сети, их виды. Топология сетей. Лекция 5 Обработка фото в Lightroom
Обработка фото в Lightroom Растровая и векторная графика
Растровая и векторная графика Анализ соцсети
Анализ соцсети Тест по информатике
Тест по информатике Разработка дополнительного программного модуля для конфигурации 1с предприятие
Разработка дополнительного программного модуля для конфигурации 1с предприятие Презентація (1)
Презентація (1)