Содержание
- 2. Логика, высказывания Логика (др.греч. λογικος) – это наука о том, как правильно рассуждать, делать выводы, доказывать
- 3. Высказывание или нет? Сейчас идет дождь. Жирафы летят на север. История – интересный предмет. У квадрата
- 4. Логика и компьютер Двоичное кодирование – все виды информации кодируются с помощью 0 и 1. Задача
- 5. Обозначение высказываний A – Сейчас идет дождь. B – Форточка открыта. простые высказывания (элементарные) Составные высказывания
- 6. Операция НЕ (инверсия) Если высказывание A истинно, то «не А» ложно, и наоборот. 1 0 0
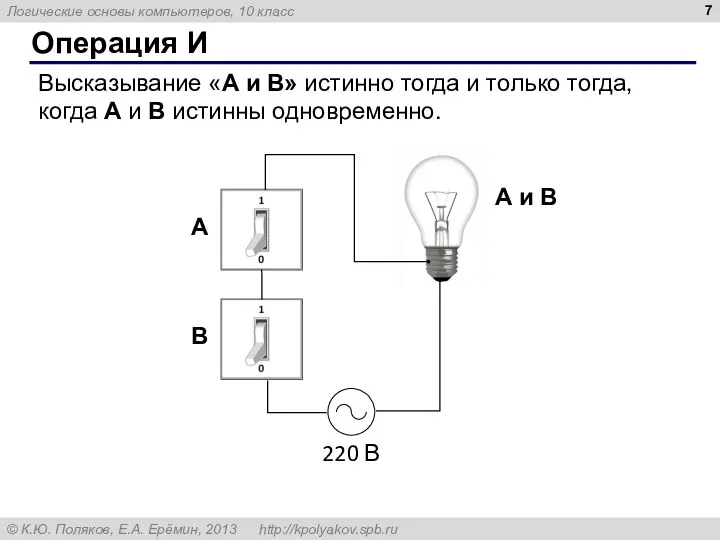
- 7. Операция И Высказывание «A и B» истинно тогда и только тогда, когда А и B истинны
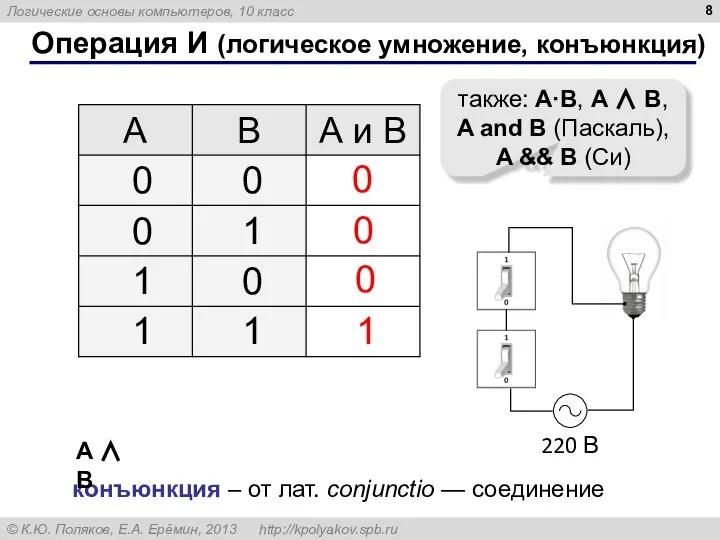
- 8. Операция И (логическое умножение, конъюнкция) 1 0 также: A·B, A ∧ B, A and B (Паскаль),
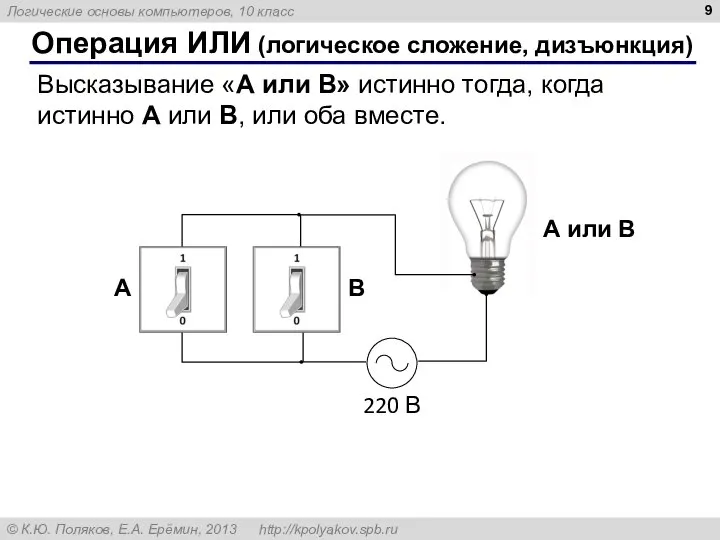
- 9. Операция ИЛИ (логическое сложение, дизъюнкция) Высказывание «A или B» истинно тогда, когда истинно А или B,
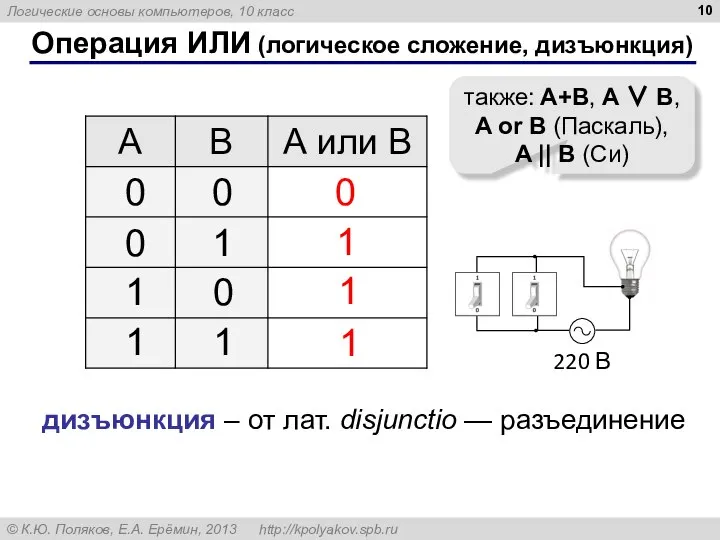
- 10. Операция ИЛИ (логическое сложение, дизъюнкция) 1 0 также: A+B, A ∨ B, A or B (Паскаль),
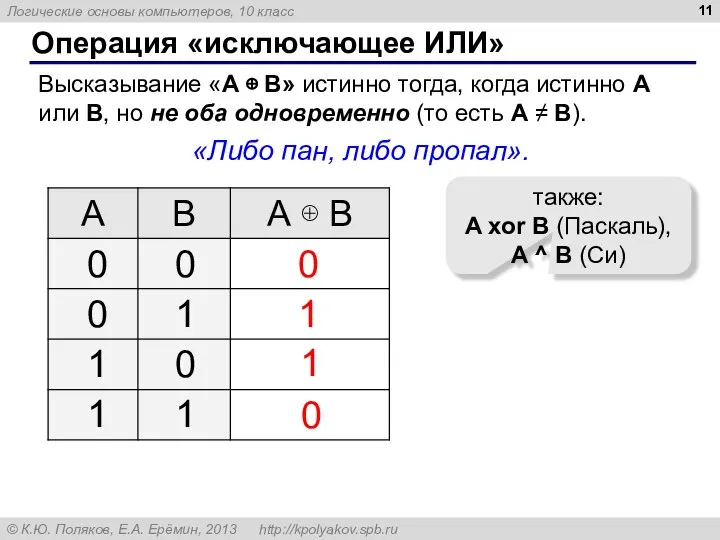
- 11. Операция «исключающее ИЛИ» Высказывание «A ⊕ B» истинно тогда, когда истинно А или B, но не
- 12. Импликация («если …, то …») Высказывание «A → B» истинно, если не исключено, что из А
- 13. Импликация («если …, то …») «Если Вася идет гулять, то Маша сидит дома». A – «Вася
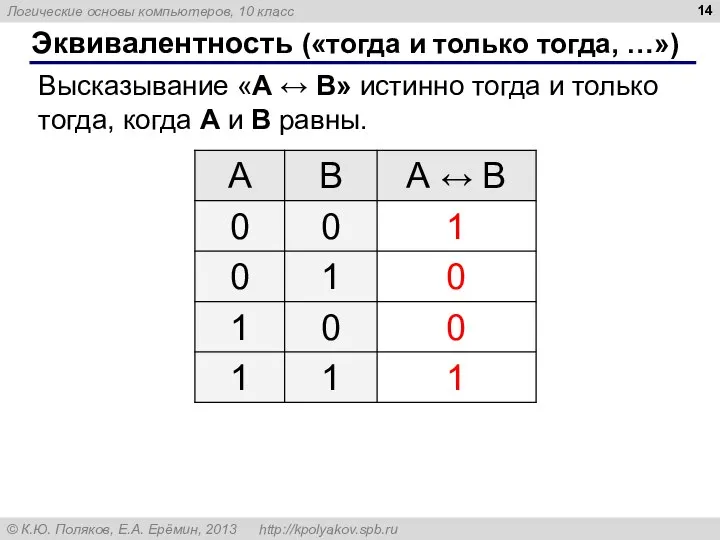
- 14. Эквивалентность («тогда и только тогда, …») Высказывание «A ↔ B» истинно тогда и только тогда, когда
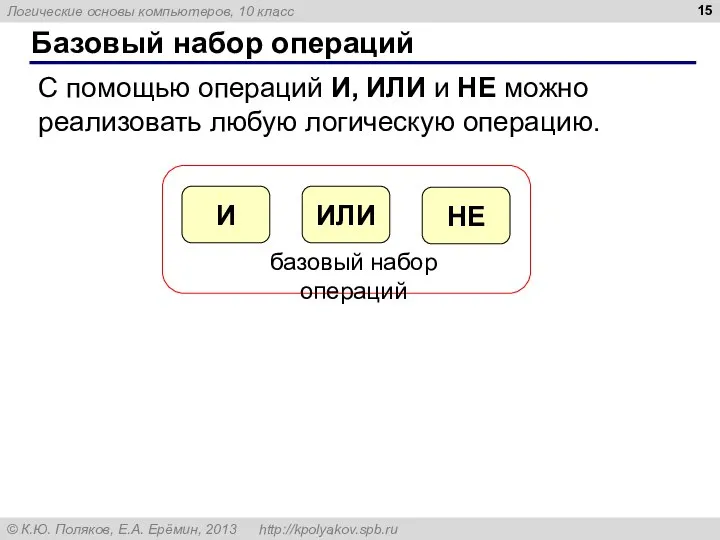
- 15. Базовый набор операций С помощью операций И, ИЛИ и НЕ можно реализовать любую логическую операцию.
- 16. Вычисление логических выражений Порядок вычислений: скобки НЕ И ИЛИ, исключающее ИЛИ импликация эквивалентность 1 4 2
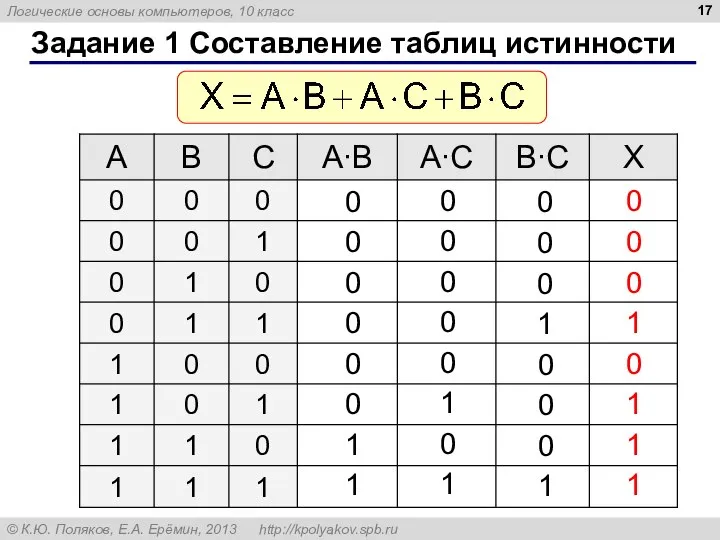
- 17. Задание 1 Составление таблиц истинности
- 18. Задание 2. Какие из приведенных слов удовлетворяют логическому условию: (первая буква согласная→вторая буква согласная) & (последняя
- 19. Задание 3 Построить таблицу истинности a ∧ ¬b ∨ (a ∨ b) ∧ c
- 21. Скачать презентацию










 Web-программирование. Лекция 5. Шаблоны проектирования
Web-программирование. Лекция 5. Шаблоны проектирования Правила работы и безопасного поведения в компьютерном классе
Правила работы и безопасного поведения в компьютерном классе Использование облачных технологий в деятельности педагога
Использование облачных технологий в деятельности педагога Известия VS Медиазона
Известия VS Медиазона Аудит divine-light.ru_версия 21092022
Аудит divine-light.ru_версия 21092022 Основы музейных коммуникаций
Основы музейных коммуникаций Internet Protocol (IP)
Internet Protocol (IP) ВКонтакте - российская социальная сеть
ВКонтакте - российская социальная сеть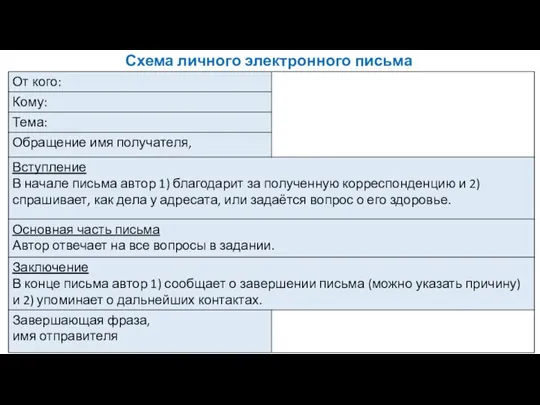 Схема личного электронного письма
Схема личного электронного письма Мобильное электронное образование в детских садах и дома
Мобильное электронное образование в детских садах и дома Базовые показатели эффективности (БПЭ)
Базовые показатели эффективности (БПЭ) Представление звуковой информации
Представление звуковой информации Технология промышленного производства
Технология промышленного производства Сеть для организаций. Отчет о проектной работе
Сеть для организаций. Отчет о проектной работе Умные таблицы Excel 2007-2013
Умные таблицы Excel 2007-2013 Строки как одномерные массивы данных типа char (терминальные строки)
Строки как одномерные массивы данных типа char (терминальные строки) Азбука журналистики
Азбука журналистики Краудсорсинг в ИТ рекрутменте
Краудсорсинг в ИТ рекрутменте Метрология и теория измерений
Метрология и теория измерений одирование тестовой, графической и звуковой информации
одирование тестовой, графической и звуковой информации Вводное занятие. Система отслеживания багов и задач JIRA (лекция - 3)
Вводное занятие. Система отслеживания багов и задач JIRA (лекция - 3) Инструкция по входу в ZOOM
Инструкция по входу в ZOOM Das At-Zeichen
Das At-Zeichen Презентация на тему Поколение ЭВМ
Презентация на тему Поколение ЭВМ  Понятие информация
Понятие информация Web - страницы. Язык HTML
Web - страницы. Язык HTML Ресурсы для защиты информации в веке IT технологий
Ресурсы для защиты информации в веке IT технологий Одномерные массивы целых чисел. Описание, заполнение, вывод массива
Одномерные массивы целых чисел. Описание, заполнение, вывод массива