задачи на оптимальность;
B. один из комбинированных методов дискретного программирования, при котором гиперплоскость, определяемая целевой функцией задачи, вдавливается внутрь многогранника планов соответствующей задачи линейного программирования до встречи с ближайшей целочисленной точкой этого многогранника;
C. один из методов отсечения, с помощью которого решаются задачи целочисленного программирования;
D. один из группы методов определения первоначального опорного плана транспортной задачи.
5) Оптимальный план задачи линейного программирования это
A. решение задачи линейного программирования, т. е. такой план, который не входит в допустимую область и доставляет экстремум целевой функции;
B. решение задачи линейного программирования, т. е. такой план, который входит в допустимую область и доставляет ненулевое значение целевой функции;
C. решение задачи линейного программирования, т. е. такой план, который входит в допустимую область и доставляет нулевое значение целевой функции;
D. решение задачи линейного программирования, т. е. такой план, который входит в допустимую область и доставляет экстремум целевой функции.
Примеры тестовых заданий для проверки знаний




























 Тестовая программа по информатике
Тестовая программа по информатике Использование презентаций на уроках литературного чтения
Использование презентаций на уроках литературного чтения Blu-ray. Преимущества Blu-ray
Blu-ray. Преимущества Blu-ray Bilgisayar ağları ve iletişim. Ip adres tanimlamalari ve siniflari, alt ağlar, ipv6. (4.hafta)
Bilgisayar ağları ve iletişim. Ip adres tanimlamalari ve siniflari, alt ağlar, ipv6. (4.hafta) Лекция6
Лекция6 Турнир кибермании
Турнир кибермании Аппаратура информатизации образования
Аппаратура информатизации образования Концепция ERP-системы 1С:Управление предприятием
Концепция ERP-системы 1С:Управление предприятием Організація пам'яті комп'ютера. Прості схеми управління пам'яттю. Тема 3.1
Організація пам'яті комп'ютера. Прості схеми управління пам'яттю. Тема 3.1 Использование систем мгновенного обмена сообщениями в процессе иноязычной подготовки студентов на примере сервиса Discord
Использование систем мгновенного обмена сообщениями в процессе иноязычной подготовки студентов на примере сервиса Discord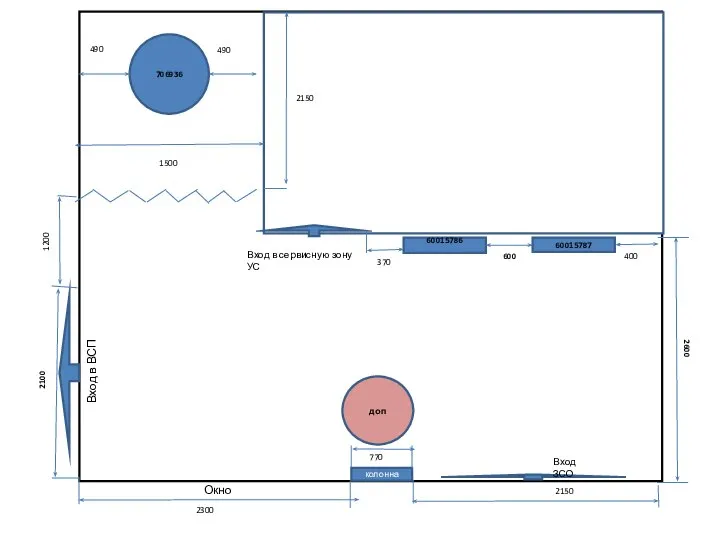 План зсо
План зсо лаб работа 1 базы данных
лаб работа 1 базы данных Web-программирование. Основы Node.js
Web-программирование. Основы Node.js Особенности текстов разных типов
Особенности текстов разных типов Разработка игры по технике безопасности на предприятии (организации)
Разработка игры по технике безопасности на предприятии (организации) Регистрация в Moodle: пошаговая инструкция
Регистрация в Moodle: пошаговая инструкция Способы взаимодействия с онлайн-аудиторией
Способы взаимодействия с онлайн-аудиторией Создание запросов в СУБД Access 2007
Создание запросов в СУБД Access 2007 Разумный подход к ресурсам
Разумный подход к ресурсам Tutoriel pour charger EV avec l’application E-Mobility Développé par SAP
Tutoriel pour charger EV avec l’application E-Mobility Développé par SAP Вычислительные системы, сети и телекоммуникации
Вычислительные системы, сети и телекоммуникации Электронная паспортизация музеев образовательных организаций. Портал Школьные музеи
Электронная паспортизация музеев образовательных организаций. Портал Школьные музеи Классификации ПО. Общие сведения
Классификации ПО. Общие сведения Альбом. Дипломное проектирование
Альбом. Дипломное проектирование Разработка тематического проекта Web-сайта различными инструментами
Разработка тематического проекта Web-сайта различными инструментами Индикаторы качества медицинской помощи. Новая модель премирования работников
Индикаторы качества медицинской помощи. Новая модель премирования работников Темы для самостоятельной работы. Развитие интернет технологий
Темы для самостоятельной работы. Развитие интернет технологий Программы для выполнения (поиск, максимальный и минимальный элементы)
Программы для выполнения (поиск, максимальный и минимальный элементы)