Слайд 4Основные понятия и определения
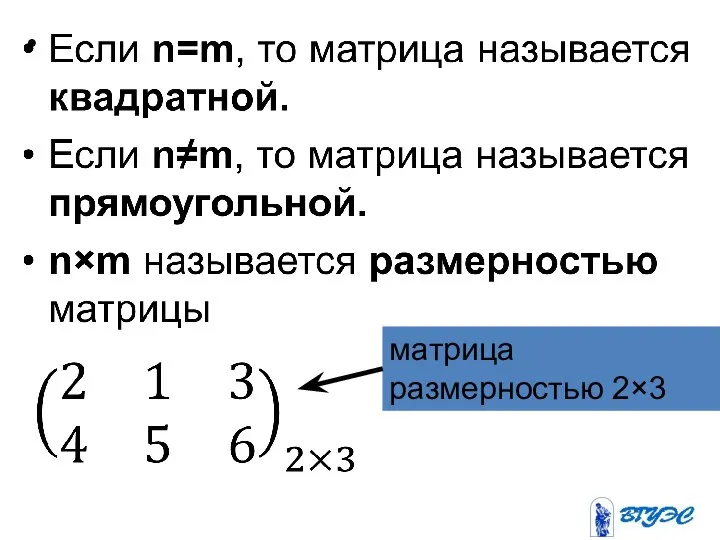
Матрицей называется таблица, состоящая из n строк и m

столбцов.
Таблица имеет вид:
Слайд 6Обозначение матрицы
Матрицы обозначаются заглавными латинскими буквами (A, B, A1, B1) или А={аij}n×m.
Матрица,

у которой все элементы внутри равны 0, называется нулевой матрицей и обозначается «O».
Слайд 9Действия над матрицами
Две матрицы одинаковой размерности называются равными, если равны элементы, стоящие

на одинаковых местах.
Слайд 10Суммой 2-х матриц одинаковой размерности называется матрица, элементы которой находят по правилу:
А={аij}n×m,

B={bij}n×m
A+B=C={cij}n×m.
cij=aij+bij - складываются элементы, стоящие на одинаковых местах.
Слайд 12Для того чтобы матрицу умножить на число, надо каждый элемент матрицы умножить

на это число:
А={аij}n×m; α-число
α∙А={аij}n×m
Слайд 13Если А={аij}n×m, B={bij}n×m, то разностью матриц А и В называется матрица C={cij}n×m,

где cij=aij-bij.
Слайд 14
Введём операцию умножения матрицы таким образом, чтобы выполнялось условие:
Аn×p∙Вp×m=Сn×m.

Слайд 16Свойства операций над матрицами
А+В=В+А
А∙В≠В∙А
α∙(А+В)= αА+ αВ
А(В+С)=А∙В+А∙С (строго!)

Слайд 175) Если в матрице А строки заменить местами, то получим так называемую

транспонированную матрицу.
Если А – матрица, то АТ – транспонированная матрица, тогда (АТ)Т=А; (А∙В)Т=ВТ∙АТ
Слайд 186) Для квадратных матриц вычисляют определители матриц, которые обозначаются символами ΔА; |A|;

||A||; detA (детерминант), являющиеся числом.
det(A∙B)=detA∙detB
Замечание! Все операции определены.
Слайд 19Обратная матрица
Матрица А-1 называется обратной матрице А, если А-1∙А=А∙А-1=Е.
Вывод 1: обратная матрица

существует для квадратной матрицы.
Слайд 21Квадратная матрица, у которой определитель отличен от 0, т.е. |А|≠0, называется невырожденной.

В противном случае называется вырожденной.
Слайд 22Теорема о единственности обратной матрицы.
Если матрица имеет обратную, то единственную.

Слайд 23Теорема о существовании обратной матрицы.
Чтобы матрица имела обратную, необходимо и достаточно, чтобы

она была квадратной и невырожденной.
Необходимость доказательства следует из выводов. Доказательство достаточности представляет собой процесс представления матрицы, которая, по определению, и будет обратной.
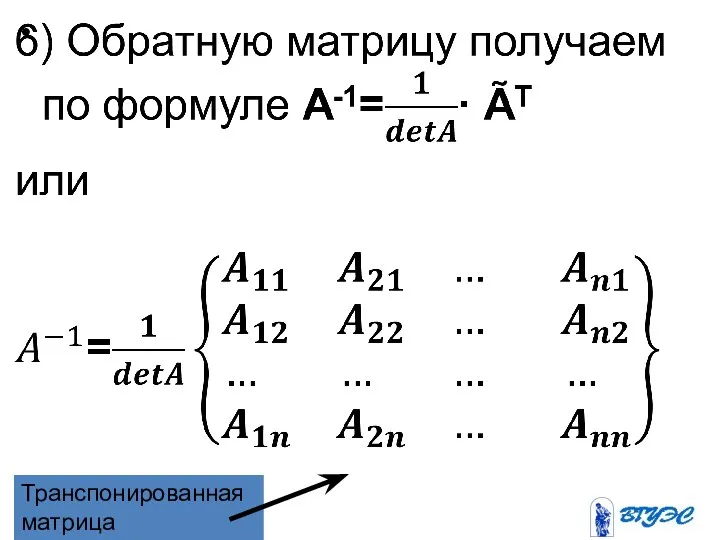
Слайд 24Алгоритм построения обратной матрицы
1) Убеждаемся, что матрица квадратная (для прямоугольных матриц нет

обратных).
2) Вычисляем определитель квадратной матрицы. Если определитель равен 0, то делаем вывод, что у матрицы нет обратной.
Слайд 253) Если определитель не равен 0, то вычисляем алгебраические дополнения элементов матрицы.
4)

Из алгебраических дополнений составляем так называемую присоединённую матрицу (Ã={Aij}n×n).
5) Транспонируем присоединённую матрицу.
Слайд 27Линейная зависимость и линейная независимость столбцов и строк

Слайд 28Столбцы называются линейно-независимыми, когда линейная комбинация равна 0 при всех α=0.
Столбцы называются

линейно-зависимыми, если линейная комбинация равна 0 не при всех α=0.
Слайд 29Теорема.
Столбцы линейно-зависимы, когда хотя бы один столбец является линейной комбинацией остальных.
Теорема.
Столбцы матрицы

можно представить в виде линейной комбинации столбцов матрицы Е.
Слайд 30Ранг матрицы
Дана матрица размером n×m.
Минором порядка r (Mr) называется определитель, составленный из

элементов, стоящих на пересечении любых r строк и любых r столбцов матрицы.
r≤min{n;m}
Слайд 33Минор порядка r называется базисным, если он отличен от 0, и миноры

более высоких порядков равны 0 или не существуют.
Порядок базисного минора называется рангом матрицы (число r).
Слайд 34Нахождение ранга матрицы через миноры трудоёмкая операция. Существует алгоритм, позволяющий достаточно легко

найти ранг и базисный минор.
Слайд 35Теорема.
Ранг матрицы равен максимальному числу линейно-зависимых столбцов матрицы.
Максимальное число линейно-независимых строк равно

максимальному числу линейно-независимых столбцов.
Слайд 36Теорема.
Линейные преобразования столбцов или строк матрицы не меняют ранг матрицы.
К линейным преобразованиям

строк относятся следующие преобразования:
Слайд 37перестановка строк местами;
прибавление к одной строке другой строки, умноженной на некоторое число;
умножение

строки на некоторое число;
те же действия со столбцами.
Слайд 38Теорема.
Ранг матрицы равен числу ненулевых строк (столбцов), полученных в результате применения элементарных

преобразований, которые позволяют выделить строки и столбцы, являющиеся линейными комбинациями других строк (столбцов), т.е. выделить базисный минор.
Слайд 40 Применим к матрице элементарные преобразования.
Подчеркнём элементы, имеющие одинаковые индексы.
Ниже или выше этих

элементов будем получать 0, если понадобится, устраним линейно-зависимые строки.
Слайд 42Вопросы и задания для самопроверки









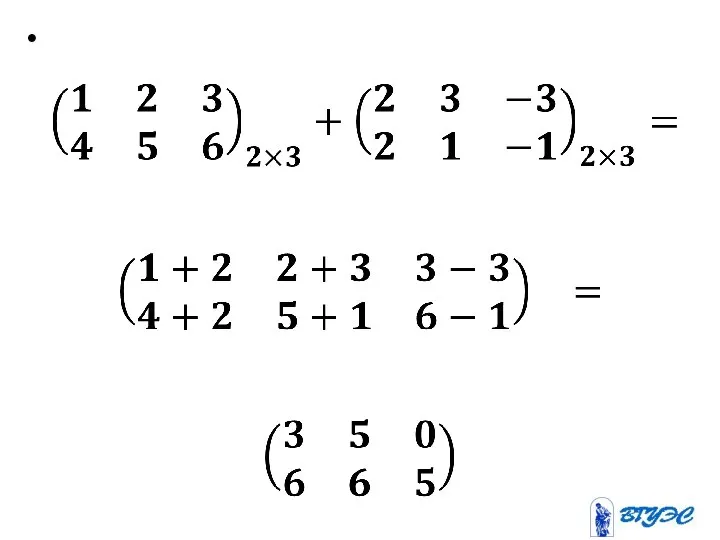



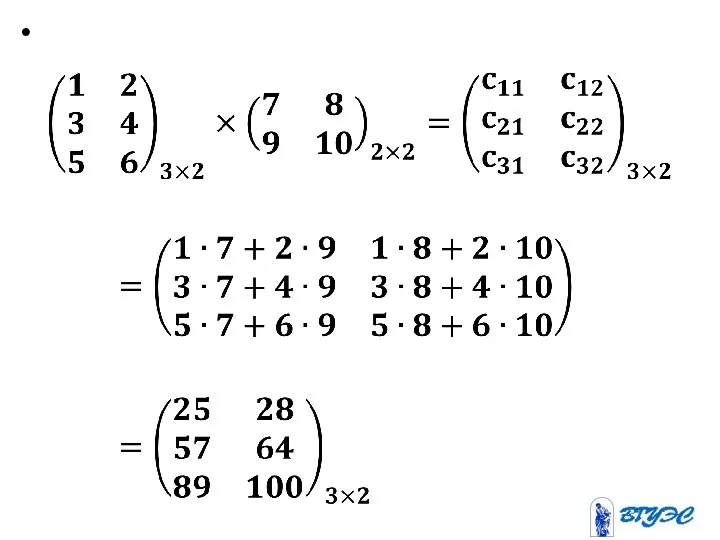



























 Свойства логарифмов
Свойства логарифмов Элементы теории фредгольмовых отображений
Элементы теории фредгольмовых отображений Координатная плоскость
Координатная плоскость Показательные и логарифмические уравнения, системы, неравенства
Показательные и логарифмические уравнения, системы, неравенства Числа 6 и 7. Письмо цифры 7 (1 класс)
Числа 6 и 7. Письмо цифры 7 (1 класс) Справочник по геометрии
Справочник по геометрии Презентация на тему Высказывания со словами: есть, существует, некоторые
Презентация на тему Высказывания со словами: есть, существует, некоторые  Подстановки, оптимизация и решение дифференциальных уравнений (задача Коши)
Подстановки, оптимизация и решение дифференциальных уравнений (задача Коши) Решение задач по теме: Объем цилиндра 11 класс
Решение задач по теме: Объем цилиндра 11 класс Распределительное свойства умножения
Распределительное свойства умножения Общее решение неполного квадратного уравнения. 8 класс
Общее решение неполного квадратного уравнения. 8 класс Задания по геометрии
Задания по геометрии Составление алгоритма
Составление алгоритма Конус
Конус Логарифмические уравнения
Логарифмические уравнения Плоскости
Плоскости Комплексные числа и действия над ними
Комплексные числа и действия над ними Найди значение выражений
Найди значение выражений Размерность. Единицы измерения
Размерность. Единицы измерения Определение вектора
Определение вектора Закрепление изученного. Решение задач
Закрепление изученного. Решение задач Понятие цилиндра
Понятие цилиндра Коэффициент корреляции
Коэффициент корреляции Презентация на тему Деление многозначного числа на однозначное
Презентация на тему Деление многозначного числа на однозначное  Формула полной вероятности и формула Байеса. Формула Бернулли. Лекция 3
Формула полной вероятности и формула Байеса. Формула Бернулли. Лекция 3 Умножение на 2. Проведите динозаврика по лабиринту (2)
Умножение на 2. Проведите динозаврика по лабиринту (2) Прибавление числа 6 с переходом через десяток
Прибавление числа 6 с переходом через десяток Системы степенных неравенств
Системы степенных неравенств