Содержание
- 2. Метод «разделяй и властвуй» ФПМИ БГУ
- 3. «Разделение» Задача разбивается на независимые подзадачи, т.е. подзадачи не пересекаются (две задачи назовем независимыми, если они
- 4. При разбиении задачи на подзадачи полезен принцип балансировки, который предполагает, что задача разбивается на подзадачи приблизительно
- 5. «Разделяй и властвуй» Поиск максимального и минимального элементов Разделим массив на две части (предположим, что n=2k).
- 6. «Разделяй и властвуй» def MergeSort (l,r): if l ≠ r: k = (l + r) //
- 7. «Разделяй и властвуй» def QuickSort(l, r): if l Partition QuickSort(l, j) QuickSort(i, r) Быстрая сортировка массива
- 8. Динамическое программирование ФПМИ БГУ
- 9. Динамическое программирование Динамическое программирование применяется к задачам, в которых нужно что-то подсчитать или к оптимизационным задачам.
- 10. Динамическое программирование Стратегия метода динамического программирования – попытка свести рассматриваемую задачу к более простым задачам. Задача
- 11. Этапы динамического программирования Задача погружается в семейство вспомогательных подзадач той же природы. Возникающие подзадачи могут являться
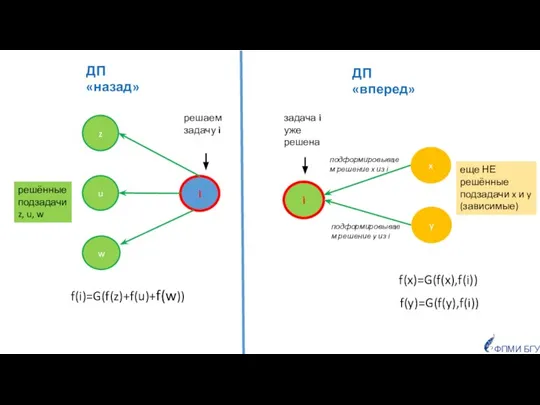
- 12. решаем задачу i i w u z решённые подзадачи z, u, w ДП «назад» f(i)=G(f(z)+f(u)+f(w)) i
- 13. 10 8 не решена 4 2 3 решена 1 5 ФПМИ БГУ 6 9 7 решаем
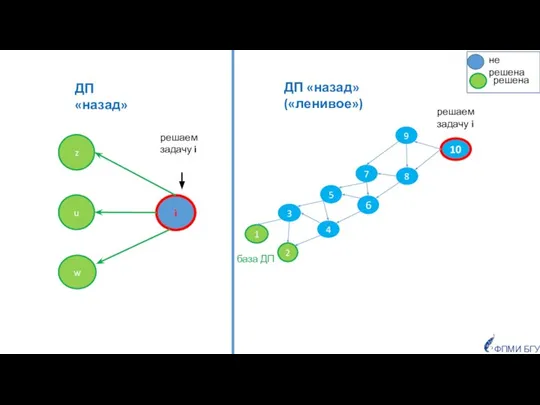
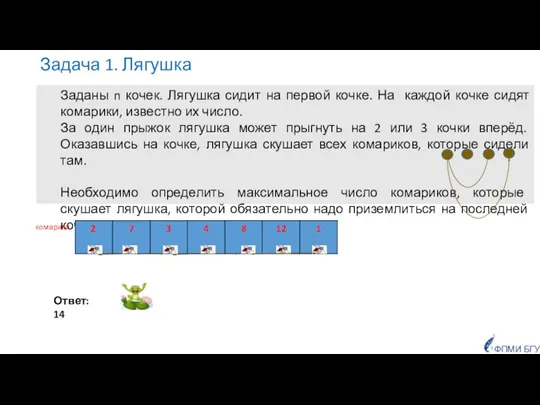
- 14. Задача 1. Лягушка Ответ: 14 Заданы n кочек. Лягушка сидит на первой кочке. На каждой кочке
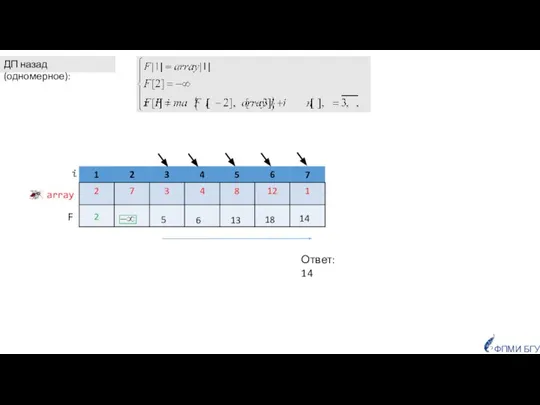
- 15. ДП назад (одномерное): i-1 i-2 i-3 i ФПМИ БГУ
- 16. array i F 2 14 18 13 6 5 ФПМИ БГУ ДП назад (одномерное): Ответ: 14
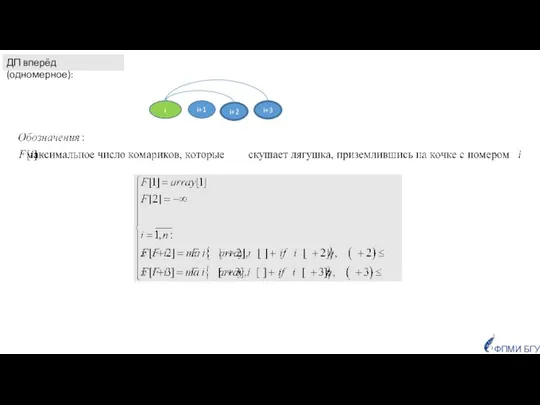
- 17. i+3 i+2 i+1 i ДП вперёд (одномерное): ФПМИ БГУ
- 18. i F 2 7 17 13 6 5 18 14 Время работы алгоритма, основанного на методе
- 19. Полный перебор всех вариантов описывается n-м числом Фибоначчи: Время работы алгоритма для задачи «Лягушка», основанного на
- 20. Задача 2. Задача расстановки единиц Задана строка. Необходимо определить количество способов, для того, чтобы расставить j
- 21. На практике, когда результат является достаточно большим числом, в задаче предлагается найти ответ по модулю (%
- 22. + ФПМИ БГУ
- 23. Обозначим через F[i,j] - количество способов, для того, чтобы расставить j единиц в строке длины i.
- 24. 2 3 3 4 6 4 Время работы алгоритма: ФПМИ БГУ ДП назад (двумерное):
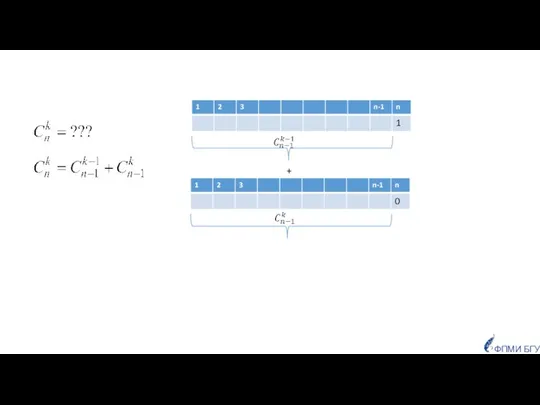
- 25. Обозначим через F[i,j] - количество способов, для того, чтобы расставить j единиц в строке длины i.
- 26. 2 1 1 1 1 1 1 1 1 2 3 3 1 4 3 3
- 27. Задана строка длины n. Необходимо определить количество способов, для того, чтобы расставить j единиц в строке
- 28. Задача 3. Оптимального перемножения группы матриц Порядок перемножения всех s матриц неоднозначен. Чтобы устранить неоднозначность, нужно
- 29. Сведения из математики: при перемножении двух матриц: B [n × k] * C [k × m]
- 30. Числа Каталана – это последовательность чисел, названная в честь бельгийского математика Эжен Шарля Каталана. Сn -
- 31. Рекуррентная и аналитическая формулы для Сn Сn
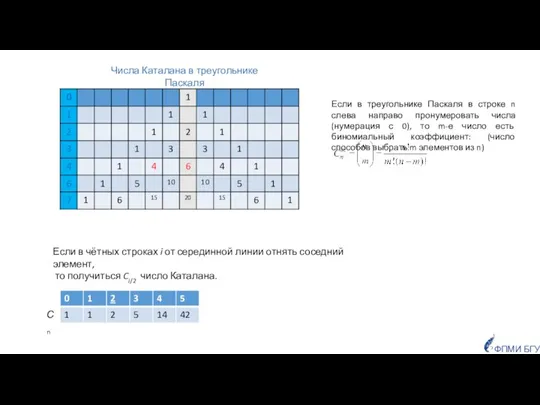
- 32. Числа Каталана в треугольнике Паскаля Если в чётных строках i от серединной линии отнять соседний элемент,
- 33. Количество различных способов задать однозначно порядок перемножения матриц – Сs-1 число Каталана, т.е. экспоненциальная функция. Метод
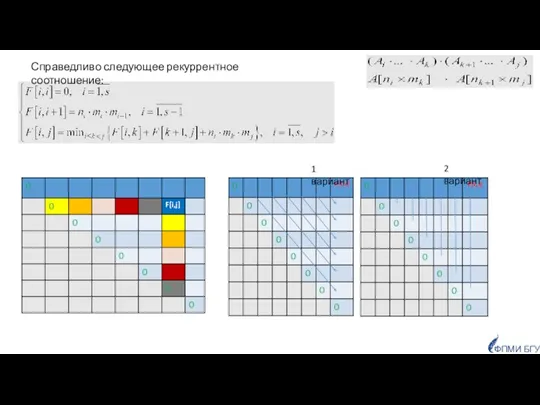
- 34. Обозначим через минимальное число операций умножения, чтобы перемножить матрицы с номерами от i до j включительно:
- 35. Справедливо следующее рекуррентное соотношение: ФПМИ БГУ 1 вариант 2 вариант
- 36. Зависимые подзадачи ФПМИ БГУ
- 37. ФПМИ БГУ
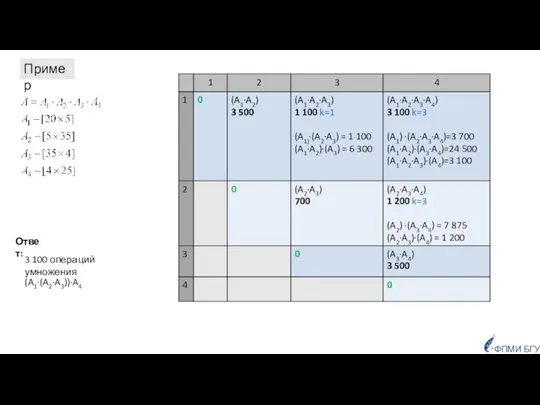
- 38. Время работы алгоритма оптимального перемножения группы матриц, основанного на методе динамического программирования: вычислить s(s+1)/2 элементов таблицы;
- 39. Пример Ответ: (A1·(A2·A3))·A4 3 100 операций умножения ФПМИ БГУ
- 40. Задача 4. Максимальный палиндром Задана строка длины n. Необходимо вычеркнуть минимальное число элементов, чтобы получился палиндром
- 41. Обозначим через F[i,j] длину максимального палиндрома, который можно получить, если мы рассматриваем элементы строки от индекса
- 42. i j i+1 j-1 string Строки длины 1 Строки длины 2 Строки длины >2 ФПМИ БГУ
- 43. Задачи A, B и C являются зависимыми, так как они требуют для своего решения знать длину
- 44. a s d f s l a a s d f s l a a s
- 45. Задания Тема. Динамическое программирование 0.1 Оптимальное перемножение группы матриц (двухмерное ДП) 0.2 Единицы - число сочетаний
- 46. ЗАДАЧА 5. БИНАРНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ ©ФПМИ, БГУ, Доскоч Роман, 2020 год
- 47. ЗАДАЧА Пусть X и Y — две бинарных последовательности длины N и M соответственно, состоящие из
- 48. 1 ЧАСТЬ (НАХОЖДЕНИЕ ДЛИНЫ LCS) Сначала перевернем строки. Дп назад Сложность O(|Y|*|X|) Память O(|Y|*|X|)
- 49. 2 ЧАСТЬ (ВОССТАНОВЛЕНИЕ ПУТИ) i, j текущие индексы i1,j1 индексы первых единиц i0,j0 индексы первых нулей
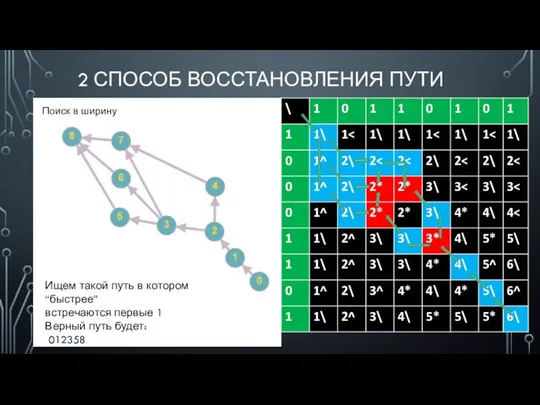
- 50. 2 СПОСОБ ВОССТАНОВЛЕНИЯ ПУТИ Поиск в ширину Ищем такой путь в котором “быстрее” встречаются первые 1
- 52. Скачать презентацию















![Обозначим через F[i,j] - количество способов, для того, чтобы расставить j единиц](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1087116/slide-22.jpg)

![Обозначим через F[i,j] - количество способов, для того, чтобы расставить j единиц](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1087116/slide-24.jpg)



![Сведения из математики: при перемножении двух матриц: B [n × k] *](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1087116/slide-28.jpg)








![Обозначим через F[i,j] длину максимального палиндрома, который можно получить, если мы рассматриваем](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1087116/slide-40.jpg)








 Изучение графического редактора Paint.Net. 7 класс
Изучение графического редактора Paint.Net. 7 класс Социальные сети: предпосылки появления и особенности развития
Социальные сети: предпосылки появления и особенности развития Работа с данными
Работа с данными Базовые алгоритмические конструкции
Базовые алгоритмические конструкции Интернет и всемирная паутина
Интернет и всемирная паутина Санау системасы. БДЭ информатика
Санау системасы. БДЭ информатика Реклама в интернете
Реклама в интернете HASH-функция SHA-1. Лекция 5
HASH-функция SHA-1. Лекция 5 Элементы алгебры логики. Математические основы информатики
Элементы алгебры логики. Математические основы информатики Создание 3D модели на основе операций твердотельного моделирования.(2 занятие)
Создание 3D модели на основе операций твердотельного моделирования.(2 занятие) Вход в АПС Личный кабинет
Вход в АПС Личный кабинет Аргументы приложения Логирование
Аргументы приложения Логирование Системный анализ
Системный анализ Организация проектной и научно-исследовательской деятельности обучающихся на базе лаборатории информатики и ИКТ
Организация проектной и научно-исследовательской деятельности обучающихся на базе лаборатории информатики и ИКТ Ключевые понятия Qlik Sense
Ключевые понятия Qlik Sense Таблицы и картинки в документе Microsoft Word. Урок 9
Таблицы и картинки в документе Microsoft Word. Урок 9 Презентация на тему Компьютерная преступность и безопасность. Компьютерные преступления в Уголовном кодексе РФ
Презентация на тему Компьютерная преступность и безопасность. Компьютерные преступления в Уголовном кодексе РФ  Информационные технологии в экономике
Информационные технологии в экономике Электронные таблицы
Электронные таблицы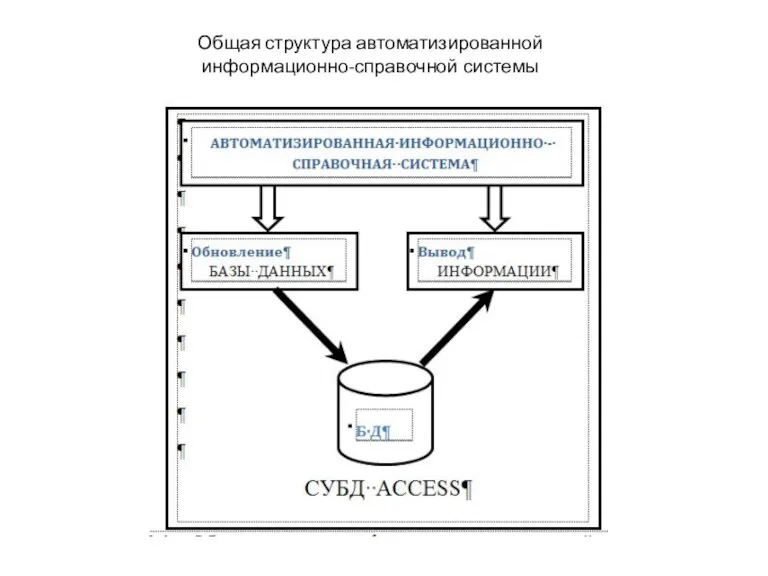 Общая структура автоматизированной информационно-справочной системы
Общая структура автоматизированной информационно-справочной системы Python. Введение
Python. Введение Таблиці в текстових документах
Таблиці в текстових документах Этапы создания сайта на базе платформы simplesite.com
Этапы создания сайта на базе платформы simplesite.com Презентация "Применение фильтров в Photoshop" - скачать презентации по Информатике
Презентация "Применение фильтров в Photoshop" - скачать презентации по Информатике Компьютерные игры
Компьютерные игры Базы данных. Системы управления базами данных (СУБД). MS Access
Базы данных. Системы управления базами данных (СУБД). MS Access Создание гиперссылок
Создание гиперссылок Компьютерные сети
Компьютерные сети