Содержание
- 2. Методы сортировки Сортировку следует понимать как процесс перегруппировки заданного множества объектов в определенном порядке Сортировка применяется
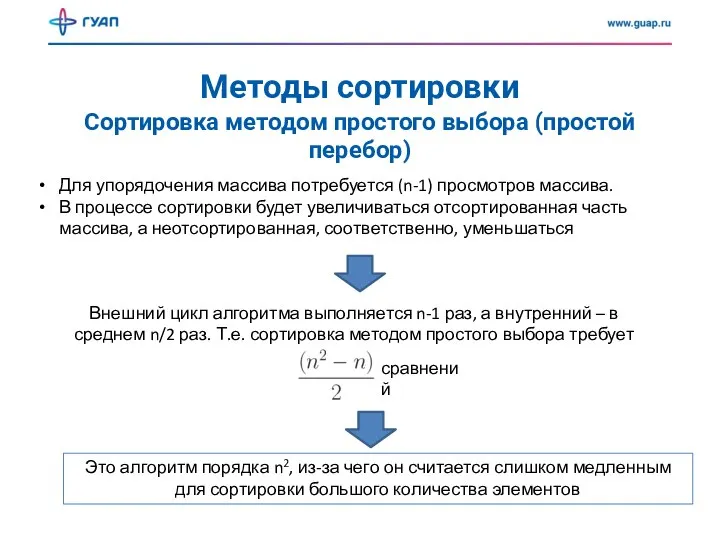
- 3. Методы сортировки Сортировка методом простого выбора (простой перебор) При сортировке массива методом выбора применяется базовый алгоритм
- 4. Методы сортировки Сортировка методом простого выбора (простой перебор) Для упорядочения массива потребуется (n-1) просмотров массива. В
- 5. Методы сортировки Сортировка методом простого выбора (простой перебор) 8 0 -5 4 1 -4 6 -5
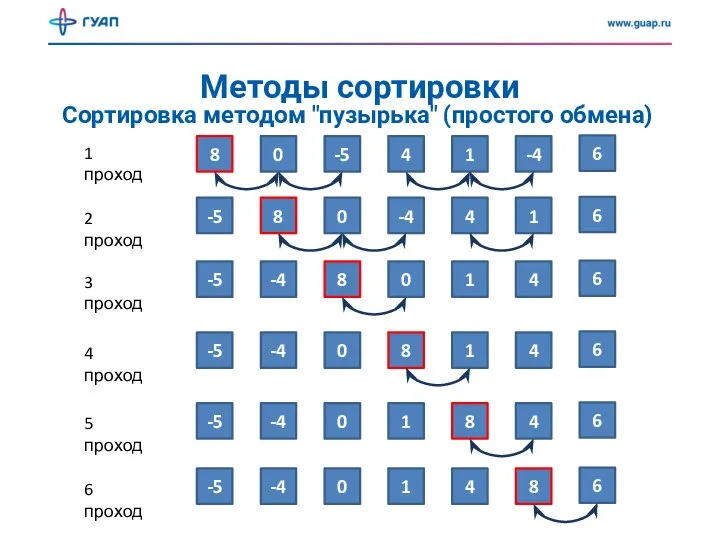
- 6. Методы сортировки Сортировка методом "пузырька" (простого обмена) Алгоритм состоит в повторяющихся проходах по сортируемому массиву. За
- 7. Методы сортировки Сортировка методом "пузырька" (простого обмена) Количество сравнений всегда одно и то же, поскольку два
- 8. Методы сортировки Сортировка методом "пузырька" (простого обмена) 8 0 -5 4 1 -4 6 -5 8
- 9. Методы сортировки Сортировка методом "пузырька" (простого обмена) Особенность: неупорядоченные элементы на "большом" конце массива занимают правильные
- 10. Методы сортировки Шейкер-сортировка Массив просматривается поочередно справа налево и слева направо. Просмотр массива осуществляется до тех
- 11. Методы сортировки Сортировка пузырьком - вариант с "флагом" Если при выполнении прохода методом пузырька не было
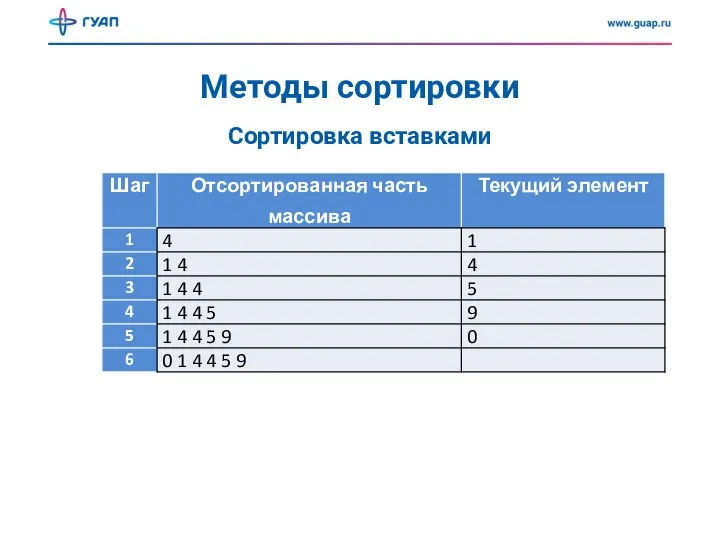
- 12. Методы сортировки Сортировка вставками В начале сортировки первый элемент массива считается отсортированным, все остальные — не
- 13. Методы сортировки Сортировка вставками
- 14. Методы сортировки Метод Шелла Метод построен на основе метода вставки с минимизацией промежуточных шагов. Общая схема
- 15. Методы сортировки Метод Шелла Исходный массив чисел Шаг 1. 10/2 = 5. Числа расположены на расстоянии
- 16. Методы сортировки Метод Шелла Шаг 2. 5/2=2. Числа расположены на расстоянии 2 друг от друга. Отсортируем
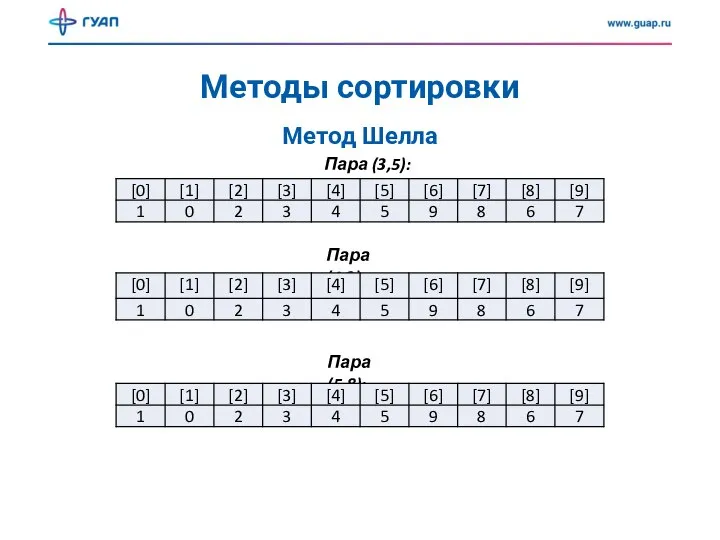
- 17. Методы сортировки Метод Шелла Пара (3,5): Пара (4,9): Пара (5,8):
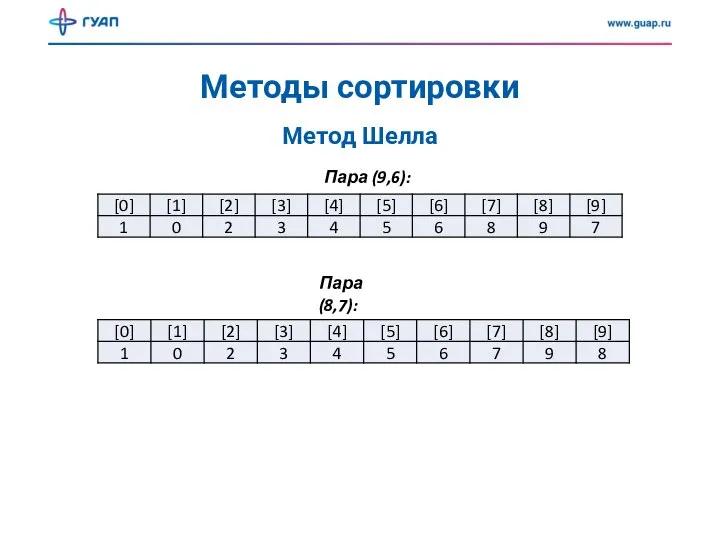
- 18. Методы сортировки Метод Шелла Пара (9,6): Пара (8,7):
- 19. Методы сортировки Метод Шелла Шаг 3. 2/2 = 1. Числа расположены на расстоянии 1 друг от
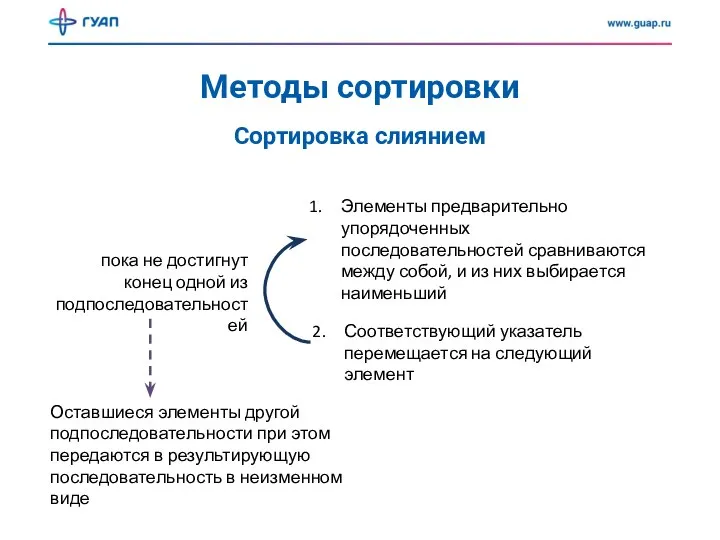
- 20. Методы сортировки Сортировка слиянием Слияние означает объединение двух (или более) последовательностей в одну упорядоченную последовательность при
- 21. Методы сортировки Сортировка слиянием Элементы предварительно упорядоченных последовательностей сравниваются между собой, и из них выбирается наименьший
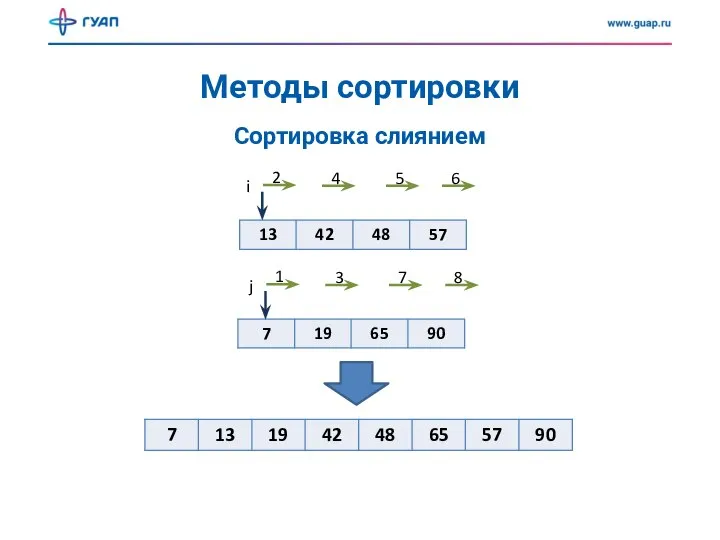
- 22. Методы сортировки Сортировка слиянием i 2 4 5 6 j 1 3 7 8
- 23. Методы сортировки Сортировка слиянием Алгоритм двухпутевого слияния (1/3) Исходная последовательность разбивается на две подпоследовательности Эти две
- 24. Методы сортировки Сортировка слиянием Полученная последовательность снова разбивается на две, и пары объединяются в упорядоченные четверки
- 25. Методы сортировки Сортировка слиянием Полученная последовательность снова разбивается на две и собирается в упорядоченную восьмерку Операция
- 26. Методы сортировки Сортировка слиянием Метод нисходящего слияния (1/2) Исходная последовательность рекурсивно разбивается на половины, пока не
- 27. Методы сортировки Сортировка слиянием Метод нисходящего слияния (2/2) Каждую подпоследовательность упорядочиваем методом слияния и получаем готовую
- 28. Методы сортировки Сортировка слиянием Метод восходящего слияния Исходная последовательность представляется как последовательный набор отдельных элементов
- 29. Методы сортировки Рекурсия Решение той или иной задачи может быть выражено как комбинация или модификация решений
- 30. Методы сортировки Рекурсия Пример Задача о числе разбиений Найти число способов, каким можно разбить целое положительное
- 31. Методы сортировки Рекурсия Пример Все возможные разбиения числа 6: 6=6, 6 = 5+1, 6 = 4+2,
- 32. Методы сортировки Рекурсия Пример P(N) - количество разбиений числа N число разбиений можно сводить к числу
- 33. Методы сортировки Рекурсия Пример Пусть имеем какое-то разбиение и в нем максимальное слагаемое M, т.е. ni
- 34. Методы сортировки Рекурсия Пример Тогда P(N) может быть выражено как P(N)=Q(N,N) На первом шаге всегда можно
- 35. Методы сортировки Рекурсия Пример Применим полученные рекурсивные выражения для вычисления P(6) P(6) = Q(6,6) = 1+Q(6,5)(в
- 36. Методы сортировки Метод Хоара для упорядочивания массива Быстрая сортировка представляет собой усовершенствованный метод сортировки, основанный на
- 37. Методы сортировки Метод Хоара для упорядочивания массива Тем самым массив разбивается на две части не отсортированные
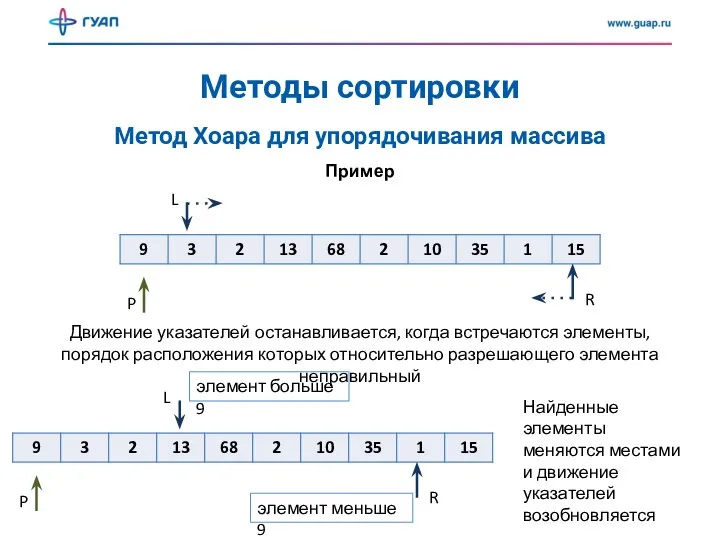
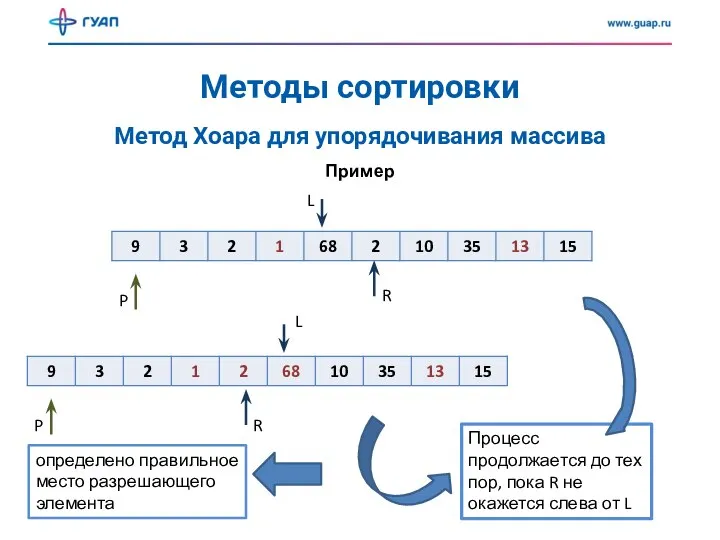
- 38. Методы сортировки Метод Хоара для упорядочивания массива Пример L R P Движение указателей останавливается, когда встречаются
- 39. Методы сортировки Метод Хоара для упорядочивания массива Пример L R P L R P Процесс продолжается
- 41. Скачать презентацию





























 Информационные процессы в системах
Информационные процессы в системах Оформление текста
Оформление текста Професия Разработчик
Професия Разработчик Базы данных. Access 2007. Макросы
Базы данных. Access 2007. Макросы Introduction Dr. Suad El-Geder
Introduction Dr. Suad El-Geder Dzień dobry, proszę o wykonanie polecenia z opisu, na tej podstawie otrzymają
Dzień dobry, proszę o wykonanie polecenia z opisu, na tej podstawie otrzymają Prezentācija par vīrusiem un antivīrusu programmām
Prezentācija par vīrusiem un antivīrusu programmām Иллюстратор - соавтор писателя
Иллюстратор - соавтор писателя Логика. Подготовка к ГИА по информатике
Логика. Подготовка к ГИА по информатике Обеспечение качества аэронавигационных данных
Обеспечение качества аэронавигационных данных Интернет и социальные сети в электоральных процессах
Интернет и социальные сети в электоральных процессах Программирование на языке C++
Программирование на языке C++ Компьютерная графика
Компьютерная графика Презентация "Алгоритмы и типы алгоритмов" - скачать презентации по Информатике
Презентация "Алгоритмы и типы алгоритмов" - скачать презентации по Информатике Оптические кабели
Оптические кабели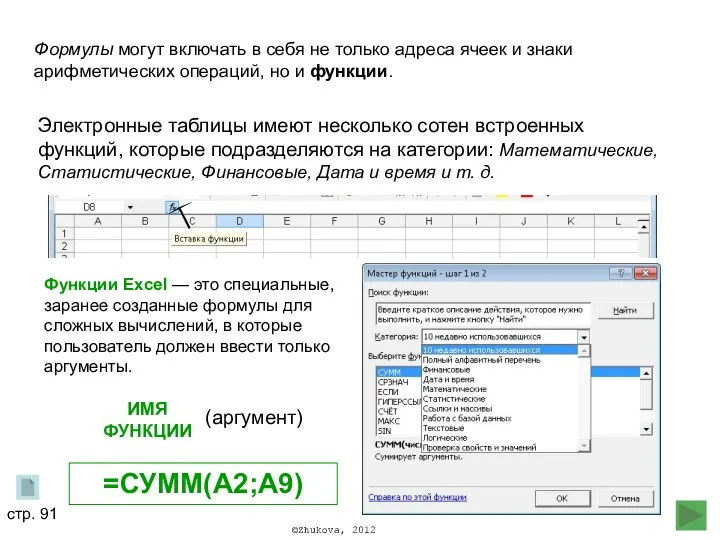 Электронные таблицы
Электронные таблицы Решение систем уравнений графическим способом
Решение систем уравнений графическим способом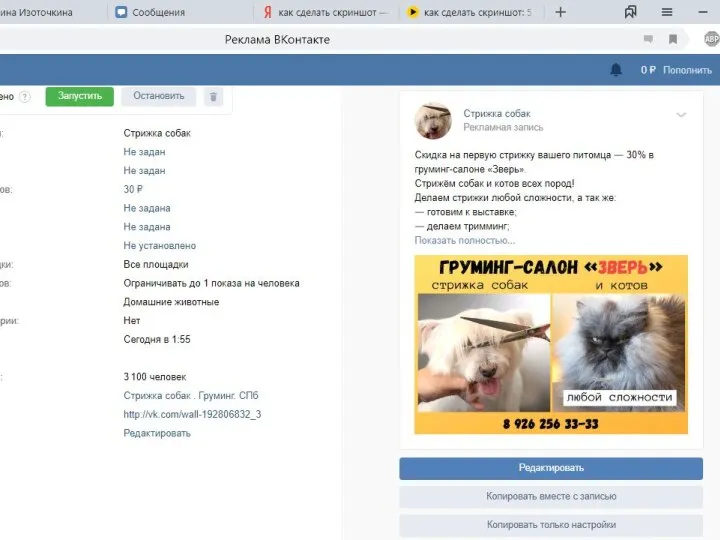 Груминг-салон Зверь
Груминг-салон Зверь Леттеринг и его применение
Леттеринг и его применение Базы данных. § 12. Информационные системы
Базы данных. § 12. Информационные системы Проверка орфографии
Проверка орфографии Управление росреестра по Свердловской области
Управление росреестра по Свердловской области Operation Stratis
Operation Stratis Обзор технологий интеллектуализации ГИС
Обзор технологий интеллектуализации ГИС Про TypeScript и про нас
Про TypeScript и про нас Решение задачи О рюкзаке методом динамического программирования
Решение задачи О рюкзаке методом динамического программирования Вред и польза компьютерных игр
Вред и польза компьютерных игр Конкурсные механики
Конкурсные механики