Свойства логических высказываний

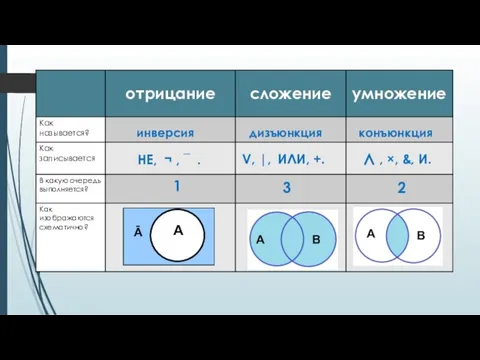
повторение
инверсия
дизъюнкция
конъюнкция
∧ , ×, &, И.
V, |, ИЛИ, +.
НЕ, ¬ , ¯ .
1
3
2
A
Ā
A
B
A
B

Для построения таблицы истинности следует:
Подсчитать n — число переменных в выражении.
Подсчитать общее число логических операций в выражении.
Установить последовательность выполнения логических операций с учётом скобок и приоритетов;
Определить число столбцов в таблице: число переменных + число операций.
Заполнить шапку таблицы, включив в нее все переменные и операции в соответствии с последовательностью.
Определить число строк в таблице (не считая шапку таблицы)

Составляем таблицу истинности
2
1
2
3
4
0 0
0 1
1 0
1 1
1
1
0
0
0
1
1
1
1
1
0
1
0
1
0
1

Построить таблицу истинности для
1. A ˄ (B ˅ В ˄ С)
2. (X1&X2) ˅ ( X1˅X2)

Что можно сказать о свойствах алгебраических и логических выражений?

Что можно сказать о свойствах алгебраических и логических выражений?

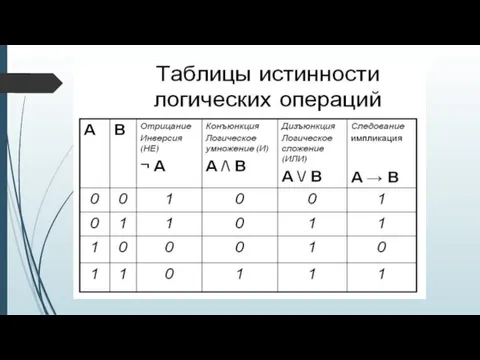
Свойства логических операций

Для любых логических формул A, B, C истинны следующие неравенства
1. Закон двойного отрицания
¬¬A=A
Двойное отрицание исключает отрицание.

Для любых логических формул A, B, C истинны следующие неравенства
2. Закон повторения
- для логического умножения
A & A = A
- для логического сложения
A v A = A

Для любых логических формул A, B, C истинны следующие неравенства
3. Коммутативный (переместительный) закон
- для логического умножения
A & B = B & A
- для логического сложения
A v B = B v A

Для любых логических формул A, B, C истинны следующие неравенства
4. Ассоциативный (сочетательный) закон
- для логического умножения
(A & B) & C = A & (B & C)
- для логического сложения
(A v B) v C = A v (B v C)

Для любых логических формул A, B, C истинны следующие неравенства
5. Дистрибутивный (распределительный) закон
- для логического умножения
A & (B v C) = (A & B) v (A & C)
- для логического сложения
A v (B & C) = (A v B) & (A v C)

Для любых логических формул A, B, C истинны следующие неравенства
6. Законы поглощения
- для логического умножения
A & (A v C) = A
- для логического сложения
A v (A & C) = A

Для любых логических формул A, B, C истинны следующие неравенства
7. Законы общей инверсии (законы де Моргана)
- для логического умножения
¬(A & B) = ¬A v ¬B
- для логического сложения
¬(A v C) = ¬A & ¬B

Для любых логических формул A, B, C истинны следующие неравенства
8. Законы исключения третьего
- для логического умножения
A & ¬A = 0
- для логического сложения
A v ¬A = 1

Для любых логических формул A, B, C истинны следующие неравенства
9. Законы операций с 0 и 1
- для логического умножения
A & 0 = 0; A & 1 = A
- для логического сложения
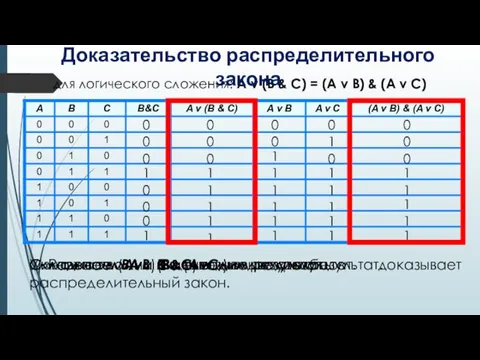
A v 0 = A; A v 1 = 1

для логического сложения: A v (B & C) = (A v B) & (A v C)
Доказательство распределительного закона
Умножаем В на С и выводим результат.
0
0
0
0
0
0
1
1
Складываем А и В и выводим результат.
0
0
0
1
1
1
1
1
Складываем А и (В&С) и выводим результат.
0
0
1
1
1
1
1
1
Складываем А и C и выводим результат.
0
0
1
1
1
1
1
1
Умножаем (АvB) на (AvC )и выводим результат.
0
0
0
1
1
1
1
1
Равенство выделенных столбцов доказывает распределительный закон.