Содержание
- 2. Ключевые слова Схема Граф Сеть Дерево
- 3. Схема - это представление объекта в общих, главных чертах с помощью условных обозначений. Схема радиоприёмника Многообразие
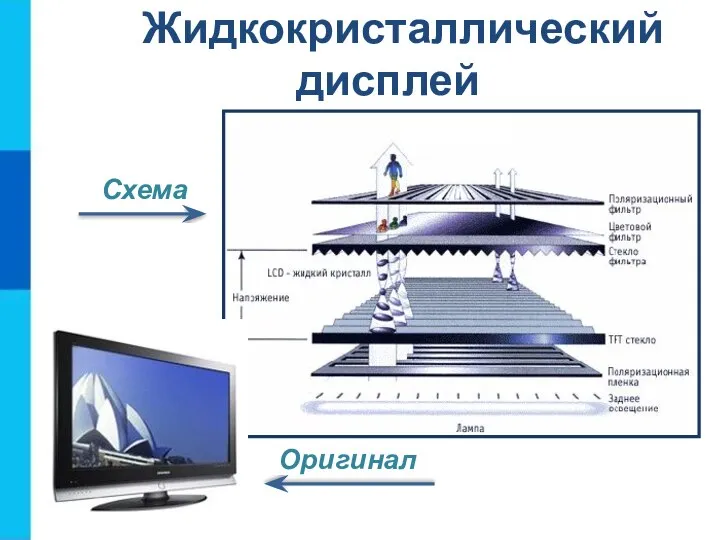
- 4. Жидкокристаллический дисплей Схема Оригинал
- 5. Схема зала театра им. Вахтангова
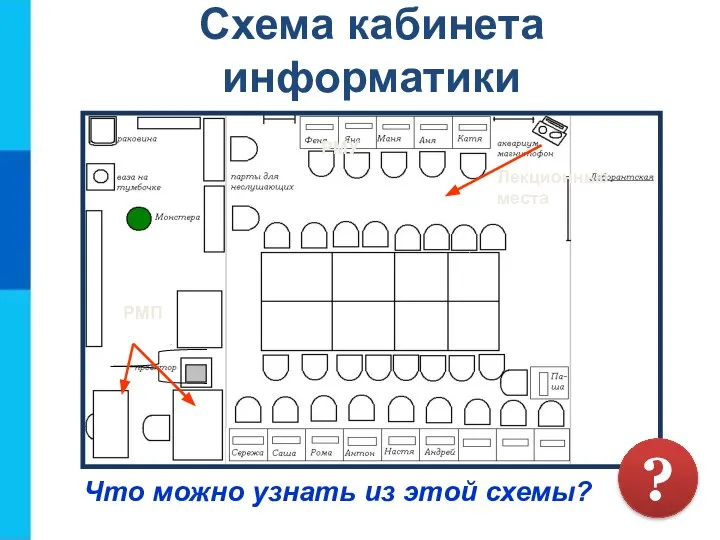
- 6. Схема кабинета информатики Что можно узнать из этой схемы? Лекционные места РМУ РМП ?
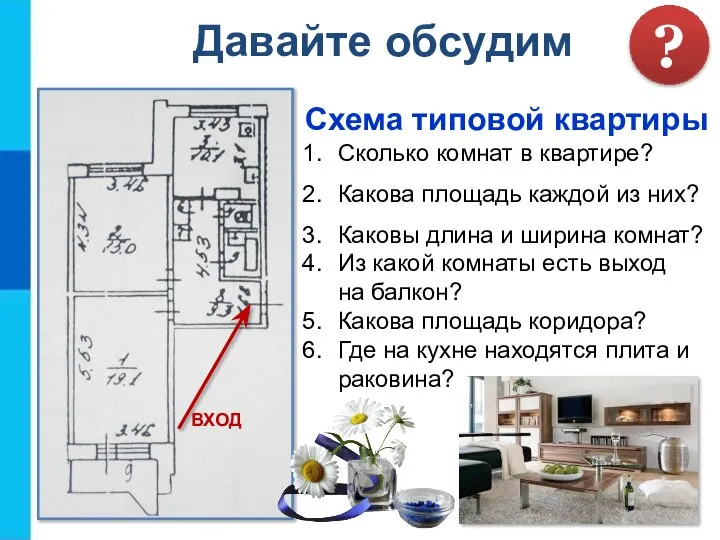
- 7. Схема типовой квартиры ВХОД Сколько комнат в квартире? Какова площадь каждой из них? Каковы длина и
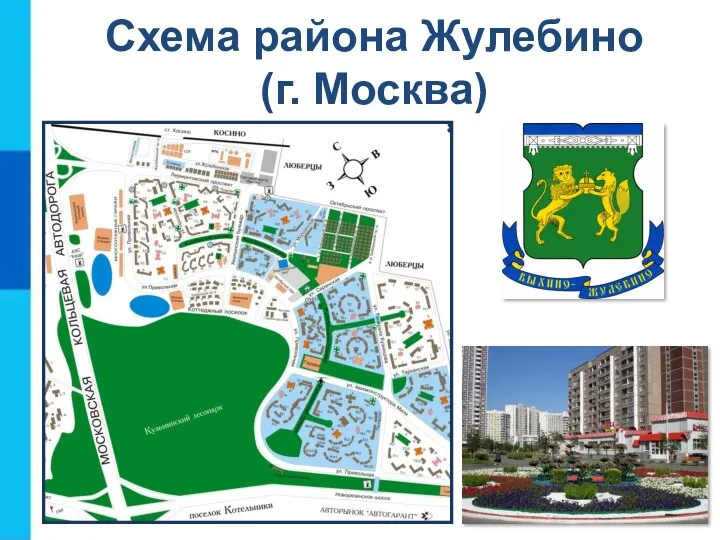
- 8. Схема района Жулебино (г. Москва)
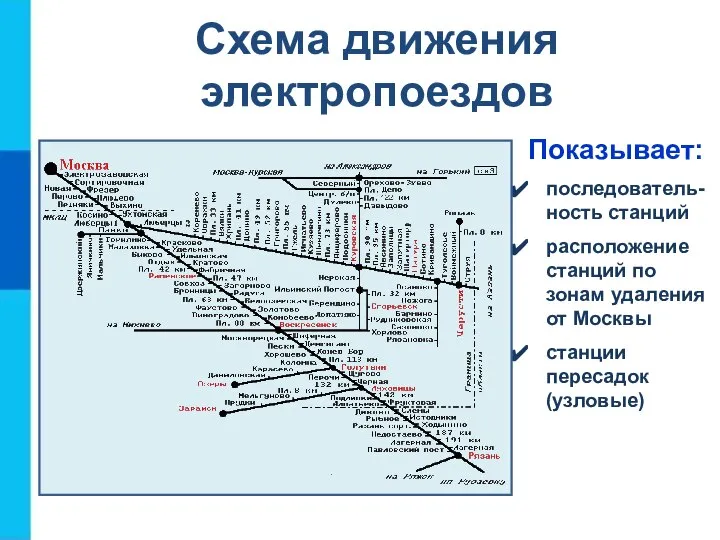
- 9. Схема движения электропоездов Показывает: последователь-ность станций расположение станций по зонам удаления от Москвы станции пересадок (узловые)
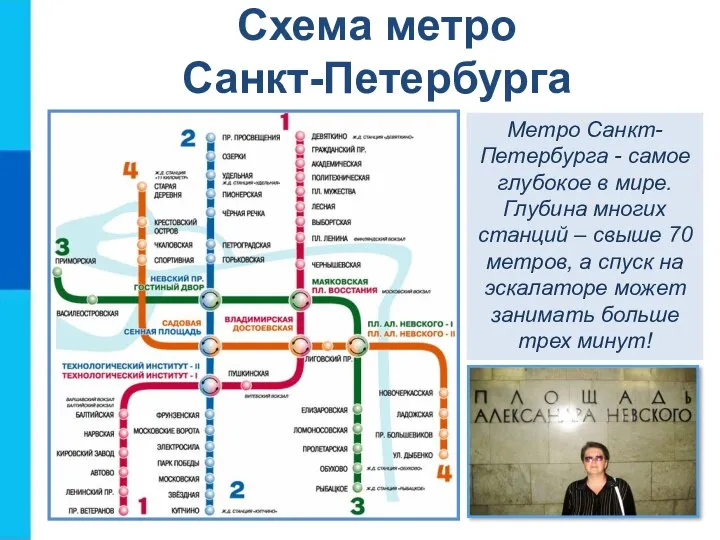
- 10. Схема метро Санкт-Петербурга Метро Санкт-Петербурга - самое глубокое в мире. Глубина многих станций – свыше 70
- 11. Карта центра Санкт-Петербурга Покажите досто- примечательности, представленные на карте. ?
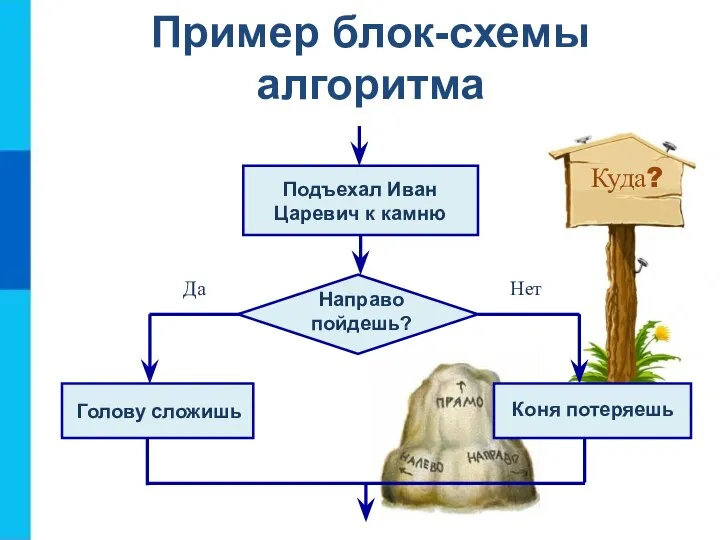
- 12. Пример блок-схемы алгоритма
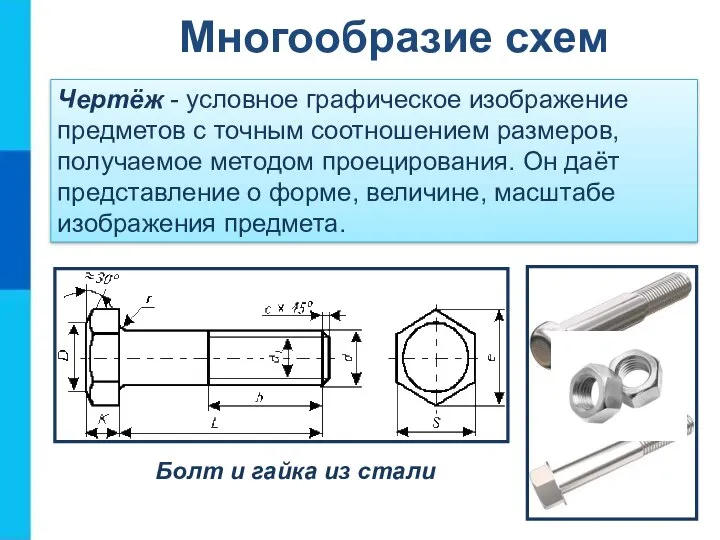
- 13. Чертёж - условное графическое изображение предметов с точным соотношением размеров, получаемое методом проецирования. Он даёт представление
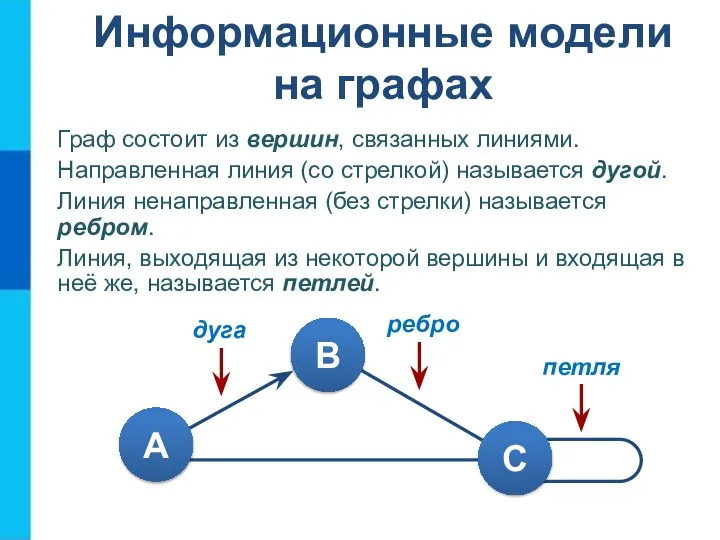
- 14. Информационные модели на графах Граф состоит из вершин, связанных линиями. Направленная линия (со стрелкой) называется дугой.
- 15. Изображение вершин графа
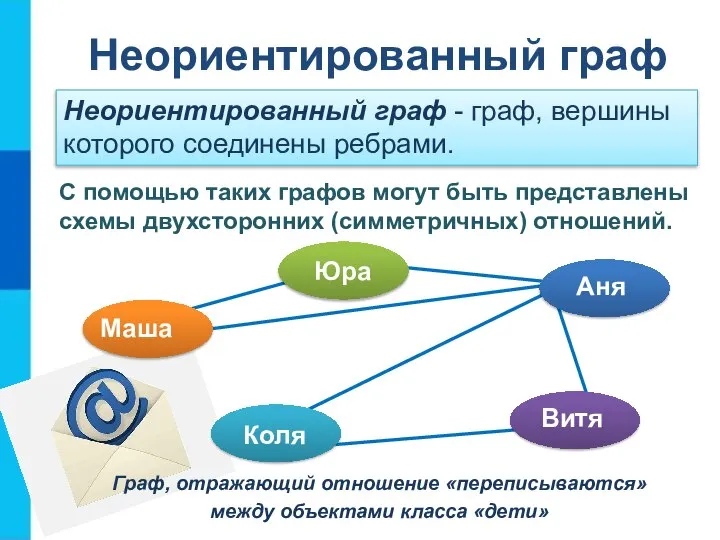
- 16. Неориентированный граф С помощью таких графов могут быть представлены схемы двухсторонних (симметричных) отношений. Граф, отражающий отношение
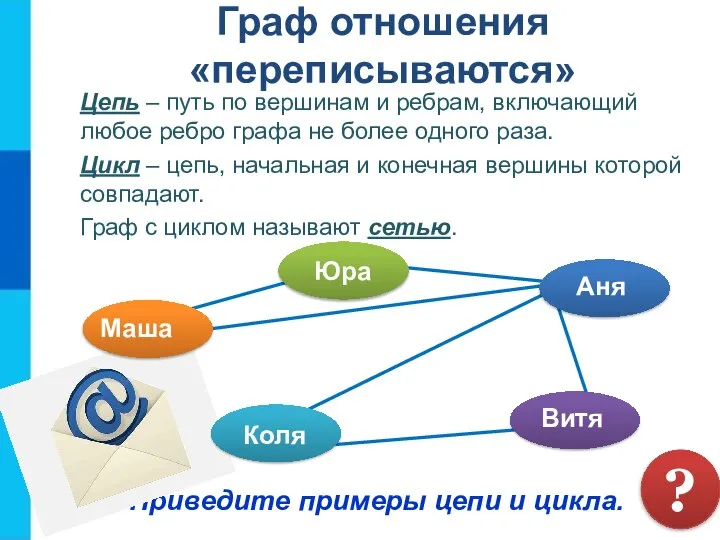
- 17. Граф отношения «переписываются» Цепь – путь по вершинам и ребрам, включающий любое ребро графа не более
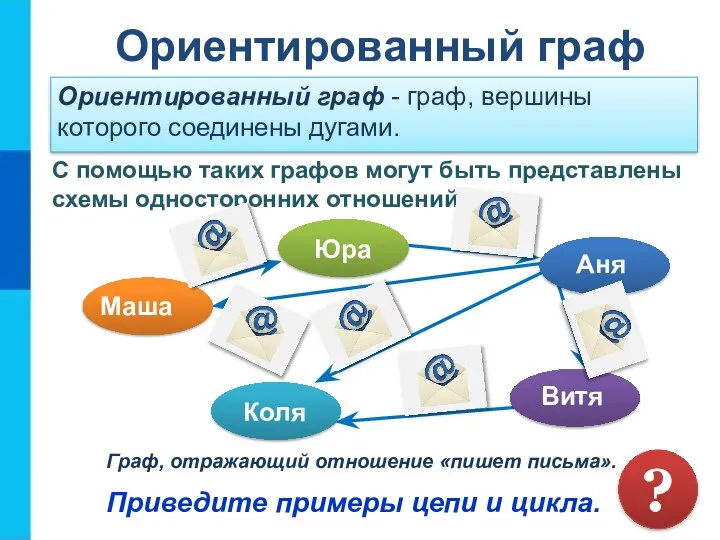
- 18. Ориентированный граф Ориентированный граф - граф, вершины которого соединены дугами. Граф, отражающий отношение «пишет письма». Приведите
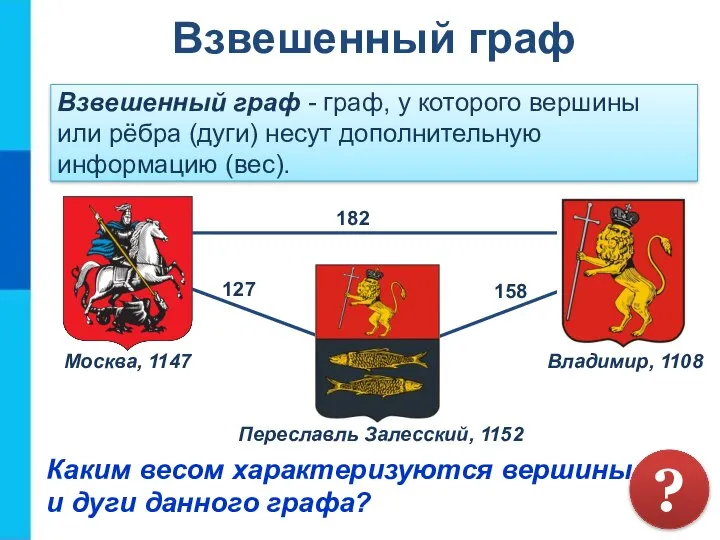
- 19. Взвешенный граф - граф, у которого вершины или рёбра (дуги) несут дополнительную информацию (вес). Каким весом
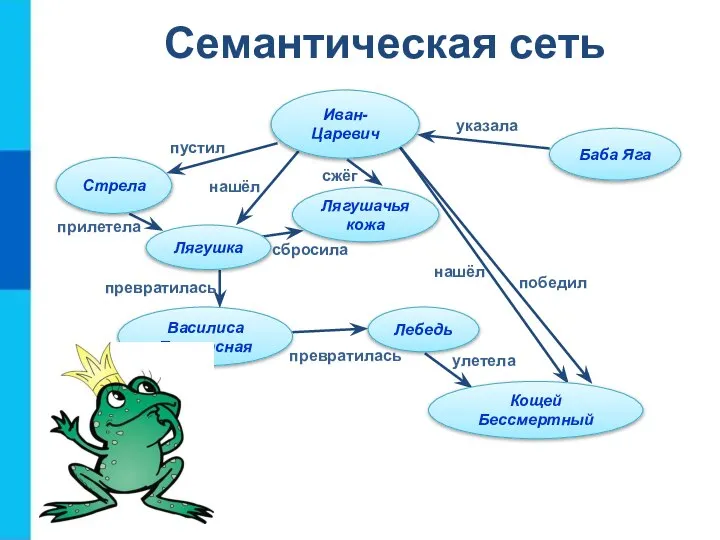
- 20. Семантическая сеть
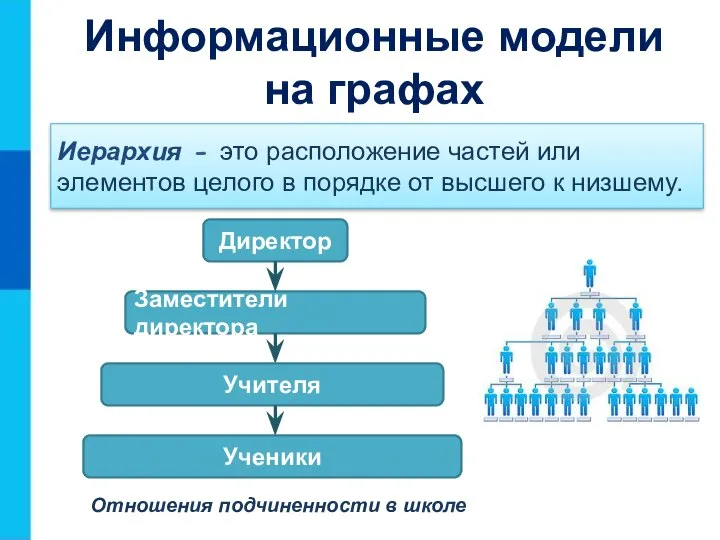
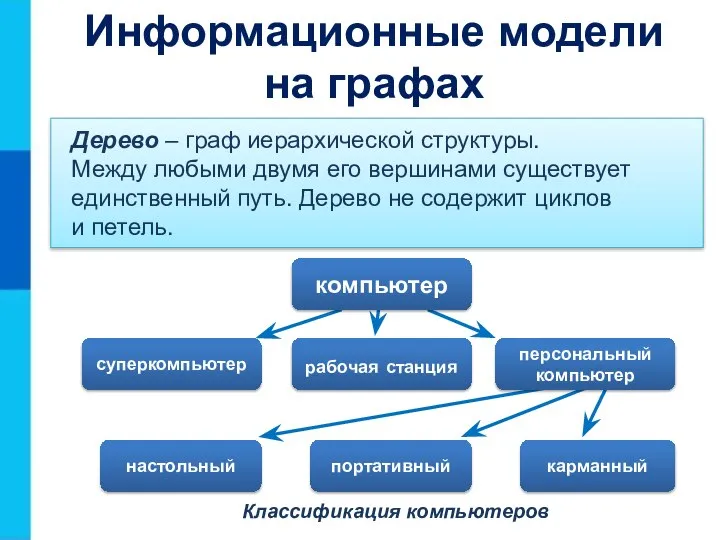
- 21. Информационные модели на графах Иерархия - это расположение частей или элементов целого в порядке от высшего
- 22. Классификация компьютеров Дерево – граф иерархической структуры. Между любыми двумя его вершинами существует единственный путь. Дерево
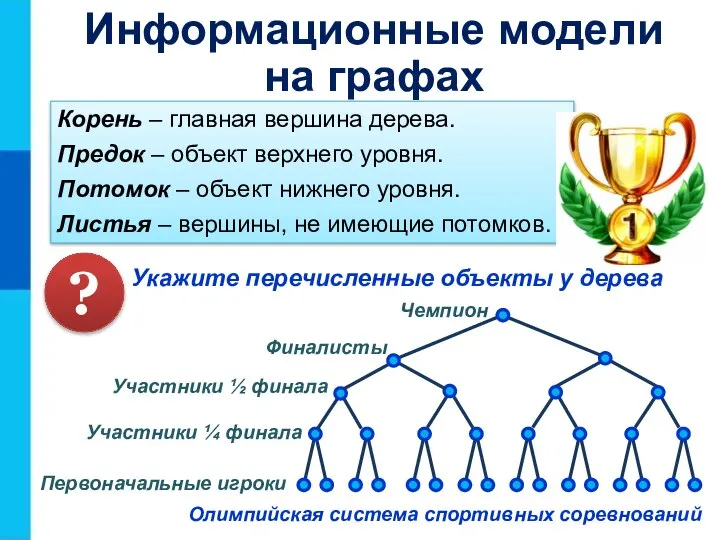
- 23. Чемпион Финалисты Участники ½ финала Участники ¼ финала Первоначальные игроки Укажите перечисленные объекты у дерева Корень
- 24. Файловая структура Укажите корневую вершину, объекты 1-го, 2-го и 3-го уровней. ?
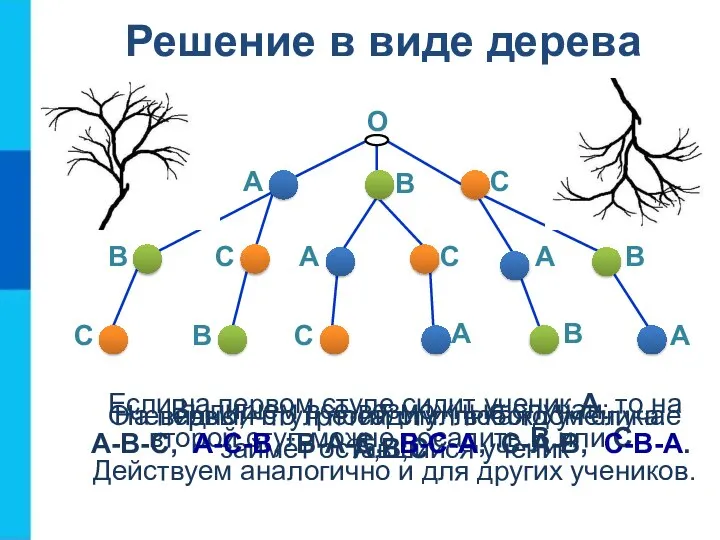
- 25. Графы при решении задач Сколькими способами можно рассадить в ряд на три стула трёх учеников? Выписать
- 26. Решение в виде дерева О На первый стул посадим любого ученика: А,В,С Если на первом стуле
- 28. Скачать презентацию






 Выживание человека и формирование личности в условиях агрессивной антипедагогической информационной среды: современные вызовы
Выживание человека и формирование личности в условиях агрессивной антипедагогической информационной среды: современные вызовы Расчет микросборки (микровыключателя)
Расчет микросборки (микровыключателя) Симметричное и ассиметричное шифрование
Симметричное и ассиметричное шифрование 10-05-Кодирование текстовой информации (1)
10-05-Кодирование текстовой информации (1) Библиографическая запись. Библиографическое описание
Библиографическая запись. Библиографическое описание Электронные таблицы. 9 класс
Электронные таблицы. 9 класс Безопасность в Интернете
Безопасность в Интернете Безопасное и рациональное использование личных и персональных данных в интернет-пространстве. Занятие 6
Безопасное и рациональное использование личных и персональных данных в интернет-пространстве. Занятие 6 Книжный обзор. Старая стратегия с новыми вводными
Книжный обзор. Старая стратегия с новыми вводными Моделирование течений вязкой несжимаемой жидкости в системах конечно-элементного анализа
Моделирование течений вязкой несжимаемой жидкости в системах конечно-элементного анализа Space Calendar Randomiser
Space Calendar Randomiser Дискретное представление информации
Дискретное представление информации Мои улучшения в играх
Мои улучшения в играх Графические редакторы: назначение и основные возможности
Графические редакторы: назначение и основные возможности Агрегирование каналов
Агрегирование каналов Открытая архитектура и экосистема RISC-V
Открытая архитектура и экосистема RISC-V Контент для каждого. Мастер-класс для участников экспресс-курса Основы SMM
Контент для каждого. Мастер-класс для участников экспресс-курса Основы SMM Библиотека в социальных сетях
Библиотека в социальных сетях Глобальная сеть Internet
Глобальная сеть Internet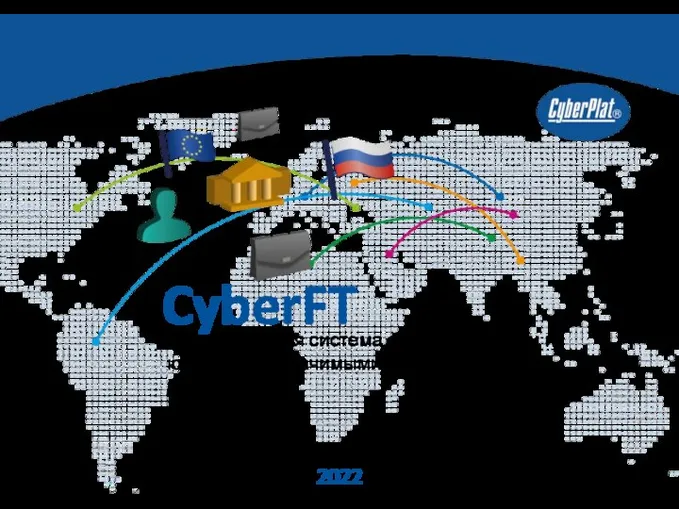 Универсальная система обмена данными и юридически значимыми электронными документами 2022
Универсальная система обмена данными и юридически значимыми электронными документами 2022 Создание базы данных
Создание базы данных Интеллектуальные фильтры Доклад по проекту предмета «Управление знаниями» подготовил студент 5-го курса ОД-5 Воронин Э. Ф.
Интеллектуальные фильтры Доклад по проекту предмета «Управление знаниями» подготовил студент 5-го курса ОД-5 Воронин Э. Ф. Системы автоматического обзвона и самозаписи пациентов на прием в клинику АО Медицина
Системы автоматического обзвона и самозаписи пациентов на прием в клинику АО Медицина Создание 2D персонажа. Ведьмочка
Создание 2D персонажа. Ведьмочка Информационные технологии в индустрии полимеров. Практическое занятие 2
Информационные технологии в индустрии полимеров. Практическое занятие 2 CNews Forum
CNews Forum Знакомимся с компьютером (технология). 3 класс
Знакомимся с компьютером (технология). 3 класс Разработка базы данных по учету и потовой продаже запасных частей к холодильному оборудованию
Разработка базы данных по учету и потовой продаже запасных частей к холодильному оборудованию