Слайд 3Проблема missing data
В любом исследовании неизбежно часть данных, которые планировалось собрать, не

будут собраны
Пациенты выбывают из исследования, пропускают визиты, аппаратура дает сбои и проч.
Как минимум отсутствующие данные уменьшают мощность статистических тестов (меньше пациентов)
Как максимум могут привести к неверным выводам
Слайд 4Проблема missing data
Рассмотрим исследование средства для снижения веса
100 участников принимают его в

течение года
На самом деле средство вообще не работает
Но в течение года часть участников по независимым причинам худеет, а часть толстеет
Те, кто толстеют, выбывают из исследования, но те, кто худеют, думают, что средство действует и остаются
Слайд 5Проблема missing data
В конце исследования у нас есть данные только тех, кто

похудел. Если судить по ним, получается, что средство отлично работает
Но это ошибка, потому что мы не учли отсутствующие данные
Слайд 6Missing Mechanisms
Missing Completely at Random (MCAR): вероятность, что у конкретного пациента будет

missing значение не зависит от пациента
Missing at Random (MAR): вероятность, что у конкретного пациента будет missing значение может зависеть от наблюдаемых факторов (treatment group, baseline characteristic)
Missing Not at Random (MNAR): вероятность, что у конкретного пациента будет missing значение может зависеть от ненаблюдаемых факторов, например самого missing значения
Слайд 7Missing Mechanisms
Пример со средством для снижения веса – MNAR
MCAR и MAR –

не очень большая проблема
MNAR – большая проблема
Дополнительная проблема, что невозможно отличить MAR от MNAR по имеющимся данным. Отличие как раз в тех данных, которых нет.
Вначале мы рассмотрим ситуацию MAR. MNAR рассмотрим отдельно в конце.
Слайд 8Imputation Methods
Большое разнообразие: LOCF, worst case, среднее по группе и проч.
Multiple Imputation

– надежный метод, хорошо работающий в широком спектре практических задач
Правда, немного сложный. Но сегодня мы с ним разберемся
Слайд 9План семинара
Основы теории
Реализация метода MI в SAS: процедуры MI и MIANALYZE
MI и

ADaM-датасеты
Проверка предположений MAR/MNAR
Слайд 10MULTIPLE IMPUTATIONS – ОСНОВЫ ТЕОРИИ

Слайд 11Идея multiple imputation
Основная идея – давайте построим модель для предсказания отсутствующих данных
Мы

же строим статистические модели на данных, собранных в исследовании, чтобы предсказать, как лекарство подействует на других пациентов в будущем
Так давайте построим модель на тех пациентах, у которых есть полные данные и предскажем missing результаты
Слайд 12Пример моделирования
Пример: допустим мы измеряем рост пациентов, и у нескольких рост не

был измерен
Построим простую модель с одним фактором «пол» для предсказания роста
Слайд 14Проблема простого моделирования
Хорошая идея, но вот проблема. Imputed рост будет использован затем

в каком-то анализе, например ANOVA модель, в которой рост – один из факторов
Но ведь наше предсказание роста – не точное, это оценка (estimate)
У нее есть стандартная ошибка (standard error) и доверительный интервал
Дальнейший анализ это не учтет!
Поэтому дальнейший анализ недооценит SE, т.е. неопределенность в результатах анализа будет на самом деле больше, чем кажется
Слайд 16Решение – multiple imputation
Применим генератор случайных чисел и сделаем для каждого пациента

несколько предсказаний
Проведем дальнейший анализ (ANOVA и проч.) отдельно для каждого набора предсказаний
Усредним результаты
Для усреднения разработаны формулы, т. наз. Rubin rule (статистик Дональд Рубин вывел эти формулы)
Слайд 17Дональд Рубин
Почетный профессор Гарвардского университета, создал основы метода multiple imputation

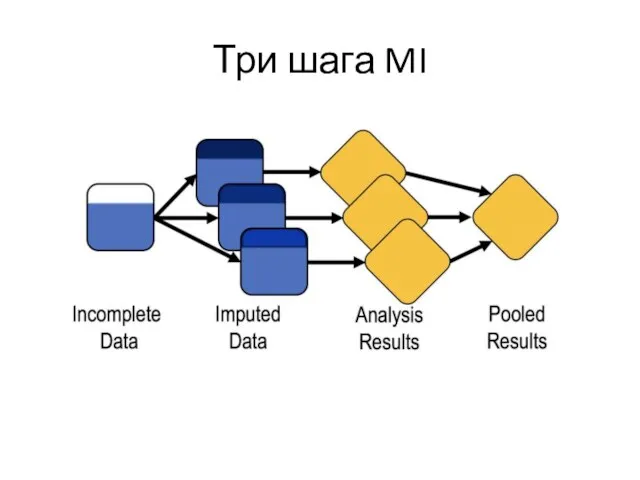
Слайд 18Три шага MI
Шаг 1 – impute несколько раз
В SAS реализуется PROC MI
Есть

несколько методов, мы их рассмотрим
Распадается на P-step и I-step
P-step (predict): построить модель
I-step (impute): выбрать случайные предсказания
В некоторых методах P-step и I-step повторяются много раз итеративно
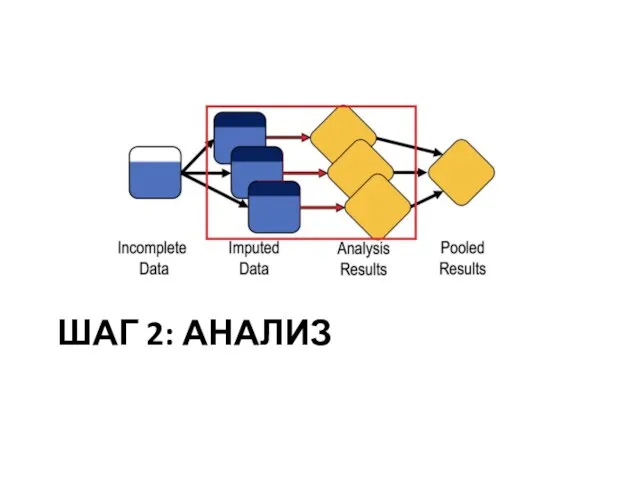
Слайд 19Три шага MI
Шаг 2: провести анализ каждого набора предсказаний
Применяем совершенно любые процедуры

SAS
BY _IMPUTATION_
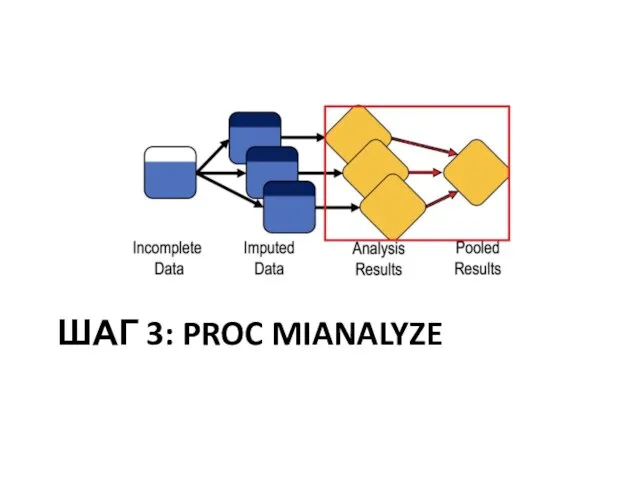
Слайд 20Три шага MI
Шаг 3:сводим вместе результаты нескольких анализов
В SAS реализуется PROC MIANALYZE
Конкретный

синтаксис зависит от процедур, примененных в шаге 2
Слайд 23PROC MI
В этом разделе мы изучим, как вызывать PROC MI. У этой

процедуры сложный синтаксис.
Небольшая оговорка. Если я составляю SAP, я обязательно вставлю в него образцы кода, как именно надо вызывать PROC MI
Но если SAP дает нам заказчик, не могу гарантировать, что в нем будут такие образцы кода
В любом случае программистам стоит понимать, что означают опции PROC MI и когда какие нужно применять
Слайд 24MI: основные вопросы
Чтобы корректно провести MI, надо ответить на такие вопросы:
Какие переменные

мы хотим “impute”?
Какие факторы включить в imputation model
Какой метод и тип модели выбрать
Сколько раз делать “multiple” imputation
Слайд 25Выбор переменных
Очевидно, мы хотим “impute” study endpoints.
Но если наш endpoint не собирается

непосредственно, а вычисляется из других переменных, то лучше impute исходные переменные!
Например, в исследованиях по псориазу применяется endpoint “PASI75”: снижение PASI на 75%, где PASI – некий балл, говорящий о тяжести болезни
Лучше impute сам PASI как непрерывную переменную и потом вычислить PASI75, а не impute PASI75 как бинарную переменную!
Слайд 26Выбор факторов
Общий совет: чем больше, тем лучше.
Факторы, которые потом включаются в модель

анализа
Факторы, которые могут быть коррелированы с переменной, которую мы пытаемся “impute”
Факторы, которые могут быть связаны с вероятностью иметь missing значение
Слайд 27Выбор факторов
Факторы, которые могут быть коррелированы с переменной, которую мы пытаемся “impute”
Другие

endpoints
Может быть малоэффективно. Если “imputed” endpoint неизвестен, то скорее всего потому, что пациент не пришел на визит, и тогда все остальные endpoints тоже неизвестны
Тот же endpoint, измеренный на других визитах/timepoints
Слайд 28Выбор факторов
Факторы, которые могут быть связаны с вероятностью иметь missing значение
Completed/Discontinued
Причина discontinuation

или “Discontinued due to AE” (yes/no)
Может быть сайт
Слайд 29Факторы и “imputed” переменные
За один раз можно “impute” несколько переменных
Более того, факторы

тоже могут иметь missing values и быть imputed
По сути PROC MI рассматривает все переменные, для “imputation” и факторы, вместе, как одну группу, и “impute” каждую на основе остальных
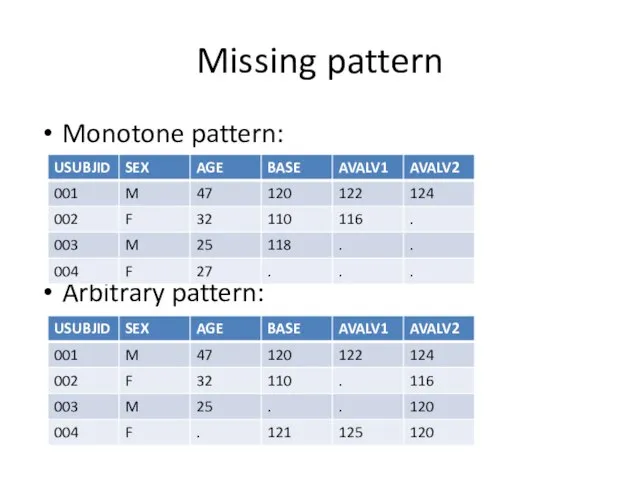
Слайд 30Missing pattern
Прежде, чем разбираться с выбором метода imputation, надо ввести понятие missing

pattern: monotone или arbitrary
Берем “imputed” переменную и все факторы, выбранные для imputation model
Monotone pattern: если какая-то из этих переменных missing, то все после нее – тоже
Иначе – arbitrary pattern
Слайд 31Missing pattern
Monotone pattern:
Arbitrary pattern:
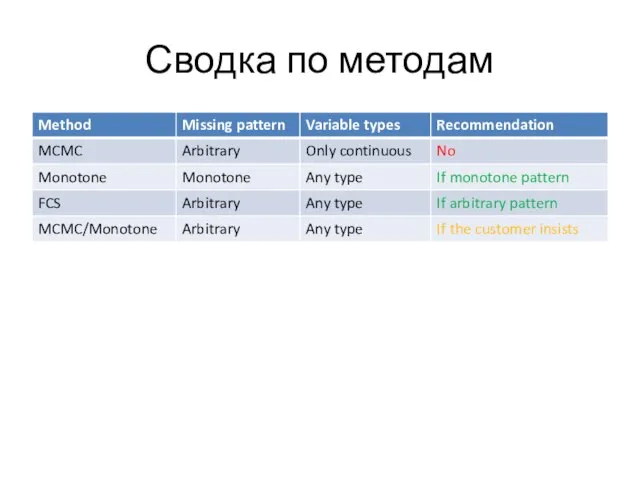
Слайд 32Методы imputation
Основные методы:
MCMC (Monte-Carlo Markov Chain)
Monotone
FCS (Fully Conditioned Specifications)
Гибридный метод MCMC/Monotone
При выборе

метода руководствуемся:
Тип переменных (imputed и факторы)
Missing pattern
Слайд 33Метод MCMC
Подразумевает, что все переменные (“imputed” и факторы) вместе имеют многомерное нормальное

распределение
Т.о. как минимум все эти переменные должны быть непрерывными
Если одна из них дискретная – метод не подходит
Missing pattern: arbitrary
Слайд 34А.А. Марков и казино Монте-Карло

Слайд 35Метод Monotone
“Imputed” переменная и факторы могут быть непрерывными, бинарными, категориальными
Missing pattern: monotone
Не

итеративный метод, работает быстрее всех
Идеален, если можем быть уверенным, что missing pattern будет monotone
Например, все факторы – baseline characteristics
Слайд 36Метод FCS
“Imputed” переменная и факторы могут быть непрерывными, бинарными, категориальными
Missing pattern: arbitrary
Самый

гибкий метод
Рекомендуется, если нет гарантии monotone pattern
Слайд 37Гибридный метод MCMC/Monotone
Устаревший метод!
Применялся до создания FCS
И тем не менее, есть заказчики-ретрограды,

которые на нем настаивают, поэтому о нем надо знать
Два шага:
сначала MCMC для imputation только промежуточных значений, чтобы «добить» до monotone pattern
Потом применяется метод Monotone
Слайд 39Типы моделей
Методы Monotone и FCS поддерживают несколько разных типов моделей
Reg: линейная регрессия
Regpmm

(regression predictive mean matching): после регрессии imputed значение выбирается среди нескольких наблюдаемых значений, близких к предсказанному регрессией
Logistic: логистическая регрессия
Discrim: дискриминантная функция
Формально для метода Monotone есть еще тип Propensity, но его не рекомендуют
Слайд 40Типы моделей
Выбор типа модели определяется типом “imputed” переменной:
Непрерывная: reg или regpmm. Рекомендация:
Переменная

с большим диапазоном и малым шагом дискретизации (например, лаб. тест, vital sign) – reg
Переменная с ограниченным диапазоном или крупным шагом дискретизации (например, балл опросника, всегда целый и в диапазоне 0-10): regpmm
Бинарная или ординальная: logistic
Номинальная: discrim
Этот тип модели лучше работает с непрерывными факторами
Не может использовать interaction terms
Слайд 41Сколько imputations делать
50 почти всегда подойдет
Если очень много данных, это может быть

долго, можно сократить до 20-25
Можно отладить программы с малым числом (5), а потом сделать перезапуск с большим числом
Достаточность к-ва imputations можно контролировать по параметру Relative Efficiency, который вычисляет PROC MI – обсудим ниже
Слайд 42Синтаксис PROC MI
proc mi ...;
var var1 var2 var3 var4 ...;
class

var1 var2 ...;
mcmc ...;
monotone ...;
fcs ...;
run;
Обычно будет только один оператор-метод из mcmc, monotone, fcs
Может быть несколько вызовов одного метода для разных переменных, но не может быть вызова нескольких разных методов
Слайд 43Опции PROC MI
data= - входной датасет
out= - выходной датасет
nimpute= - к-во imputations
Если

в датасете data N строк, то в датасете out будет N*nimpute
Будет добавлена переменная _IMPUTATION_
seed= - произвольное число, инициализирующая random number generator
Необходимо для QC, чтобы результаты не менялись при каждом перезапуске
Слайд 44Операторы var и class
В операторе var перечисляются все переменные – те, что

мы хотим “impute” и факторы для моделирования
В операторе class перечисляются те из переменных, которые являются классификационными (категориальными) – как во всех процедурах SAS.
Слайд 45Оператор MCMC
MCMC <опции>
Опции:
chain=single или chain=multiple
Нет рекомендаций, оставляем по умолчанию
Impute=monotone
Impute только до достижения

monotone pattern, применяется в гибридном методе MCMC/Monotone
Слайд 46Операторы Monotone и FCS
MONOTONE <тип модели> (imputed = factors)
FCS такой же синтаксис
MONOTONE

reg (avalv2 = sex age base avalv1)
FCS regpmm (avalv2 = sex age base avalv1)
MONOTONE logistic (avalv2 = sex age base avalv1)
FCS discrim (avalv2 = sex age base avalv1 / classeffects=include)
Опция classeffects нужна, если среди факторов есть классификационные
Слайд 47Операторы Monotone и FCS
Упрощенный вариант:
FCS REG (avalv1 avalv2);
Все переменные imputed по очереди
MONOTONE:

факторами будут все переменные из VAR, указанные раньше данной
FCS: факторами будут все переменные из VAR
Обычно указывать факторы после знака = не нужно
Нужно чтобы задать interaction factor
По какой-то причине для какой-то переменной не все факторы из var годятся
Слайд 48Дополнительные опции PROC MI
minimum=, maximum=, round=
Задается минимальное или максимальное значение для imputed

переменной и как ее округлить
После знака равенства ставится столько чисел, сколько есть переменных в операторе var
Точка означает, что данную переменную не преобразовывать
Слайд 49Дополнительные опции PROC MI
Пример:
PROC MI minimum=. . . 1 1 maximum=. .

. 100 100 round=. . . 1 1;
var sex age base avalv1 avalv2;
Переменные sex, age, base не меняются
AVALV1, AVALV2 округляются до целого и ограничиваются от 1 до 100
Опции имеют смысл для методов MCMC, MONOTONE/FCS REG. В остальных случаях imputed значение – всегда одно из наблюдаемых
Слайд 50Гибридный метод MCMC/Monotone
Два вызова PROC MI:
proc mi data=... out=mono ...;
var ...;

mcmc impute=monotone;
run;
proc mi data=mono nimpute=1 ...;
by _imputation_;
var ...;
monotone ...;
run;
Слайд 51Гибридный метод MCMC/Monotone
Что делать в первом шаге гибридного метода, если есть категориальные

факторы?
Опустить
Бинарные закодировать 0, 1
Вставить в оператор by
Слайд 52Пример PROC MI
proc mi data=... out=... nimpute=50 seed=45780;
var weight base chg4

chg8 chg12;
monotone regpmm(chg4 chg8 chg12);
run;
Слайд 53Пример PROC MI
proc mi data=… out=… nimpute=50 seed=122001;
var trtp disstab skinclass

base chg12
chg24;
class trtp disstab skinclass;
fcs regpmm(chg12=trtp disstab
skinclass base trtp*base chg24);
fcs regpmm(chg24=trtp disstab
skinclass base trtp*base chg12);
run;
Слайд 54Пример PROC MI
proc mi data=... out=... nimpute=50
seed=2031602;
var trtpn sitegr1 base

chg5-chg7;
class trtpn sitegr1;
monotone reg(chg5-chg7);
run;
Слайд 55Пример PROC MI
proc mi data=.. out=... nimpute=50 round=1
seed=45779;
by trtpn;
var

weight base chg4 chg8 chg12;
mcmc impute=monotone;
run;
Слайд 56PROC MI Output
Missing data patterns:
Простой способ узнать missing data pattern: запустить proc
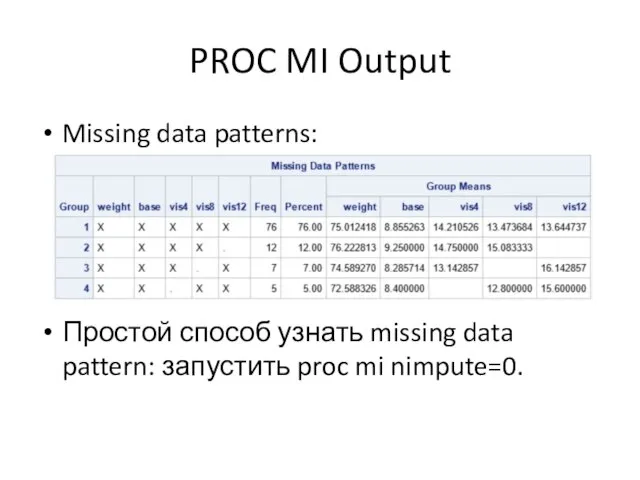
mi nimpute=0.
Слайд 57PROC MI Output
Variance information:
Обратите внимание на Relative Efficiency в последней колонке
Стремимся иметь
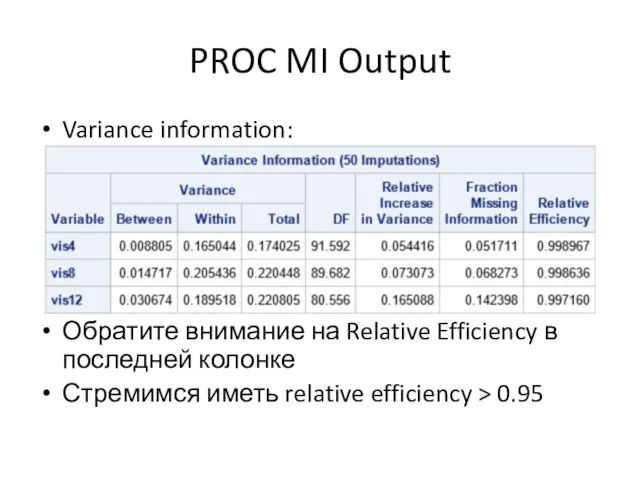
relative efficiency > 0.95
Слайд 58Relative Efficiency
“Relative” to infinite number of imputations
Что делать, если RE < 0.95?
Увеличить

nimpute
Но если при nimpute=50 имеем RE < 0.95, это говорит о том, что очень большой процент данных missing
Весь анализ под вопросом
Слайд 60Анализ multiple imputed data
Применяем любые процедуры
С оператором BY _IMPUTATION_
Сохраняем результаты в датасеты

с помощью ODS
Слайд 62PROC MIANALYZE
На входе этого шага мы имеем результаты анализа каждого из наборов

multiple imputed данных
Цель этого шага – свести их воедино и дать окончательные оценки интересующих нас параметров
Синтаксис PROC MIANALYZE будет зависеть от того, как мы проводили анализ в Шаге 2
Для ряда процедур SAS есть прямая поддержка, для остальных предусмотрен общий случай
Мы разберем наиболее часто встречающиеся варианты
Слайд 63Обработка результатов PROC MIXED
PROC MIXED реализует mixed model, но также ANOVA, ANCOVA
Обычно

обрабатываем результаты из ODS датасетов LSMeans, Diffs
Результаты PROC GLM и PROC GENMOD обрабатываются точно так же
Слайд 64Обработка результатов PROC MIXED
proc mianalyze parms=LSMeans;
class trtpn;
modeleffects trtpn;
run;
В опции parms

указываем датасет LSMeans или Diffs
В операторе modeleffects – то же, что в PROC MIXED было в LSMeans
Может быть interaction типа trtpn*avisitn
В операторе class – классификационные переменные
Для обработки Diffs может понадобиться оператор by trtpn _trtpn, если сравнений больше одного!
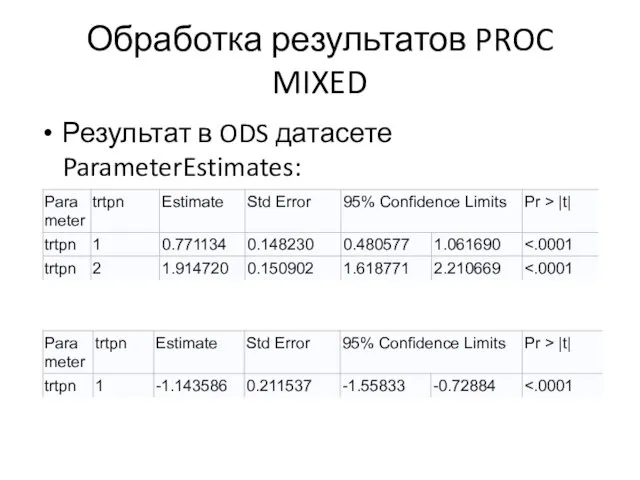
Слайд 65Обработка результатов PROC MIXED
Результат в ODS датасете ParameterEstimates:
Слайд 66Как PROC MIANALYZE понимает датасет PARMS
_Imputation_: номер imputation
Effect: имя из modeleffects
TRTPN: для
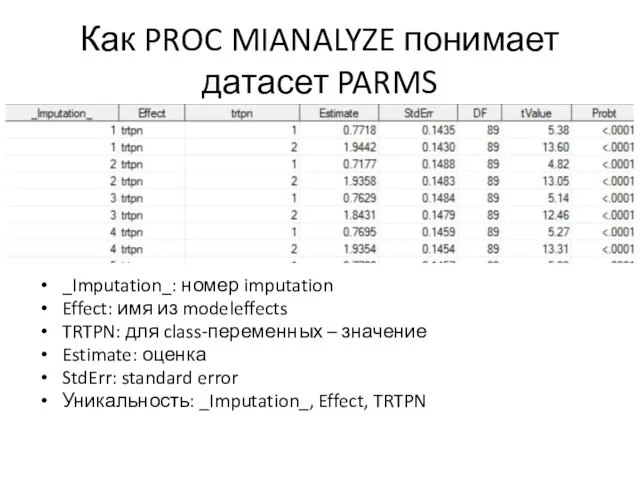
class-переменных – значение
Estimate: оценка
StdErr: standard error
Уникальность: _Imputation_, Effect, TRTPN
Слайд 67Обработка результатов PROC LOGISTIC
proc logistic data=…;
by _imputation_;
class trtpn site /

param=ref;
model avalc = trtpn site base;
run;
Сохраняем ODS датасет ParameterEstimates
proc mianalyze parms(classvar=classval)=ParameterEstimates;
class trtpn site;
modeleffects trtpn site;
run;
Отличается от обработки результатов PROC MIXED опцией classvar=classval.
Слайд 68Обработка результатов PROC LOGISTIC
В результате получаем оценки параметров модели, но как получить
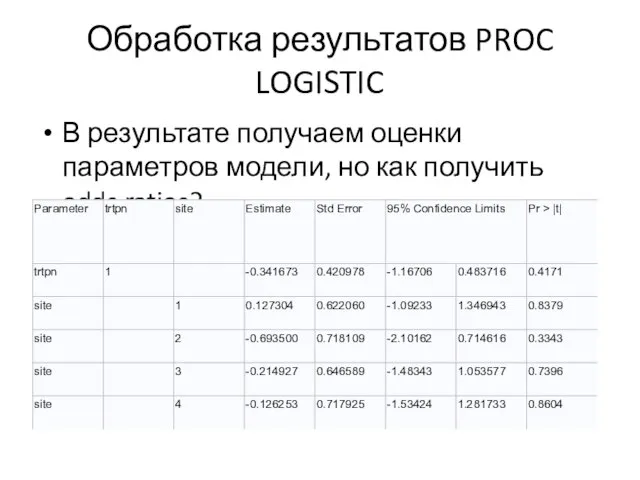
odds ratios?
Слайд 69Обработка результатов PROC LOGISTIC
Нужно экспоненциировать (функция exp) оценку параметра и доверительные пределы
Не

забываем в PROC LOGISTIC в операторе CLASS указывать опцию PARAM=REF, иначе это не сработает!
Аналогичный подход работает для Hazard Ratio в PROG PHREG
Слайд 70MIANALYZE: Общий случай
Если процедура не имеет в MIANALYZE специальной поддержки, то обрабатываем

результаты так:
Входной датасет имеет по строке на _Imputation_
В нем пары переменных: оценка и ее standard error
proc mianalyze data=...;
modeleffects est1 est2 ...;
stderr StdErr1 StdErr2 ...;
run;
Подразумевается, что переменные имеют нормальное распределение!
Опция parms для выходных датасетов процедур с особой поддержкой; опция data для общего случая
Слайд 71MIANALYZE: Wilcoxon test
Пример применения общего случая для обработки результата Wilcoxon test:
proc npar1way

data=… wilcoxon;
by _imputation_;
class trtpn;
var aval;
run;
Сохраняем ODS датасет WilcoxonTest
В нем есть переменная Z – статистика со стандартным нормальным распределением
Слайд 72MIANALYZE: Wilcoxon test
Делаем data step и добавляем в датасет WilcoxonTest переменную StdErr,

равную 1 на всех записях
proc mianalyze data=WilcoxonTest;
modeleffects Z;
stderr StdErr;
run;
Получаем p-value
Слайд 73MIANALYZE: binomial proportion
Другой пример общего случая: обработать пропорции пациентов, которые достигли какого-то

response.
Пропорция (или процент) имеет биномиальное распределение
Но если к-во пациентов велико, оно достаточно близко к нормальному, и proc mianalyze можно применить!
Слайд 74MIANALYZE: binomial proportion
proc freq data=…;
by trtpn _imputation_;
tables avalc / binomial;
run;
Сохраняем

ODS датасет Binomial
В этом датасете нас интересует пропорция и ее Asymptotic Standard Error (ASE). Датасет надо преобразовать proc transpose (или data step’ом), чтобы получить пропорцию и ASE на одной строке для каждого trtpn и _imputation_
Слайд 75MIANALYZE: binomial proportion
После этого:
proc mianalyze data=…;
by trtpn;
modeleffects _BIN_;
stderr E_BIN;
run;
Для

обработки разности пропорций рассчитываем SE разности = sqrt(SE12 + SE22)
Слайд 76MIANALYZE: прочие случаи
Обработка следующих типов анализа затруднена тем, что статистики не имеют

нормального распределения:
Chi-square test
CMH test
Fisher’s test
Kaplan-Meier estimates
Log-rank test
Correlation coefficients
Многие другие
Слайд 77MIANALYZE: прочие случаи
Общий подход:
Применить преобразование, которое переводит распределение нужной статистики к нормальному
Применить

proc mianalyze
Применить обратное преобразование
Для каждого типа анализу существуют формулы, но сегодня не будем их изучать, их очень много
В случае необходимости ищем в литературе
Слайд 79MULTIPLE IMPUTATION AND ADAM DATASETS

Слайд 80Multiple Imputation and ADaM Datasets
Должны ли мы сохранять результат PROC MI в

датасет или делать все три шага MI в рамках программы таблицы?
Рекомендация:
Если анализ с MI является основным (primary) или с MI делается более одной таблицы – сохраняем в датасет
Иначе можем все сделать в программе таблицы
Слайд 81Создание датасета с результатами MI
Рекомендация: создать один датасет без MI и другой,

отдельный, с MI
Потому что датасет с MI будет большой, наверняка понадобится иметь быстрый доступ к данным без MI (например, для листинга), а выделять изначальные данные из датасета с MI будет долго
Т.е., например, ADEF и ADEFMI
Слайд 82Создание датасета с MI
Если в imputation model участвуют данные с других визитов

или endpoints, датасет нужно транспонировать в горизонтальную структуру
Вызвать PROC MI
Напоминаю, что всегда надо задавать SEED
Транспонировать назад в вертикальную структуру
Слайд 83Создание датасета с MI (продолжение)
PROC MI никак не обозначает, какие данные были

известны, а какие были imputed
Поэтому делаем merge с изначальным датасетом по ключевым переменным, чтобы найти imputed значение и задать для них DTYPE (например ‘MI’)
Переменной _IMPUTATION_ даем допустимое имя, например IMPNO
Слайд 84Использование датасета с MI
В программе таблицы выполняем шаги 2 (анализ) и 3

(PROC MIANALYZE)
Перед вызовом PROC MIANALYZE нужно переименовать переменную IMPNO обратно в _IMPUTATION_
Слайд 85Пример программы для MI датасета
Пример кода

Слайд 87Missing Not at Random
Что, если наши данные Missing Not at Random (MNAR)?
Напомним,

это означает, что вероятность отсутствия данных зависит от самих данных
Например, пациент, на которого лекарство действует хуже, скорее выпадет из исследования, чем тот, на кого действует хорошо
Следовательно, отсутствующие данные могут быть хуже, чем наблюдаемые
Слайд 88Missing Not at Random
До сих пор мы моделировали отсутствующие данные на основе

наблюдаемых
Т.е. полагали, что отсутствующие данные примерно такие же как наблюдаемые
Но в предположении MNAR это неверно
И проверить никак нельзя. Ситуации MAR и MNAR отличаются как раз теми данными, которые неизвестны
Слайд 89Sensitivity to MAR
И что же делать?
Нужно провести sensitivity analysis, проверяющий “sensitivity” результатов

анализа к предположению MAR
Т.е. посмотреть, насколько хуже будут результаты, если отсутствующие данные хуже, чем наблюдаемые
Обычно применяется подход на основе Pattern-Mixture Models
Слайд 90Pattern-Mixture Models
Pattern-Mixture Models – широкий класс подходов, мы будем рассматривать нужный нам

частный случай
Основная идея:
Сделать предположение, у каких пациентов их missing данных могут быть хуже, чем наблюдаемые
Сделать предположение, насколько хуже они могут быть
Провести анализ с MI, при этом после шага 1 искусственно ухудшить результаты выбранных пациентов выбранным образом
Слайд 91У кого данные могут быть хуже?
У всех пациентов с missing data
У всех,

кто принимал тестовое лекарство (но не у тех, кто контрольное) (Worst case)
У тех, кто выбыл по «подозрительной» причине:
Lack of Efficacy
Adverse Event
У тех, кто выбыл после определенного визита
Комбинации условий выше и проч.
Слайд 92Насколько хуже могут быть данные?
Рассмотрим два подхода:
Control-based imputation
Penalization

Слайд 93Control-Based Imputation
Предполагаем, что состояние выбывших пациентов, принимавших тестовое лекарство аналогично состоянию

не выбывших пациентов из контрольной группы
Логично, если контрольная группа – Placebo или “Standards of Care”
Нелогично, если контроль – активное лекарство
Т.о. модель для imputation строится только по пациентам из контрольной группы
Слайд 94Penalization
Предполагаем, что missing данные хуже на какую-то величину в абсолютном или процентном

выражении
Из результата imputation вычитается некий “penalization factor”
Размер “penalization factor” должен определяться клиническими специалистами
Но возможен еще такой подход:
Вычисляем “treatment effect” из основного анализа (разность test – control)
Определяем penalization factor как какой-то процент от treatment effect
Если penalization factor = treatment effect получаем по сути control-based imputation
Слайд 95Tipping-point Analysis
Идея такая: провести анализ с penalization несколько раз, постепенно увеличивая penalization

factor, и посмотреть, при каком penalization factor меняется исход анализа, т.е., например, условие superiority перестает выполнятся (p-value становится больше 0.05)
Это значение называется tipping point
Часто берут диапазон от 0 до treatment effect с каким-то разумным шагом
Слайд 96Two-dimensional Tipping-Point
Перебирают комбинации разных penalization factors для тестового и контрольного лекарства
Смотрят, при

каких комбинация сохраняется нужных исход
Обычно применяется, когда надо показать эквивалентность (т.е. от теста и контроля ожидается одинаковый эффект)
Слайд 98MNAR Statement
Для реализации основных видов анализа MNAR в PROC MI есть оператор

MNAR
Он такой новый, что в редакторе SAS подсвечивается красным
Применим с методами MONOTONE и FCS
Если используем гибридный метод MCMC/Monotone, применяем на втором шаге
Для нестандартных подходов всегда можно доработать результат работы PROC MI специальным data step
Слайд 99Control-Based Imputation
proc mi data=… out=… nimpute=…;
var …;
class trtpn …;
fcs

reg(resp);
mnar model (resp / modelobs = (trtpn = '1'));
run;
В операторе MNAR MODEL указываем:
Imputed переменную (resp)
В опции modelobs – условие, какие записи использовать при построении модели
Слева от знака равенства - переменная
Она должна быть в CLASS, но НЕ ДОЛЖНА быть в модели
Справа – значение
В кавычках, даже если числовое
Можно указать несколько через пробел (trtpn = ‘1’ ‘2’)
Слайд 100Control-Based Imputation
Что если стоит такая задача:
Применить control-based imputation для пациентов из тестовой

группы, которые выбыли из-за “lack of efficacy”
Применить обычный метод (MAR) к остальным
Можно сделать так:
Два вызова PROC MI
Один с оператором MNAR без treatment в модели
Второй без оператора MNAR с treatment в модели
Соединяем (merge) результаты, берем результат первого оператора для пациентов из тестовой группы, которые выбыли из-за “lack of efficacy”, второго для остальных
Слайд 101Penalization
proc mi data=… out=… nimpute=… seed=…;
var trtpn resp …;
class trtpn

…;
fcs reg(resp);
mnar adjust (resp / adjustobs=(trtpn='2') shift=-0.2);
run;
В операторе MNAR ADJUST указываем
Imputed переменную (resp)
ADJUSTOBS: как каким записям применяем penalization (синтаксис условия такой же, как в modelobs)
SHIFT: сколько добавить к результату
Также можно указать SCALE: на сколько умножить результат
SIGMA: к результату добавляется нормально распределенная случайная величина со средним SHIFT и с.к.о. SIGMA
Слайд 102Tipping-point analysis
Tipping-point analysis можно реализовать так:
Делаем макрос, в нем в цикле вызываем

PROC MI с оператором MNAR ADJUST с разными значениями SHIFT (значение задается макро-переменной)
%do i = 0 %to 10;
%let shift = %sysevalf(1 + &i/10);
proc mi data=... out=imputed&i nimpute=... seed=...;
...
mnar adjust (resp / adjustobs=(trtpn='2') shift=-&shift);
run;
%end;
Можно применять разный SEED для разных shifts
Результаты соединяем, например, PROC APPEND
В PROC MIANALYZE задаем “by shift”
Слайд 1032-dimensional tipping-point analysis
Для реализации 2-dimensional tipping-point analysis можно задавать две опции ADJUST

с разными условиями:
%do i = 1 %to 10;
%let shift1 = %sysevalf(1 + &i/10);
%do j = 1 %to 10;
%let shift2 = %sysevalf(1 + &j/10);
proc mi data=... out=imputed&i._&j nimpute=... seed=...;
...;
mnar adjust (resp / adjustobs=(trtpn='1') shift=-&shift1)
adjust (resp / adjustobs=(trtpn='2') shift=-&shift2);
run;
%end;
%end;
В PROC MIANALYZE задаем “by shift1 shift2”
Слайд 104Tipping-point – вопросы времени выполнения
PROC MI может работать относительно долго
При tipping-point анализе,

особенно 2-dimensional, PROC MI вызывается много раз, и время выполнения может оказаться очень большим
Вариант: провести отладку с малым числом NIMPUTE, затем один раз запустит с большим
Слайд 105Tipping-point – вопросы времени выполнения
Можно рассмотреть вариант с «ручным» penalization
Вы вызываете PROC

MI один раз без оператора MNAR
Затем «размножаете» каждую строку в цикле data step, «ухудшая» результат нужных записей на нужную величину – это может оказаться быстрее
Результат не будет идентичен оператору MNAR из-за разной работы генератора случайных чисел, но в среднем аналогичен
Поэтому если применять этот метод, то одновременно в основной программе и QC
Слайд 106Penalization c бинарными переменными
Метод penalization наиболее понятен для непрерывных переменных, но также

применим к бинарным
“Penalization” заключается в том, что уменьшается вероятность положительного исхода
Оператор MNAR поддерживает такой вариант, но есть проблемы
Слайд 107Penalization c бинарными переменными
Для imputation бинарных переменных PROC MI использует логистическую регрессию
Вспомним,

как она работает. В этой модели моделируется log odds вероятности нужного исхода: log(p/(1-p))
Log(p/(1-p)) = линейная комбинация факторов
Слайд 108Penalization c бинарными переменными
Т.о. MI работает так:
P-step:
Подобрать коэффициенты модели для моделирования log

odds на тех записях, в которых исход известен
I-step:
Для записей, где исход missing, по полученной формуле рассчитать log odds
По нему рассчитать вероятность удачного исхода: p = (1+exp(LogOdds))/exp(LogOdds)
Назначить удачный исход с вероятностью p, неудачный – 1-p
Слайд 109Penalization c бинарными переменными
Оператор MNAR может вставить penalization между шагами 2 и

3, т.е. ухудшить log odds
Для этого ему нужно указать, какое из значений переменной - «удачный» исход, который мы хотим ухудшить:
mnar adjust (avalc(event='Y') / adjustobs=… shift=…)
Слайд 110Penalization c бинарными переменными
Проблема: log odds сложно интерпретировать:
Уменьшение log odds на X

означает уменьшение “odds” успеха в exp(X) раз. Это не очень интуитивно
Т.е. если мы хотим уменьшить вероятность положительного исхода в тестовой группе на 0.1 (или в 2 раза), на сколько надо изменить log odds? Невозможно сказать, зависит от вероятности для данного пациента
Слайд 111Penalization c бинарными переменными
Возможен альтернативный подход к penalization без оператора MNAR
При этом

подходе penalization происходит между шагами 3 и 4, т.е. ухудшаем вероятность удачного исхода – это гораздо легче понять и интерпретировать
Это пример ситуации, когда оператор MNAR не поможет – придется дорабатывать результат PROC MI вручную
Слайд 112Penalization c бинарными переменными
Схема этого процесса:
Запускаем PROC MI без оператора MNAR. Используем

опцию details, которая сохраняет параметры модели в датасет
Используя этот датасет вручную рассчитываем log odds
Вручную рассчитываем вероятность удачного успеха и уменьшаем ее как хотим у кого хотим
Назначаем удачный исход с вероятностью p, неудачный – 1-p. Можно применить функцию rantbl.










































































































 goCoworking. Система бронирования коворкингов
goCoworking. Система бронирования коворкингов Медиастрана
Медиастрана Как зарегистрироваться на сайте предварительного голосования Единой России
Как зарегистрироваться на сайте предварительного голосования Единой России Список типовых блоков сайта
Список типовых блоков сайта Як створювати схеми класифікації об’єктів?
Як створювати схеми класифікації об’єктів? Инструкция подачи запроса на получение сертификата с использованием онлайн сервиса
Инструкция подачи запроса на получение сертификата с использованием онлайн сервиса TWITCH. О продукте
TWITCH. О продукте Создание альтернативного сайта КЖРЭУП Железнодорожное
Создание альтернативного сайта КЖРЭУП Железнодорожное Работа со звуком
Работа со звуком Hours Calterm
Hours Calterm Проникновение и деятельность вируса Spora на ПК
Проникновение и деятельность вируса Spora на ПК Информационный сегмент
Информационный сегмент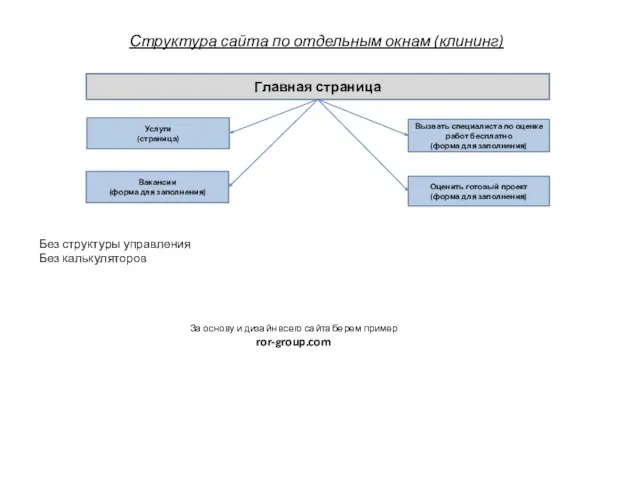 Структура сайта по отдельным окнам (клининг)
Структура сайта по отдельным окнам (клининг) Источники угроз, которые несет всемирная сеть
Источники угроз, которые несет всемирная сеть Мастерская
Мастерская Информатика. Моё хобби
Информатика. Моё хобби циклы Обмена отчеты ФНС
циклы Обмена отчеты ФНС Программирование (C++). Символьные строки
Программирование (C++). Символьные строки Информационно-аналитический инструментарий в системе информационного обеспечения функционирования фирмы
Информационно-аналитический инструментарий в системе информационного обеспечения функционирования фирмы Компьютерный вирус. Происхождение термина
Компьютерный вирус. Происхождение термина Услуги компьютерных сетей. Удаленная база данных
Услуги компьютерных сетей. Удаленная база данных Компьютерные телекоммуникации: назначение, структура, ресурсы
Компьютерные телекоммуникации: назначение, структура, ресурсы Основные конструкции языка Java. Лекция 6
Основные конструкции языка Java. Лекция 6 БАРС Web - Электронная школа
БАРС Web - Электронная школа Информационные технологии в профессиональной деятельности
Информационные технологии в профессиональной деятельности Apache Maven
Apache Maven Соответствие между блок- схемой и алгоритмической структурой
Соответствие между блок- схемой и алгоритмической структурой Понятие операционной системы
Понятие операционной системы