Компьютерная арифметика

var a: real;
i: integer;
begin
a:=0; i:=1;
repeat
a+=0.1; i+=1;
until a=1; writeln (i)
end.

Компьютерная арифметика
§ 26. Особенности представления чисел в компьютере
§ 27. Хранение в памяти целых чисел
§ 28. Операции с целыми числами
§ 29. Хранение в памяти вещественных чисел
§ 30. Операции с вещественными числами

Компьютерная арифметика
§ 26. Особенности представления чисел в компьютере

Предельные значения чисел
В математике нет предельных значений!
В компьютере – конечное число деталей, ограниченное количество разрядов.
10000?

Предельные значения чисел
система счисления с основанием B
K разрядов
Переполнение разрядной сетки — это ситуация, когда число, которое требуется сохранить, не умещается в имеющемся количестве разрядов вычислительного устройства.

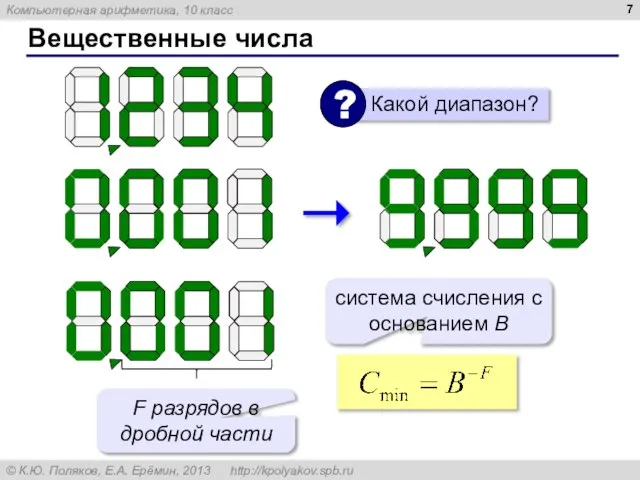
Вещественные числа
система счисления с основанием B
F разрядов в дробной части

Неточность представления
0,1234567
1,3211
1,3212
1,3214

Сравнение вещественных чисел
хранится неточно!
неточный результат!
допустимая погрешность (10-6)

Дискретность
Целые числа дискретны.
Вещественные числа непрерывны.
Компьютер работает только с дискретными данными.
При дискретизации может происходить потеря информации (искажение данных).
Большинство трудностей связано с кодированием вещественных чисел.

Компьютерная арифметика
§ 27. Хранение в памяти целых чисел

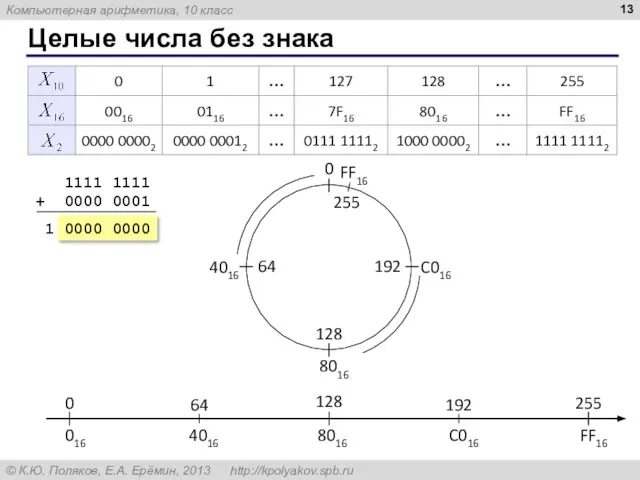
Целые числа без знака (unsigned)
78 = 10011102
Беззнаковые данные – не могут быть отрицательными.
биты
младший
старший
старший полубайт
старшая цифра
младший полубайт
младшая цифра
416
E16
10011102 = 4E16 = ‘N’

Целые числа без знака
1111 1111
+ 0000 0001
1 0000 0000

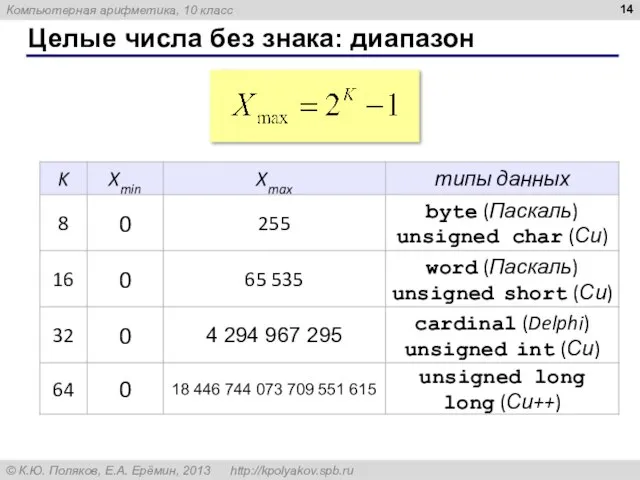
Целые числа без знака: диапазон

Целые числа со знаком
Старший (знаковый) бит числа определяет его знак. Если он равен 0, число положительное, если 1, то отрицательное.
Прямой код:
78 = 10011102
– 78 = –10011102
≥ 0
< 0
операции с положительными и отрицательными числами выполняются по-разному!

Целые числа со знаком
Идея: «– 1» должно быть представлено так, чтобы при сложении с числом «1» получить 0.
1111 1111
+ 0000 0001
1 0000 0000
-1 → 255
1
256
Для 8-битных чисел: код числа «–X» равен двоичному коду числа 256 – X (дополнение до 256).

Как построить дополнительный код?
Алгоритм А0: перевести число 2K – X в двоичную систему счисления.
для вычислений требуется K+1 разряд
Алгоритм А1:
перевести число X в двоичную систему счисления;
построить обратный код, выполнив инверсию всех битов (заменить 0 на 1 и наоборот);
к результату добавить 1.
78 = 010011102
10110001
-78 → 10110010
← инверсия
+1

Как построить дополнительный код?
Алгоритм А2:
перевести число X-1 в двоичную систему счисления;
выполнить инверсию всех битов.
78 - 1 = 77 = 010011012
← инверсия
Алгоритм А3:
перевести число X в двоичную систему счисления;
выполнить инверсию всех старших битов числа, кроме младшей единицы и нулей после нее.
78 = 010011102
-78 → 10110010
-78 → 10110010
← инверсия

Целые числа со знаком

Целые числа co знаком: диапазон

Компьютерная арифметика
§ 28. Операции с целыми числами

Сложение и вычитание
0000 0101
1111 0111
+
1111 1100
-4 ←

Переполнение
знаковый бит
дополнительный бит
00100001
01100000
+
010000001
96
33
-127
S’
S
0
0
1
0
11011111
10100000
+
101111111
-96
-33
127
S’
S
1
1
0
1

Умножение
9
5
→45
00001001
×
00000101
00001001
00000000
00001001
0000101101
+
-9
5
→-45
11110111
×
00000101
11110111
00000000
11110111
10011010011
+

Поразрядные логические операции
Поразрядные операции выполняются с отдельными битами числа и не влияют на остальные.
регистр
Операция «НЕ» (инверсия, not):
R
not R

Логическая операция «И» (and, &)
данные
маска
Маска – константа, которая определяет область применения логической операции к битам многоразрядного числа.
D
D and M
M
AA16
6С16
2816
AA16 and 6C16 = ?

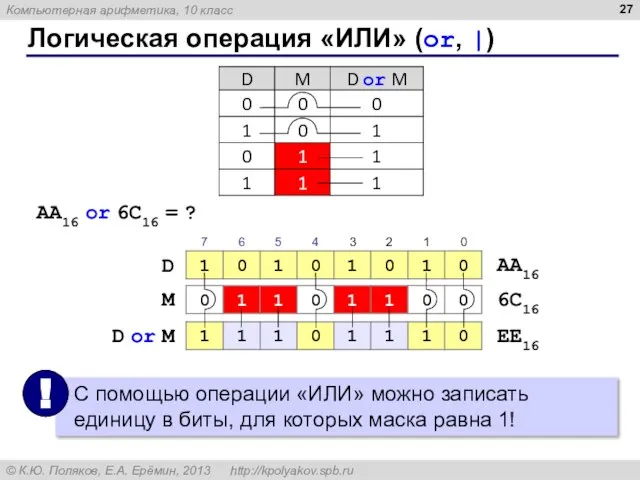
Логическая операция «ИЛИ» (or, |)
D
D or M
M
AA16
6С16
EE16
AA16 or 6C16 = ?

Операция «исключающее ИЛИ» (xor, ^)
D
D xor M
M
AA16
6С16
C616
AA16 xor 6C16 = ?

Битовые логические операции (итог)
R
1) отключить лампочки 2 и 1, не трогая остальные
R = R and F916
2) включить лампочки 7 и 4
R = R or 9016
3) изменить состояние лампочек 5, 4 и 2
R = R xor 3416

Шифрование с помощью xor
Идея: (A xor B) xor B =
A
Текст: 2*2=4
Коды символов:
'2' = 3216 = 001100102
'*' = 2A16 = 001010102
'=' = 3D16 = 001111012
'4' = 3416 = 001101002

Шифрование с помощью xor
Исходный текст: 2*2=4
'2' → 3216 xor 1716 =
'*' → 2A16 xor 1716 =
'=' → 3D16 xor 1716 =
'4' → 3416 xor 1716 =
2516 → '%'
3D16 → '='
2A16 → '*'
2316 → '#'
Маска: 23 = 1716 = 000101112
Зашифрованный текст: %=%*#
Расшифровка:
'%' → 2516 xor 1716 =
'=' → 3D16 xor 1716 =
'*' → 2A16 xor 1716 =
'#' → 2316 xor 1716 =
3216 → '2'
2A16 → '*'
3D16 → '='
3416 → '4'

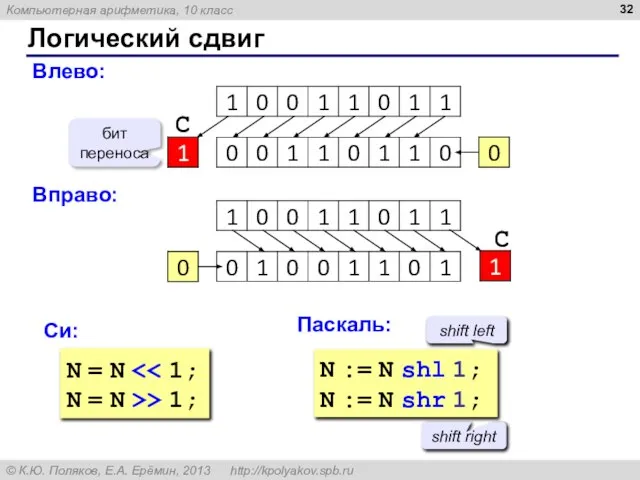
Логический сдвиг
Влево:
бит переноса
С
Вправо:
С
Си:
Паскаль:
N = N << 1;
N = N >> 1;
N := N shl 1;
N := N shr 1;
shift left
shift right

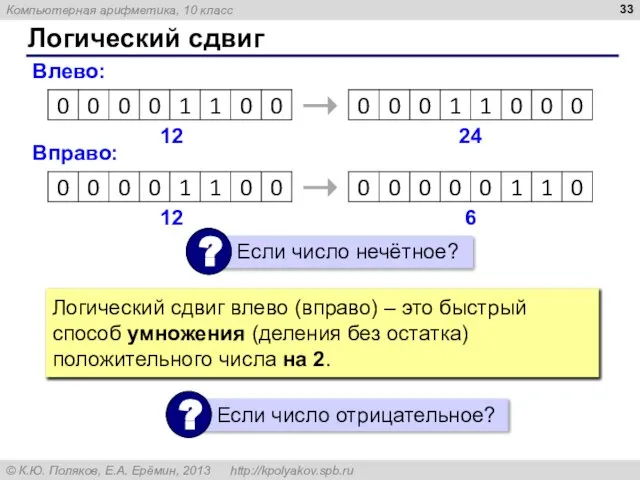
Логический сдвиг
Влево:
12
24
Вправо:
12
6
Логический сдвиг влево (вправо) – это быстрый способ умножения (деления без остатка) положительного числа на 2.

Арифметический сдвиг (вправо)
–12
С
– 6
Примеры:
20
15
11
3
1
→ 10
→ 7
→ 5
→ 1
→ 0
–20
–15
–11
–3
–1
→ –10
→ –8
→ –6
→ –2
→ –1
Арифметический сдвиг вправо – деление на 2 нацело с округлением «вниз» (к ближайшему меньшему целому).

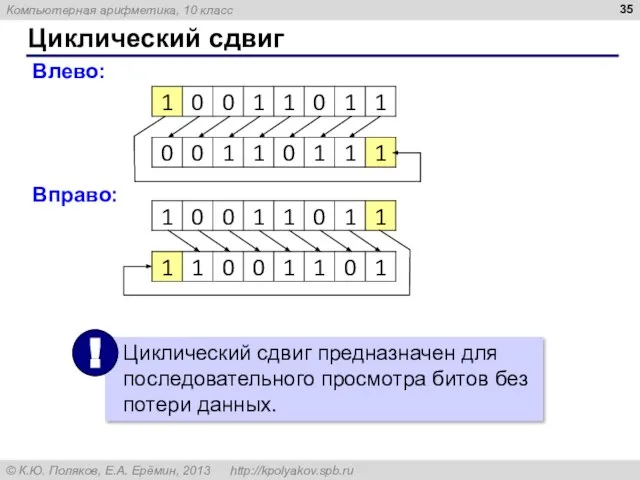
Циклический сдвиг
Влево:
Вправо:

Пример
Задача: в целой переменной N (32 бита) закодирована
информация о цвете пикселя в RGB:
Записать в переменные R, G, B составляющие цвета.
Вариант 1:
Обнулить все биты, кроме G.
Маска для выделения G: 0000FF0016
Сдвинуть вправо так, чтобы число G передвинулось в младший байт.
Си:
G =(N & 0xFF00) >> 8;
Паскаль:
G:=(N and $FF00) shr 8;

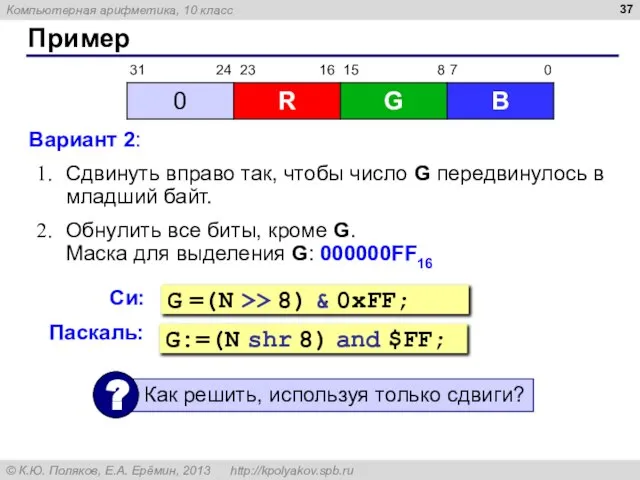
Пример
Вариант 2:
Сдвинуть вправо так, чтобы число G передвинулось в младший байт.
Обнулить все биты, кроме G.
Маска для выделения G: 000000FF16
Си:
G =(N >> 8) & 0xFF;
Паскаль:
G:=(N shr 8) and $FF;

Пример
Си:
R =
B =
Паскаль:
R:=
B:=

Компьютерная арифметика
§ 29. Хранение в памяти вещественных чисел

Хранение вещественных чисел
С фиксированной запятой (в первых ЭВМ):
для больших и маленьких чисел нужно масштабирование
0,000000000000012345
123450000000000000,0
С плавающей запятой (автоматическое масштабирование):
положение
запятой
цифры числа
1,2345·10-14
1,2345·1017

Хранение вещественных чисел
Теоретически оптимальный вариант (целая часть = 0):
0,0012345 = 0,12345·10-2
12,345 = 0,12345·102
всегда 0
один разряд расходуется впустую!
Экономный вариант (целая часть от 1 до B):
основание системы счисления
0,0012345 = 1,2345·10-3
12,345 = 1,2345·101
повышение точности при конечном числе разрядов

Нормализация
Нормализованная форма: значащая часть Z удовлетворяет условию 1 ≤ Z < B, где B – основание системы счисления (стандарт IEEE 754).
Пример:
17,25 = 10001,012 = 1,0001012·24
5,375 =
7,625 =
27,875 =
13,5 =
0,125 =
всегда 1, её можно не хранить в памяти!

Число обычной точности (single)
-17,25 = -10001,012 = -1,0001012·24
single: 4 байта = 32 бита
мантисса = дробная часть Z
порядок со
смещением
знак
p = 4 + 127 = 131 = 100000112
С
1
8
A
0
0
0
0
для single

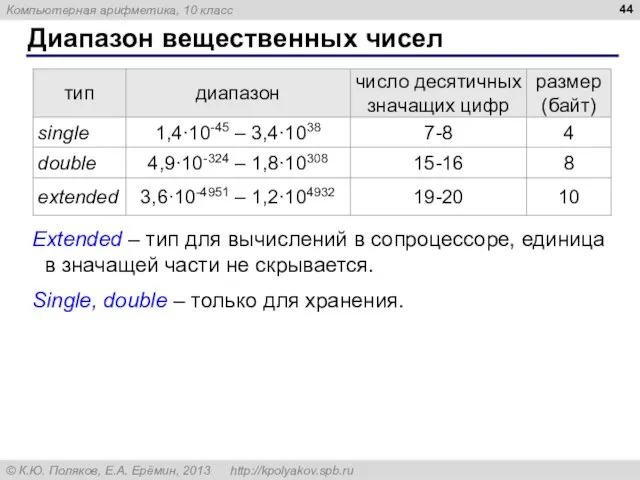
Диапазон вещественных чисел
Extended – тип для вычислений в сопроцессоре, единица в значащей части не скрывается.
Single, double – только для хранения.

Компьютерная арифметика
§ 30. Операции с вещественными числами

Сложение и вычитание
порядки выравниваются до большего
значащие части складываются (или вычитаются)
результат нормализуется
1,2345·10 – 5 + 1,2345·105 = ?
Пример:
7,25 = 111,012 = 1,11012·22
1,75 = 1,112 = 1,112·20
1,75 = 0,01112·22
10,012·22 = 1,0012·23

Умножение и деление
1,2345·10 – 5 · 1,2345·105 = ?
значащие части умножаются (или делятся)
порядки складываются (или вычитаются)
результат нормализуется
Пример:
1,75 = 1,112 = 1,112·20
6 = 1102 = 1,12·22
1,112·1,12 = 10,1012
10,1012·22 = 1,01012·23
0 + 2 = 2

Конец фильма
ПОЛЯКОВ Константин Юрьевич
д.т.н., учитель информатики
ГБОУ СОШ № 163, г. Санкт-Петербург
[email protected]
ЕРЕМИН Евгений Александрович
к.ф.-м.н., доцент кафедры мультимедийной дидактики и ИТО ПГГПУ, г. Пермь
[email protected]