Содержание
- 2. Ключевые слова множество пустое множество пересечение двух множеств объединение двух множеств дополнение множества мощность множества формула
- 3. Понятие множества Множество — совокупность объектов произвольной природы, которая рассматривается как единое целое. !
- 4. Способы задания множества Какие множества можно задавать перечислением всех элементов? ?
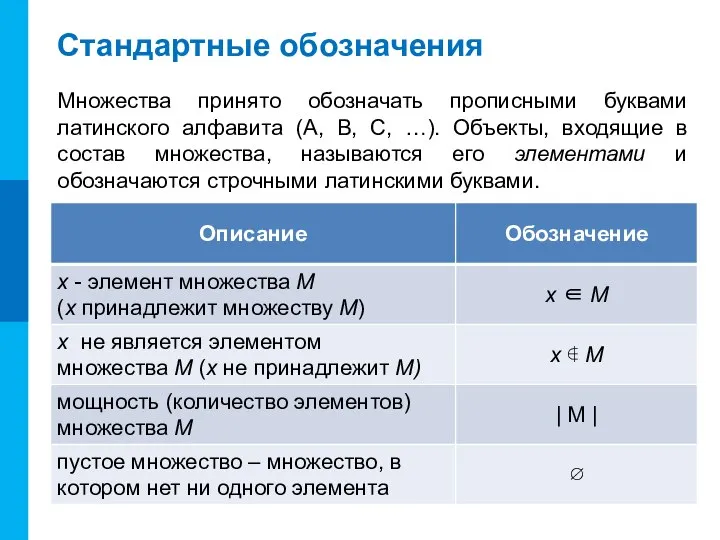
- 5. Стандартные обозначения Множества принято обозначать прописными буквами латинского алфавита (A, B, C, …). Объекты, входящие в
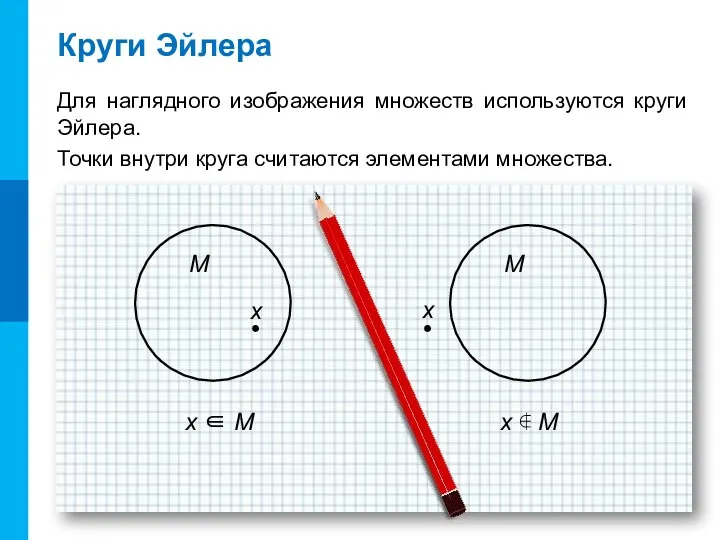
- 6. Круги Эйлера Для наглядного изображения множеств используются круги Эйлера. Точки внутри круга считаются элементами множества. x
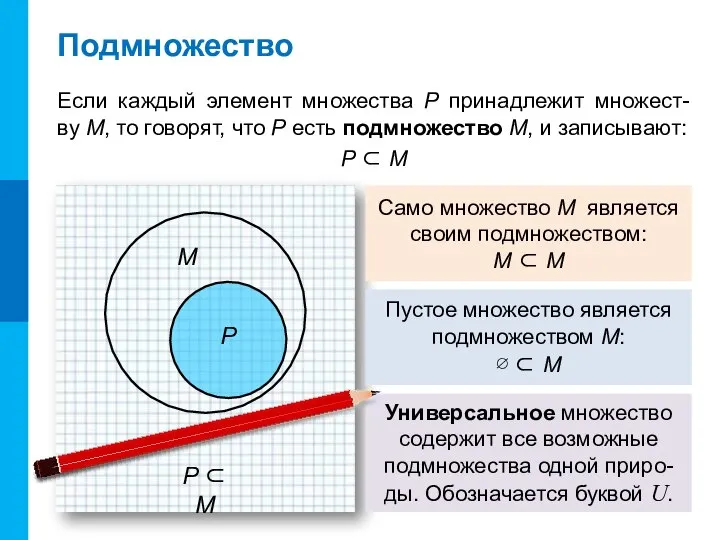
- 7. Подмножество Если каждый элемент множества P принадлежит множест- ву М, то говорят, что P есть подмножество
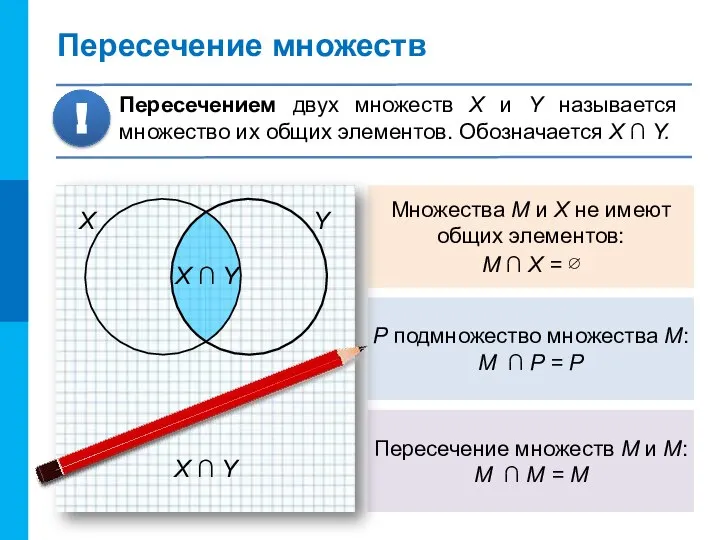
- 8. Множества M и X не имеют общих элементов: M ∩ X = ∅ P подмножество множества
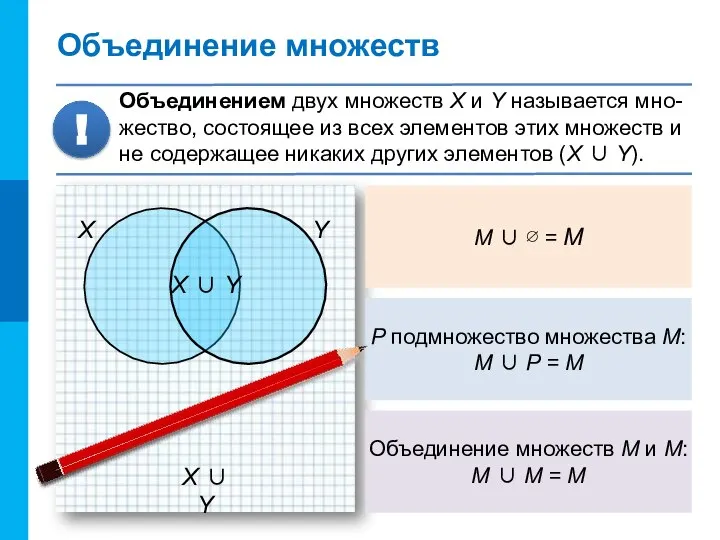
- 9. X ∪ Y Объединение множеств Объединением двух множеств X и Y называется мно-жество, состоящее из всех
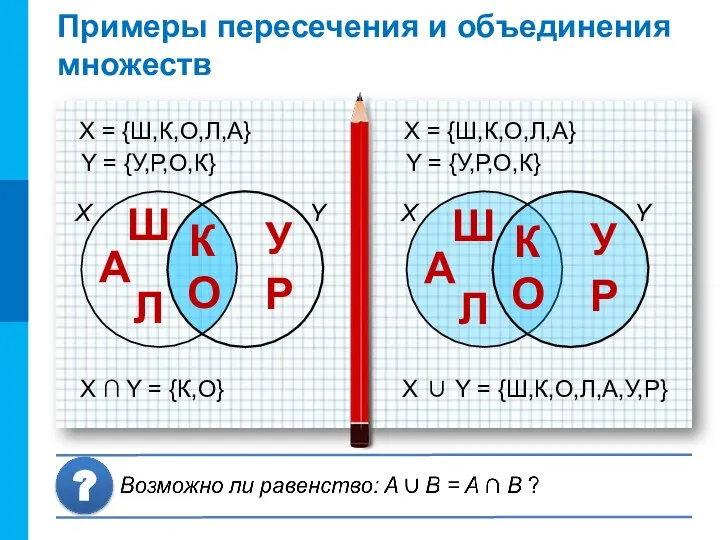
- 10. Примеры пересечения и объединения множеств X Y X ∪ Y = {Ш,К,О,Л,А,У,Р} X = {Ш,К,О,Л,А} Y
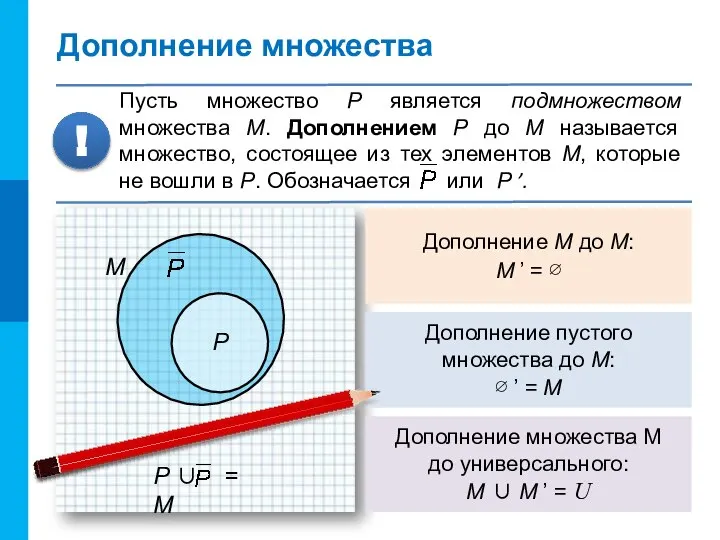
- 11. Дополнение множества Пусть множество P является подмножеством множества М. Дополнением P до М называется множество, состоящее
- 12. Мощность множества Мощностью конечного множества называется число его элементов. Мощность множества X обозначается |X|. ! Мощность
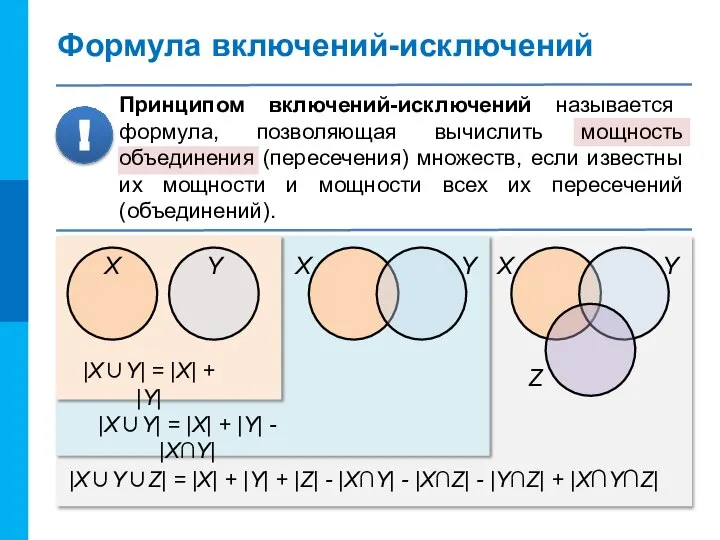
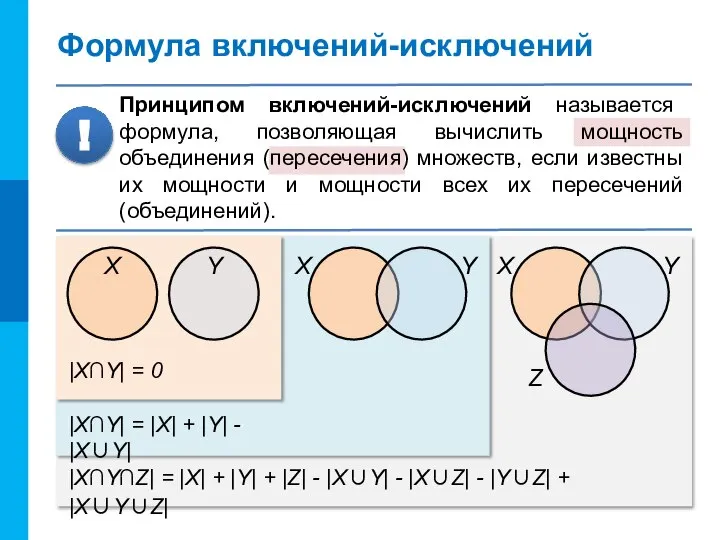
- 13. Формула включений-исключений Принципом включений-исключений называется формула, позволяющая вычислить мощность объединения (пересечения) множеств, если известны их мощности
- 14. Формула включений-исключений Принципом включений-исключений называется формула, позволяющая вычислить мощность объединения (пересечения) множеств, если известны их мощности
- 15. - 10 Вопросы и задания В зимний лагерь отправляется 100 старшеклассников. Почти все они увлекаются сноубордом,
- 16. Самое главное Множество — это совокупность объектов произвольной природы, которая рассматривается как единое целое. Пересечением двух
- 17. Вопросы и задания 1. Сколько натуральных чисел от 1 до 1000 включительно делятся на 3 или
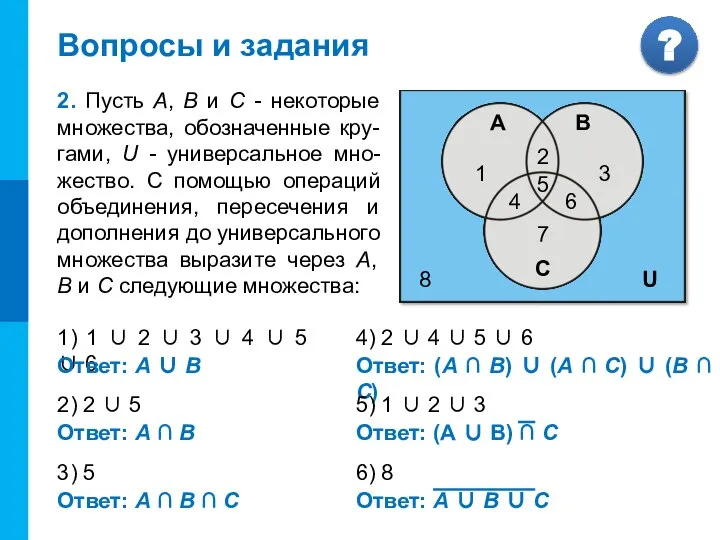
- 18. 1) 1 ∪ 2 ∪ 3 ∪ 4 ∪ 5 ∪ 6 Ответ: А ∪ В
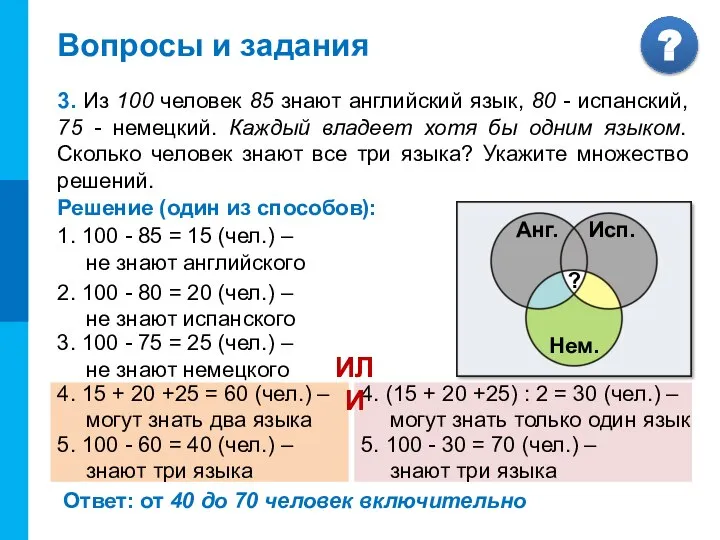
- 19. Вопросы и задания 3. Из 100 человек 85 знают английский язык, 80 - испанский, 75 -
- 21. Скачать презентацию







 Сетевые технологии и решения
Сетевые технологии и решения Информационная безопасность
Информационная безопасность Установка КриптоАРМ
Установка КриптоАРМ Презентация на тему Ввод информации в память компьютера
Презентация на тему Ввод информации в память компьютера  Организация вычислений в электронных таблицах
Организация вычислений в электронных таблицах Поиск информации в систематическом каталоге
Поиск информации в систематическом каталоге Программирование циклических алгоритмов
Программирование циклических алгоритмов Программные продукты серии Microinvest Склад Pro – преимущества и возможности
Программные продукты серии Microinvest Склад Pro – преимущества и возможности Объектно-ориентированное программирование
Объектно-ориентированное программирование Погашение через терминалы КАССА 24
Погашение через терминалы КАССА 24 Brief for a website IBox company
Brief for a website IBox company Молодежная медиасфера
Молодежная медиасфера Выпускная квалификационная работа: Разработка цикла лабораторных работ на платформе 1C: Предприятие 8.3
Выпускная квалификационная работа: Разработка цикла лабораторных работ на платформе 1C: Предприятие 8.3 Платформа Freescale Semiconductor для реализации беспроводных решений ZigBee / 802.15.4 / SMAC
Платформа Freescale Semiconductor для реализации беспроводных решений ZigBee / 802.15.4 / SMAC Образовательная платформа Ё-стади
Образовательная платформа Ё-стади Информационные технологии. Информатизация общества
Информационные технологии. Информатизация общества ДП
ДП Обратная польская нотация (RPN)
Обратная польская нотация (RPN) Социальная сеть как основа современной социальной структуры
Социальная сеть как основа современной социальной структуры OMG! Essence: единая теория программной инженерии?
OMG! Essence: единая теория программной инженерии? Презентация на тему Алгоритм и компьютерная программа
Презентация на тему Алгоритм и компьютерная программа  Современная структура глобальной сети интернет
Современная структура глобальной сети интернет Императивное программирование
Императивное программирование Создание текстового документа с использованием программы Microsoft Power Point
Создание текстового документа с использованием программы Microsoft Power Point Время думать. Информатика
Время думать. Информатика Реле управления, цифровые технологии и логические схемы
Реле управления, цифровые технологии и логические схемы ЕГЭ-2022. Задачи № 4. Коды и кодирование
ЕГЭ-2022. Задачи № 4. Коды и кодирование Платформа мониторинга и анализа социальных медиа Крибрум
Платформа мониторинга и анализа социальных медиа Крибрум