Нейронные сети

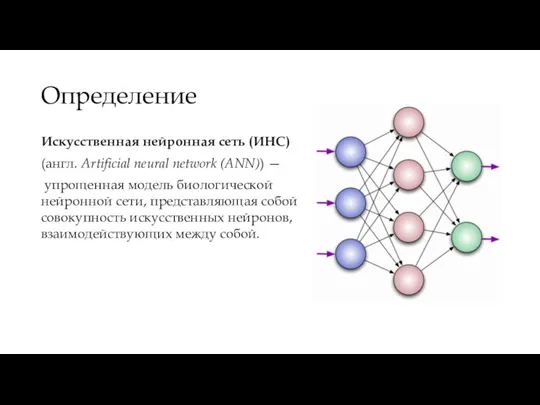
Определение
Искусственная нейронная сеть (ИНС)
(англ. Artificial neural network (ANN)) —
упрощенная модель биологической нейронной сети, представляющая собой совокупность искусственных нейронов, взаимодействующих между собой.

Задачи, решаемые нейронными сетями
Классификация/распознавание образов.
Кластеризация/категоризация
Аппроксимация функций.
Предсказание/прогноз
Оптимизация
Ассоциативная память.
Управление.

В общем случае все вышеуказанные задачи, решаемые нейронными сетями, можно свести к двум основным:
Задача классификации
заключается в формировании нейронной сетью в процессе обучения гиперповерхности в пространстве признаков, разделяющей признаки на классы. И выходы обученной нейронной сети соответствуют распознанному классу входного вектора (набора признаков).
Задача регрессии
заключается в аппроксимации нейронной сетью произвольной нелинейной функции. В этом случае значение функции снимается с выхода нейронной сети, а входами являются аргументы.

Биологический нейрон и формальная модель нейрона Маккалоки и Питтса
Биологический нейрон имеет вид, представленный на слайде. В 1943 году Дж. Маккалоки и У. Питт предложили формальную модель биологического нейрона как устройства, имеющего несколько входов (входные синапсы – дендриты), и один выход (выходной синапс – аксон).

Дендриты получают информацию от источников информации (рецепторов) Xi, в качестве которых могут выступать и нейроны. Набор входных сигналов {Xi} характеризует объект, его состояние или ситуацию, обрабатываемую нейроном.
Текущее состояние нейрона определяется, как взвешенная сумма его входов:
а выход нейрона есть функция его состояния: y = f (s).

Активационная функция нейрона
Нелинейная функция f называется активационной и может иметь различный вид:

Сигмоидная функция
Одной из наиболее распространенных является нелинейная функция с насыщением, так называемая логистическая функция или сигмоид (т.е. функция S-образного вида):
Следует отметить, что сигмоидная функция дифференцируема на всей оси абсцисс, что используется в некоторых алгоритмах обучения.

Простейшая нейронная сеть

Машинное обучение нейронной сети на примерах
Обучение классической нейронной сети состоит в подстройке весовых коэффициентов каждого нейрона.
Обучающая выборка
Вектор {xα} характеризует систему признаков конкретного объекта α обучающей выборки, зафиксированную S-элементами.
Вектор {yα} характеризует картину возбуждения нейронов при предъявлении нейронной сети конкретного объекта α обучающей выборки.

Будем называть нейронную сеть обученной на данной обучающей выборке, если при подаче на вход сети вектора {xα} на выходе всегда получается соответствующий вектор {yα} т.е. каждому набору признаков соответствуют определенные классы.

Итерационный алгоритм обучения НС
Шаг 0: Начальные значения весов всех нейронов полагаются случайными.
Шаг 1: Сети предъявляется входной образ xα, в результате формируется выходной образ.
Шаг 2: Вычисляется вектор ошибки, делаемой сетью на выходе.

Итерационный алгоритм обучения НС
Шаг 3: Вектора весовых коэффициентов корректируются таким образом, что величина корректировки пропорциональна ошибке на выходе и равна нулю если ошибка равна нулю:
– модифицируются только компоненты матрицы весов, отвечающие ненулевым значениям входов;
– знак приращения веса соответствует знаку ошибки, т.е. положительная ошибка (значение выхода меньше требуемого) проводит к усилению связи;
– обучение каждого нейрона происходит независимо от обучения остальных нейронов, что соответствует важному с биологической точки зрения, принципу локальности обучения.

Итерационный алгоритм обучения НС
Шаг 4: Шаги 1-3 повторяются для всех обучающих векторов.
Один цикл последовательного предъявления всей выборки называется эпохой. Обучение завершается по истечении нескольких эпох, если выполняется по крайней мере одно из условий:
– когда итерации сойдутся, т.е. вектор весов перестает изменяться;
– когда полная просуммированная по всем векторам абсолютная ошибка станет меньше некоторого малого значения.
Данный метод обучения был назван Ф.Розенблаттом «методом коррекции с обратной передачей сигнала ошибки». Имеется в виду передача сигнала ошибка от выхода сети на ее вход, где и определяются, и используются весовые коэффициенты. Позднее этот алгоритм назвали «α- правилом».