Обмен ключами по схеме Диффи-Хеллмана

Лекция 9. Обмен ключами по схеме Диффи-Хэллмана
План лекции:
2. Алгоритм обмена ключами
1. Введение
3. Возможности использования алгоритм Диффи-Хэллмана

Лекция 9. Обмен ключами по схеме Диффи-Хэллмана
1. Введение
Алгори́тм Ди́ффи — Хе́ллмана (англ. Diffie-Hellman, DH) — алгоритм, позволяющий двум сторонам получить общий секретный ключ, используя незащищенный от прослушивания канал связи. Алгоритм был впервые опубликован Уитфилдом Диффи (Whitfield Diffie) и Мартином Хеллманом в 1976 году.

Лекция 9. Обмен ключами по схеме Диффи-Хэллмана
В 2002 году Хеллман предложил называть данный алгоритм «Диффи — Хеллмана — Меркля», признавая вклад Меркля в изобретение криптографии с открытым ключом.
Цель схемы — обеспечить двум пользователям защищенную возможность сообщить друг другу ключ, чтобы они могли прибегнуть к ней для шифрования последующих сообщений. Сам по себе алгоритм ограничивается процедурой обмена ключами.

Лекция 9. Обмен ключами по схеме Диффи-Хэллмана
2. Алгоритм обмена ключами
Эффективность алгоритма Диффи-Хеллмана опирается на трудность вычисления дискретных логарифмов.
Формально дискретный логарифм можно определить следующим образом. Сначала определяется первообразный корень простого числа р как число, степени которого порождают все целые числа от 1 до р - 1.

Лекция 9. Обмен ключами по схеме Диффи-Хэллмана
Это значит, что если а является первообразным корнем простого числа р, то все числа
a mod р , a2 mod р , ..., ap-l mod р
должны быть разными и представлять все целые числа от 1 до р - 1 в некоторой перестановке.
Для любого целого числа b и любого первообразного корня а простого числа р однозначно определяется показатель степени i, при котором
b = ai mod р , где 0 < i < (р - 1).

Лекция 9. Обмен ключами по схеме Диффи-Хэллмана
Этот показатель степени обычно называется дискретным логарифмом, или индексом b по основанию а, рассматриваемому по модулю р. Это значение записывается в форме inda,p(b).
сотовый телефон Sagem vectroTEL X8 обеспечивает абсолютную конфиденциальность переговоров посредством специальной встроенной системы шифрования, базирующейся на использовании алгоритма Диффи-Хеллмана с 1024-битным ключом

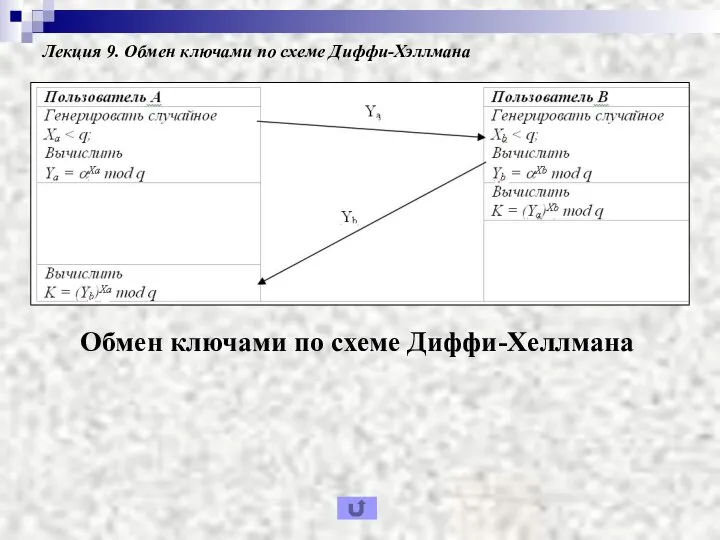
Лекция 9. Обмен ключами по схеме Диффи-Хэллмана
Алгоритм обмена ключами по схеме
Диффи-Хеллмана

Лекция 9. Обмен ключами по схеме Диффи-Хэллмана
В этой схеме имеется два открытых для всех числа: простое число q и целое число α, являющееся первообразным корнем q. Предположим, пользователи А и В намерены обменяться ключами.
Пользователь А выбирает случайное целое число Хa < q и вычисляет
Ya = αХа mod q .

Лекция 9. Обмен ключами по схеме Диффи-Хэллмана
Точно так же пользователь В независимо выбирает случайное целое число Хв < q и вычисляет
Yb = αХb mod q.
Каждая сторона сохраняет значение X в тайне и делает значение Y свободно доступным другой стороне.

Лекция 9. Обмен ключами по схеме Диффи-Хэллмана
Пользователь А вычисляет ключ по формуле
К = (Yb)Хa mod q,
а пользователь В — по формуле
К = (Ya)Хb mod q.
Эти две формулы вычисления дают одинаковые результаты.
К = (Yb)Xa mod q = (αXb mod q)Xa mod q =
= (αXb )Xa mod q = αXaXb mod q = (αXa)Xb mod q=
= (αXa mod q)Xb mod q = (Ya)Xb mod q.

Лекция 9. Обмен ключами по схеме Диффи-Хэллмана
Итак, обе стороны обменялись секретным ключом. А поскольку при этом ХА и ХB были только в личном использовании и поэтому сохранились в тайне, противнику придется работать только с q, α, Ya и Yb. Таким образом, ему придется вычислять дискретный логарифм, чтобы определить ключ.
Например, чтобы определить ключ пользователя В, противнику нужно вычислить
Xb = indα,q (Yb).
После этого он сможет вычислить ключ К точно так же, как это делает пользователь В.

Лекция 9. Обмен ключами по схеме Диффи-Хэллмана
Защищенность обмена ключами по схеме Диффи-Хеллмана опирается фактически на то, что в то время, как степени по модулю некоторого простого числа вычисляются относительно легко, вычислять дискретные логарифмы оказывается очень трудно.
Для больших простых чисел последнее считается задачей практически неразрешимой.

Лекция 9. Обмен ключами по схеме Диффи-Хэллмана
Пример. Обмен ключами строится на использовании простого числа q = 97 и его первообразном корне α = 5. Пользователи А и В выбирают секретные ключи Хa =36 и Хb = 58 соответственно.
Каждый вычисляет свой открытый ключ:
Ya = 536 = 50 mod 97 ,
Yb = 558 = 44 mod 97 .

Лекция 9. Обмен ключами по схеме Диффи-Хэллмана
После того как пользователи обменяются открытыми ключами, каждый из них может вычислить общий секретный ключ:
К = (Yb)Xa mod 97 = 4436 = 75 mod 97,
К = (Ya)Xb mod 97 = 5058 = 75 mod 97 .
Имея {50, 44}, противнику не удастся с легкостью вычислить 75.

Лекция 9. Обмен ключами по схеме Диффи-Хэллмана
Обмен ключами по схеме Диффи-Хеллмана

Лекция 9. Обмен ключами по схеме Диффи-Хэллмана
3. Возможности использования алгоритм Диффи-Хэллмана
Для примера другой возможности использования алгоритма Диффи-Хеллмана рассмотрим некоторую группу пользователей (например, всех пользователей локальной сети) и предположим, что каждый из этих пользователей должен сгенерировать секретное значение Хa для долгосрочного применения и вычислить открытое значение Ya.

Лекция 9. Обмен ключами по схеме Диффи-Хэллмана
Все полученные таким образом открытые значения вместе с глобальными открытыми значениями q и α сохраняются централизованно в некотором каталоге. В любой момент пользователь В может получить доступ к открытому значению пользователя А, вычислить секретный ключ и использовать его для пересылки шифрованного сообщения пользователю А.

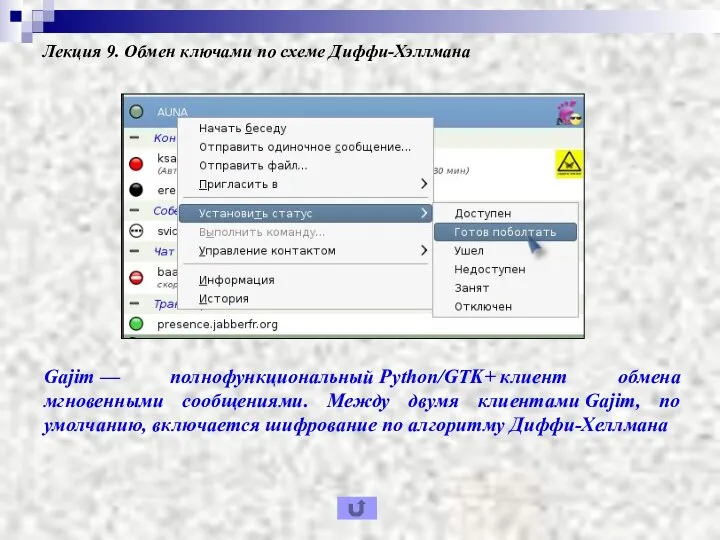
Лекция 9. Обмен ключами по схеме Диффи-Хэллмана
Gajim — полнофункциональный Python/GTK+ клиент обмена мгновенными сообщениями. Между двумя клиентами Gajim, по умолчанию, включается шифрование по алгоритму Диффи-Хеллмана

Лекция 9. Обмен ключами по схеме Диффи-Хэллмана
Если централизованно хранящийся каталог надежен, то этот форма коммуникации обеспечивает как конфиденциальность, так и определенную степень аутентификации. Поскольку только пользователи А и В могут определить ключ, другой пользователь не может прочитать сообщение (конфиденциальность). Получатель А знает, что только пользователь В мог создать сообщение, используя этот ключ (аутентификация). Однако такая схема не защищена от атак на основе воспроизведения сообщений.

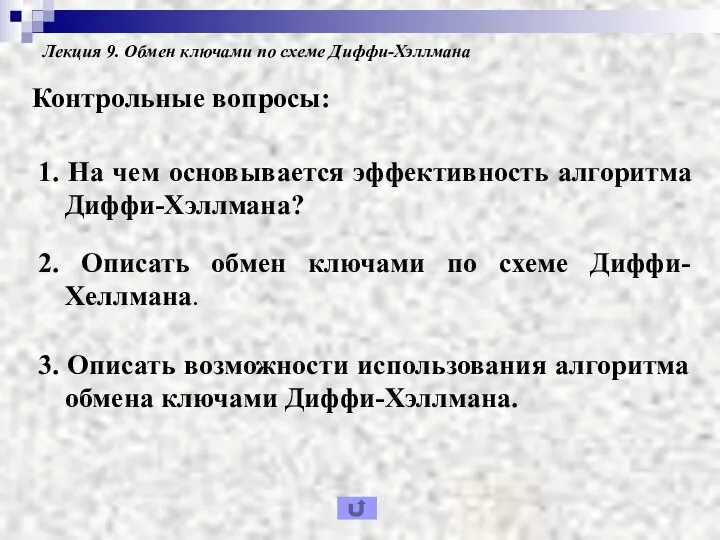
Лекция 9. Обмен ключами по схеме Диффи-Хэллмана
Контрольные вопросы:
1. На чем основывается эффективность алгоритма Диффи-Хэллмана?
2. Описать обмен ключами по схеме Диффи-Хеллмана.
3. Описать возможности использования алгоритма обмена ключами Диффи-Хэллмана.

Список используемых источников:
Бубнов А.А. Основы информационной безопасности. – М.: Академия, 2017. - 256 с.
Ерохин В.В. Безопасность информационных систем. - М. : Флинта, 2016. - 184 с.
Гашков С.Б. Криптографические методы защиты информации. - М.: Академия, 2010. - 300с.
Мельников В.П. Информационная безопасность. – М.: Академия, 2013. - 336 с.