Обобщенная модель нейрона. Персептрон (структура, алгоритмы обучения). Решение задачи распознавания образов с помощью НС
Содержание
- 2. в противном случае. 1943 – формальный нейрон (МакКаллок, Питтс): если ; в противном случае. 1958 –
- 3. ПРОБЛЕМА ИСКЛЮЧАЮЩЕГО ИЛИ (Exclusive OR, XOR) → [М. Мински, С. Пейперт, 1969] Таблица истинности функции XOR
- 4. Решение проблемы – 2-хслойная НС: Таблица истинности: = ! Условия возбуждения нейронов:
- 5. ОБОБЩЕННАЯ МОДЕЛЬ НЕЙРОНА
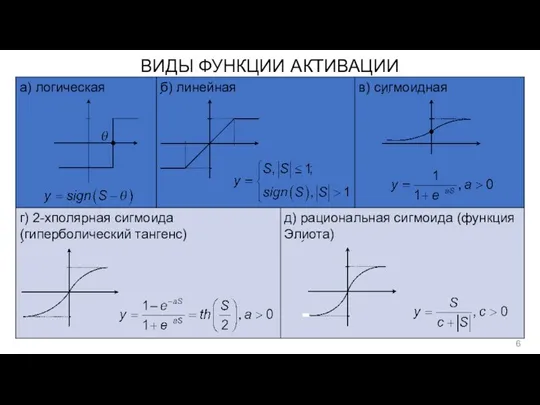
- 6. ВИДЫ ФУНКЦИИ АКТИВАЦИИ
- 7. ПЕРСЕПТРОН (структура) 1958 – однослойный персептрон (Ф. Розенблат) → (от англ. Perception – «восприятие») 1958 –
- 8. ПЕРСЕПТРОН (процедура обучения) – вектор эталонов, (желаемых выходов) НС; – вектор ошибки обучения НС; Цель обучения:
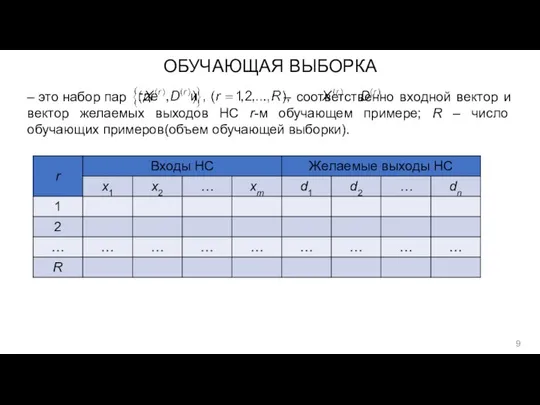
- 9. ОБУЧАЮЩАЯ ВЫБОРКА – это набор пар – соответственно входной вектор и вектор желаемых выходов НС r-м
- 10. АЛГОРИТМЫ ОБУЧЕНИЯ ПЕРСЕПТРОНА СКО: где n – число выходов НС; R – объем обучающей выборки. Градиентный
- 11. СЛОЖНОСТИ ПРОЦЕССА ОБУЧЕНИЯ «зависание» в локальных минимумах метод «тяжелого» шарика: где регуляризация процесса обучения: где –
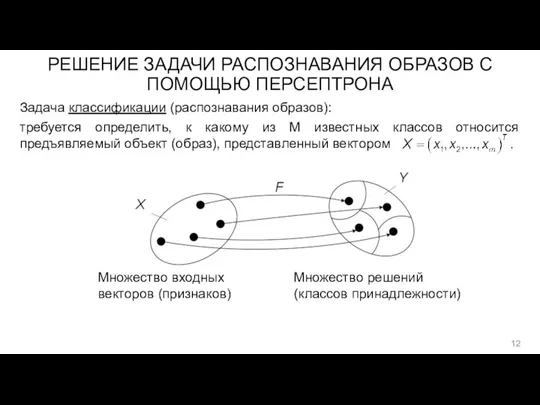
- 12. РЕШЕНИЕ ЗАДАЧИ РАСПОЗНАВАНИЯ ОБРАЗОВ С ПОМОЩЬЮ ПЕРСЕПТРОНА Задача классификации (распознавания образов): требуется определить, к какому из
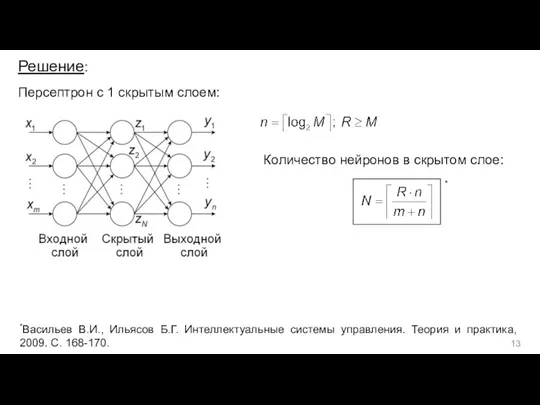
- 13. Решение: Персептрон с 1 скрытым слоем: Количество нейронов в скрытом слое: * *Васильев В.И., Ильясов Б.Г.
- 15. Скачать презентацию

![ПРОБЛЕМА ИСКЛЮЧАЮЩЕГО ИЛИ (Exclusive OR, XOR) → [М. Мински, С. Пейперт, 1969] Таблица истинности функции XOR](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/979454/slide-2.jpg)






 Моделирование. Информационный процесс
Моделирование. Информационный процесс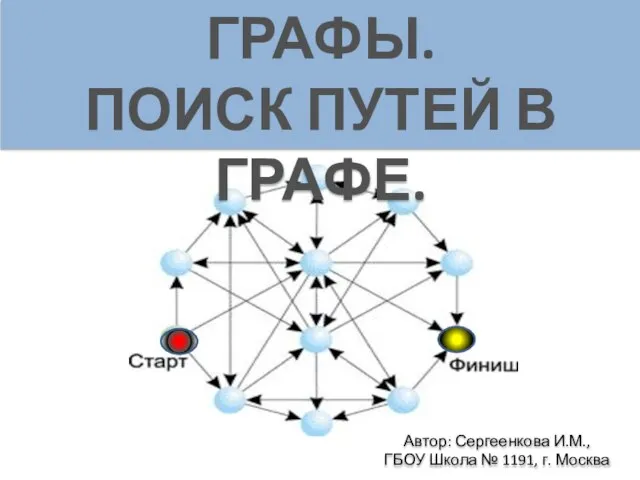 Презентация на тему Графы. Поиск путей в графе
Презентация на тему Графы. Поиск путей в графе  БИТ. Управление доступом (СКУД)
БИТ. Управление доступом (СКУД) Собрание для пожертвования
Собрание для пожертвования Программирование на языке Си#. Форма
Программирование на языке Си#. Форма Защита информации техническими методами в информационно-телекоммуникационных системах на предприятии
Защита информации техническими методами в информационно-телекоммуникационных системах на предприятии Лекция 1. Общая характеристика процессов сбора, передачи, обработки и накопления информации
Лекция 1. Общая характеристика процессов сбора, передачи, обработки и накопления информации Дизайн. О приложении
Дизайн. О приложении Примеры логистики процедуры ОСКЭ - 2016 (2 этап аккредитационного экзамена)
Примеры логистики процедуры ОСКЭ - 2016 (2 этап аккредитационного экзамена) Требования к оформлению презентаций
Требования к оформлению презентаций Зайчик. Анимация
Зайчик. Анимация نگاه کلی به سیستم عامل
نگاه کلی به سیستم عامل Растровая и векторная графика
Растровая и векторная графика The Internet
The Internet Дизайнер интерфейсов
Дизайнер интерфейсов Нейронные сети и их разновидности
Нейронные сети и их разновидности Презентация "NetSchool" - скачать презентации по Информатике
Презентация "NetSchool" - скачать презентации по Информатике Математические основы информатики. Единицы представления информации. (Тема 3)
Математические основы информатики. Единицы представления информации. (Тема 3) Методы и средства передачи информации. Лекция 4. Часть 1
Методы и средства передачи информации. Лекция 4. Часть 1 Информационная война и кибервойна: сущность и соотношение понятий
Информационная война и кибервойна: сущность и соотношение понятий Весна идет!
Весна идет! Процедуры и функции. Лабораторная работа
Процедуры и функции. Лабораторная работа Ветвление программы, циклы
Ветвление программы, циклы Електронні таблиці MS Excel
Електронні таблиці MS Excel Best practices tools: Development in the team
Best practices tools: Development in the team Редактирование текста
Редактирование текста История развития математической логики
История развития математической логики Hashtag agency 2021
Hashtag agency 2021