Содержание
- 2. Оглавление 1. Знакомство #1: простейшие задачи 2. Работа с делимостью #2: “прямые” остатки 3. Обработка остатков
- 3. Что представляет из себя 27-я задача? Задача №27, закрепленная за последним номером, традиционно считается самой сложной.
- 4. Какие виды 27-х задач существуют? поиск количества пар/групп элементов по определенным критериям поиск суммы/произведения элементов по
- 5. Поиск количества пар/групп (некие условия) Работаем с “прямыми” и “обратными” остатками, речь пойдёт о кратности элементов
- 6. Поиск суммы/произведения (некие условия) Работаем с поиском максимальных и минимальных элементов, совместной их обработкой, увеличивающимися постепенно
- 7. Поиск длины подпоследовательности (некие условия) Демоверсия | Работаем с массивами, списками, множествами, словарями
- 8. Распределением по группам (некие условия) Работаем с массивами, списками, прямыми и обратными остатками
- 9. Экзотические (дичайшие) задачи И остатки, и массивы, и множества, и словари, и списки, и строки, и
- 10. Как ещё можно классифицировать 27-е задачи? обработка одной последовательности (один ряд чисел) обработка двойной последовательности (ряды
- 11. Зачем нужен ЯП? Зачем же нужен ЯП при решении 27-х задач? Приведем банальный пример. “Дана последовательность
- 12. Каков необходимый минимум знаний и навыков? Базовый уровень владения ЯП >=: здесь без вариантов Теория чисел:
- 13. С чего следует начинать при подготовке? Начать можно с 17-х задач нового формата, которые предполагают k
- 14. Предупреждение и наставление! В разделах ПРАКТИКА по блокам я НЕ БУДУ давать подробное разъяснение, а задачи
- 15. Где брать файлы для практики? В разделах ПРАКТИКА по блокам, если Ваше решение будет отличаться от
- 16. Знакомство #1: простейшие задачи Решим легчайшие задачи, что будут являться некой подводкой к дальнейшему изучению реальных
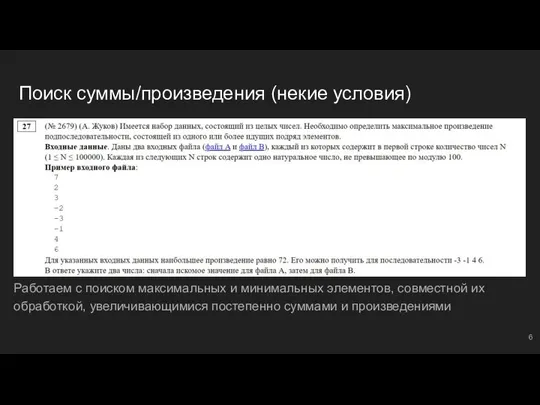
- 17. #1: №1 В файле ‘27.txt’ представлена последовательность N целых чисел. В первой строке находится число N,
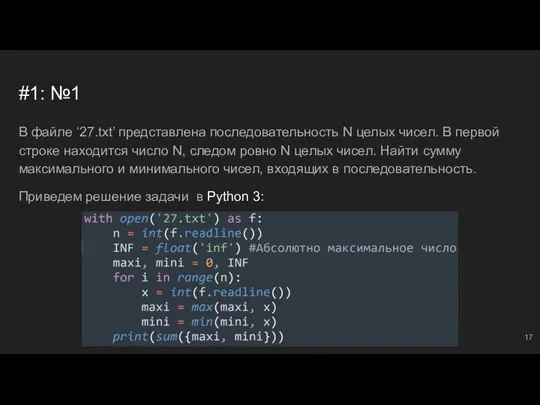
- 18. #1: №2 В файле ‘27.txt’ представлена последовательность N целых чисел. В первой строке находится число N,
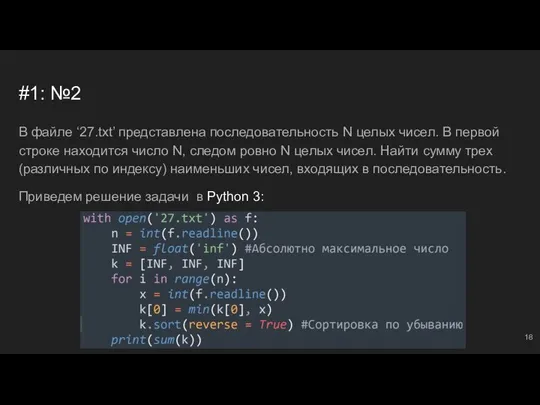
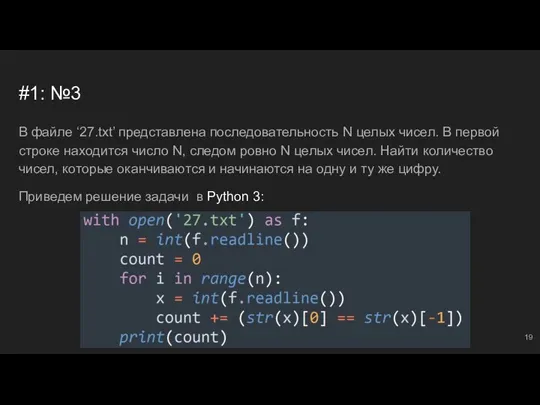
- 19. #1: №3 В файле ‘27.txt’ представлена последовательность N целых чисел. В первой строке находится число N,
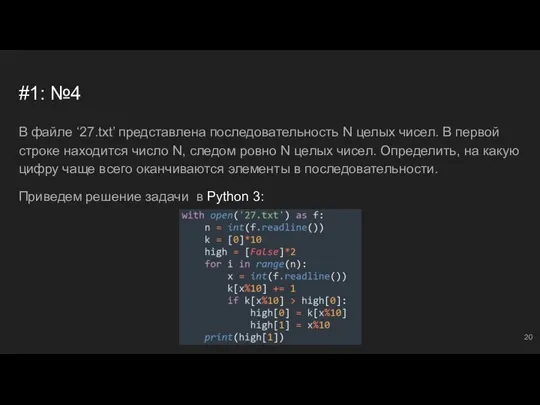
- 20. #1: №4 В файле ‘27.txt’ представлена последовательность N целых чисел. В первой строке находится число N,
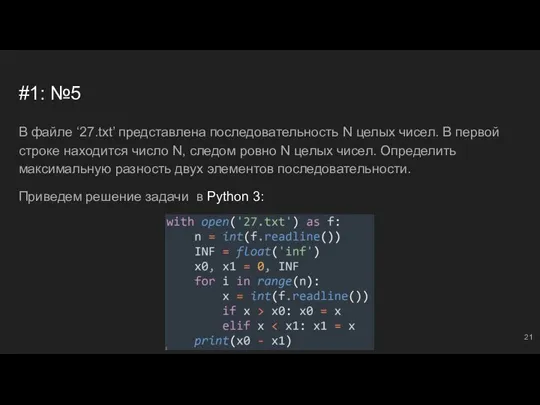
- 21. #1: №5 В файле ‘27.txt’ представлена последовательность N целых чисел. В первой строке находится число N,
- 22. Работа с делимостью #2: “прямые” остатки В этом блоке разберёмся с “прямыми“ остатками, в будущем рассмотрим
- 23. “Прямой” остаток ((x + y) / z) = (x / z + y / z) !
- 24. “Прямой” остаток ((z + z) / z) = (z / z + z / z) =
- 25. “Прямой” остаток ((x * y) / z) = (x / z * y / z) !
- 26. “Прямой” остаток ((z * z) / z) = 0 ! Каков остаток мы имеем при делении
- 27. “Прямой” остаток ((x * z) / z) = 0 ! Каков остаток мы имеем при делении
- 28. Закрепим материал, ответив на вопросы... Какой остаток от деления на 3 получается в результате произведения чисел
- 29. Ответы и решения (796 * 295432) % 3 ⇔ (796 % 3 = 1) * (295432
- 30. Работа с делимостью #2: простейшие задачи Решим легчайшие задачи, связанные с делимостью и остатками. Закрепим изученный
- 31. #2: №1 В файле ‘27.txt’ представлена последовательность N целых чисел. В первой строке находится число N,
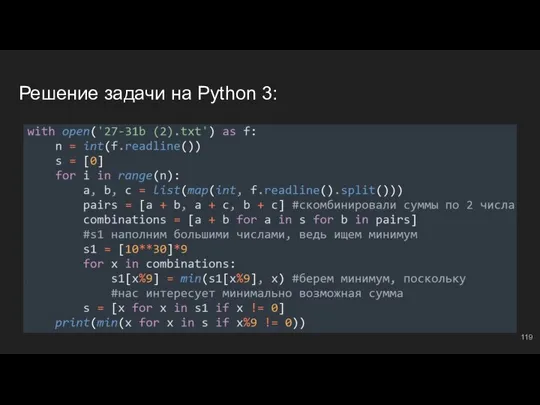
- 32. Решение задачи на Python 3:
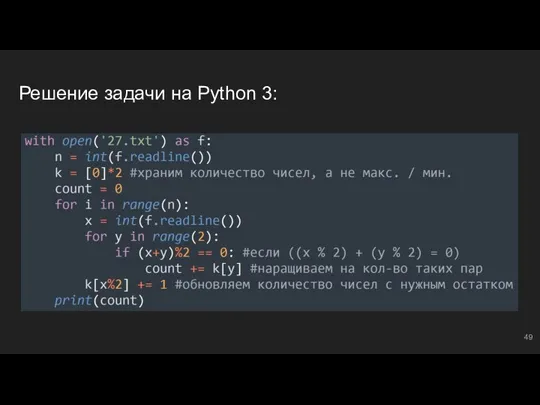
- 33. #2: №2 В файле ‘27.txt’ представлена последовательность N целых чисел. В первой строке находится число N,
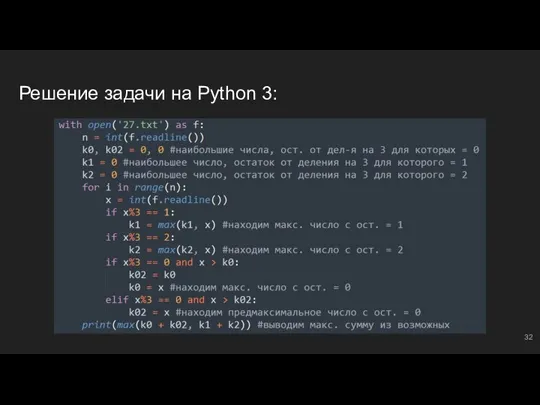
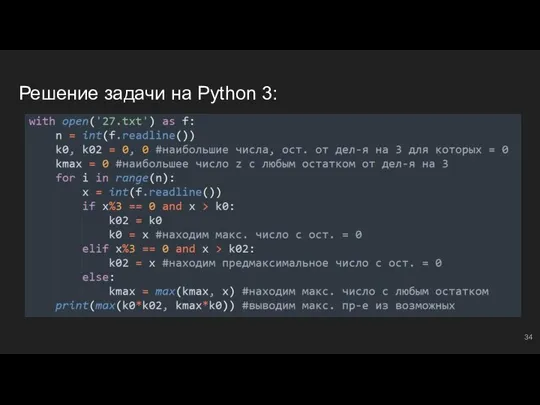
- 34. Решение задачи на Python 3:
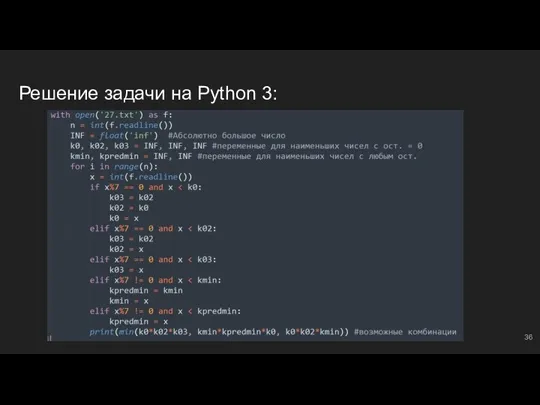
- 35. #2: №3 В файле ‘27.txt’ представлена последовательность N целых чисел. В первой строке находится число N,
- 36. Решение задачи на Python 3:
- 37. Обработка остатков #3: массивы В прошлом блоке разобрали базис “прямых” остатков. Как Вы поняли, существуют некие
- 38. Чем нам поможет массив в решении задач? Ранее было сказано, что массивы мы будем использовать для
- 39. Объявим массив ⇔ ⇔ Имеем массив размерности = z = 3. Не забываем, что индексация (нумерация)
- 40. Как обновлять информацию в массиве? Мы хотим найти наибольшее произведение двух элементов, кратное 3. Поэтому, в
- 41. Как мы в итоге получим ответ? Продолжаем рассматривать на примере всё той же задачи: OPltcm С
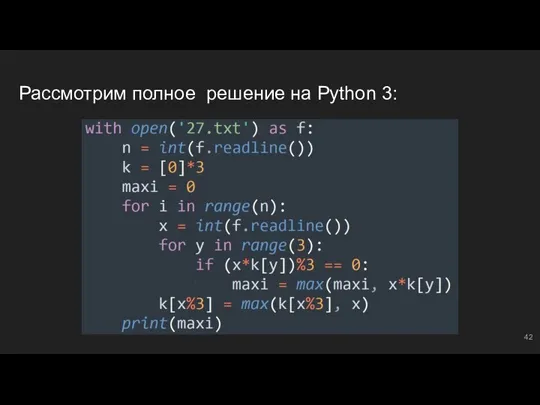
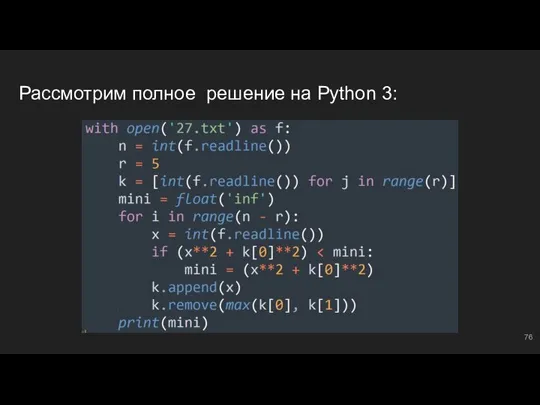
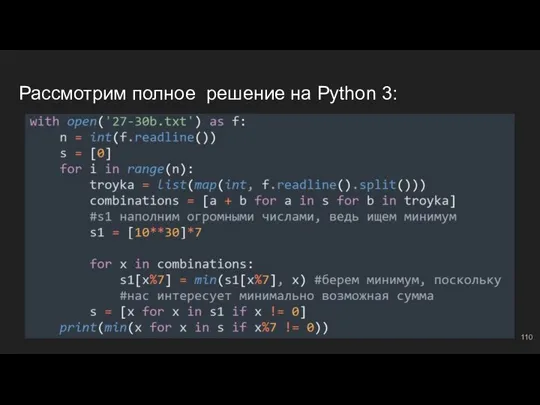
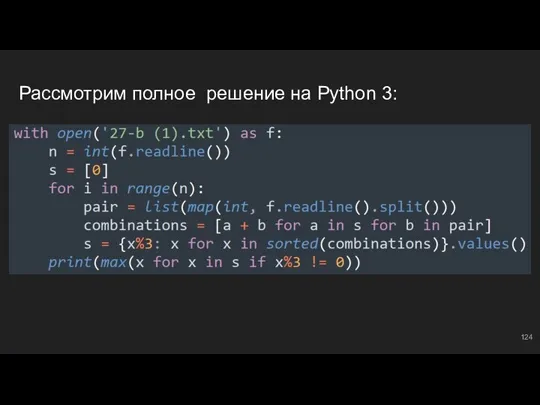
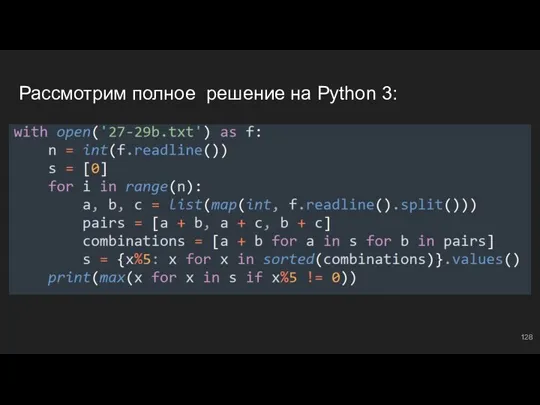
- 42. Рассмотрим полное решение на Python 3:
- 43. Обработка остатков #3: задачи средней сложности Решим легкие и средние задачи, связанные с делимостью и остатками,
- 44. #3: №1 В файле ‘27.txt’ представлена последовательность N целых чисел. В первой строке находится число N,
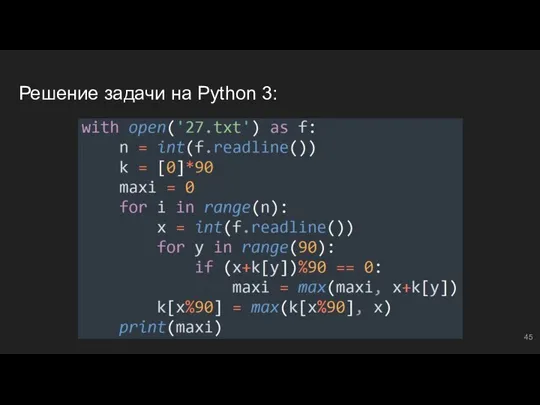
- 45. Решение задачи на Python 3:
- 46. #3: №2 В файле ‘27.txt’ представлена последовательность N целых чисел. В первой строке находится число N,
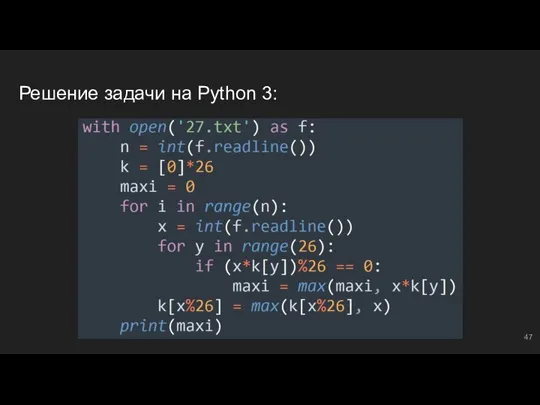
- 47. Решение задачи на Python 3:
- 48. #3: №3 В файле ‘27.txt’ представлена последовательность N целых чисел. В первой строке находится число N,
- 49. Решение задачи на Python 3:
- 50. Работа с делимостью #4: “дополняющие” остатки В блоке #2 разобрались с “прямыми” остатками. В этом же
- 51. Как работают “дополняющие” остатки? Предположим, есть ситуация, в ходе которой мы утверждаем, что выражение: (x +
- 52. Рассмотрим на других примерах Какой остаток от деления на 3 должен иметь y, чтобы (x +
- 53. Формула “дополняющего” остатка Выведем формулу дополняющего остатка. Пусть интересующий остаток = ост.(у); число, которое нужно дополнить
- 54. Работа с делимостью #4: практика - задачи Решим легкие и средние задачи, связанные с делимостью и
- 55. #4: №1 В файле ‘27.txt’ представлена последовательность N целых чисел. В первой строке находится число N,
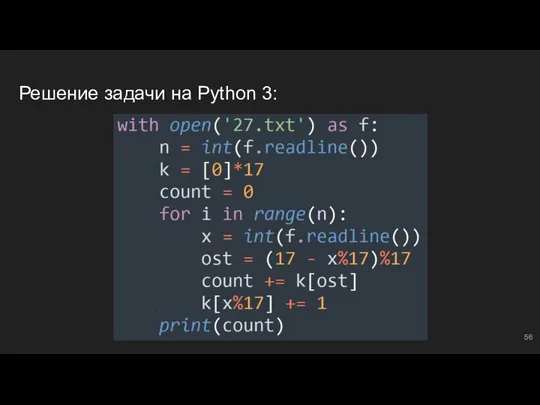
- 56. Решение задачи на Python 3:
- 57. #4: №2 В файле ‘27.txt’ представлена последовательность N целых чисел. В первой строке находится число N,
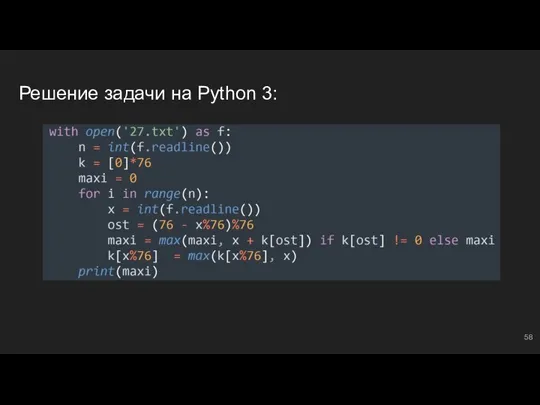
- 58. Решение задачи на Python 3:
- 59. #4: №3 В файле ‘27.txt’ представлена последовательность N целых чисел. В первой строке находится число N,
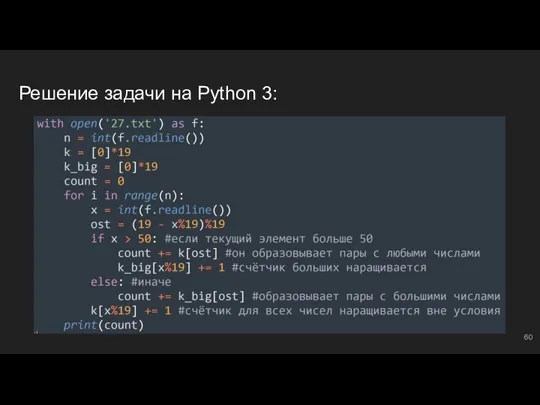
- 60. Решение задачи на Python 3:
- 61. Практика #5: решаем разные задачи В блоках #1 - #4 разобрались с делимостью, различными видами остатков,
- 62. #5: №1 Пробуем решить! Подсказки: Признаком окончания ввода является 0 - обратите внимание k = [0]*49
- 63. Решение задачи на Python 3: Открываем файл, задаем массив размерности z = 49, переменную maxi, в
- 64. #5: №2 Пробуем решить! Подсказки: k = [0]*26; храним количество чисел по остаткам, а не максимумы
- 65. Решение задачи на Python 3: Открываем файл, задаем массив размерности z = 26, переменную count, в
- 66. #5: №3 Пробуем решить! Подсказки: k = [0]*80; храним количество всех чисел пар по остаткам count
- 67. Решение задачи на Python 3: Открываем файл, задаем массив размерности z = 80, переменную count, в
- 68. #5: №4 Пробуем решить! Подсказки: k = [0]*14; храним наибольшие числа по остаткам maxi = 0;
- 69. Решение задачи на Python 3: Открываем файл, задаем массив размерности z = 14, переменную maxi, в
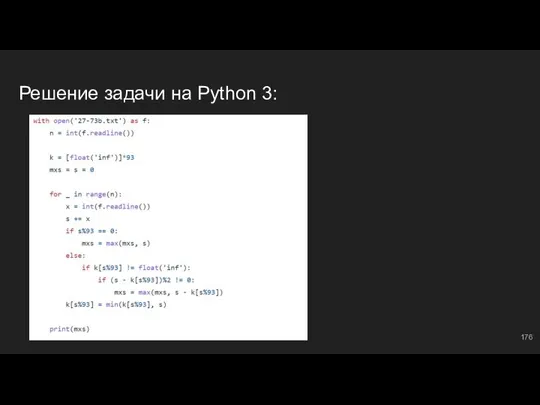
- 70. #5: №5 Что-то новенькое… Нужно учитывать расстояние (интервал не менее чем в 5 минут), это же
- 71. Расстояние #6: работа с “буфером” В предыдущем, #5 блоке, встретились с новым типом задач, которые предполагают
- 72. Какой еще “буфер” ? Вы, возможно, знаете, что такое буфер обмена, - промежуточное хранилище данных, которое
- 73. Создаем так называемый буфер Задача: найти наименьшую сумму квадратов чисел, расположенных на расстоянии не менее 5
- 74. Обрабатываем буферную информацию Как теперь обработать буфер в соответствии с условием задачи? Проходясь по циклу, если
- 75. Обновляем буферную информацию Теперь нужно обновить наш буфер, добавив в него новое число, которое мы считали.
- 76. Рассмотрим полное решение на Python 3:
- 77. Расстояние #6: практика - задачи Решим легкие и средние задачи, связанные с делимостью, остатками и расстоянием,
- 78. #6: №1 Рассуждаем: Буферизуем: r = 6 ⇔ k = [int(f.readline()) for j in range(r)] Не
- 79. Решение задачи на Python 3:
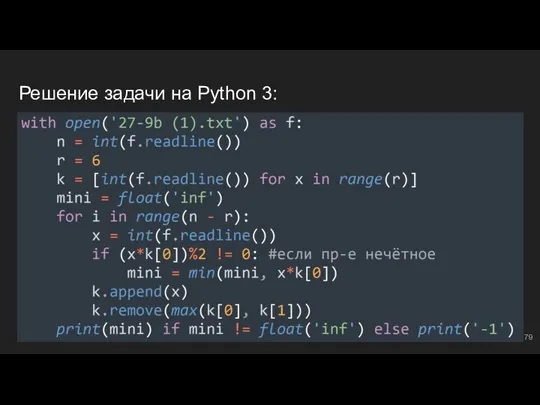
- 80. #6: №2 Используем всё, чему научились: Буферизуем: r = 5 ⇔ read = [int(f.readline()) for j
- 81. Решение задачи на Python 3: Открываем файл, задаем массив размерности z = 14, переменную count, в
- 82. Пары чисел #7: метод “минимальной разности” Начинаем разбирать задачи на пары чисел (два ряда чисел в
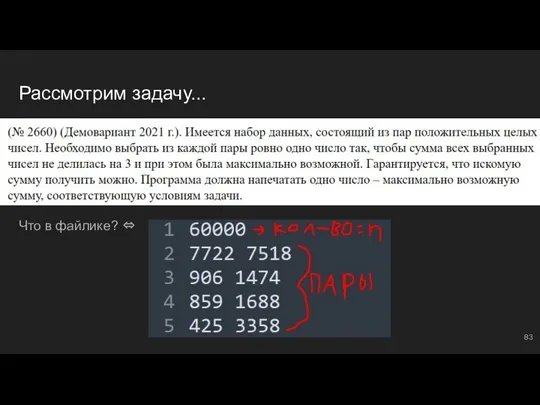
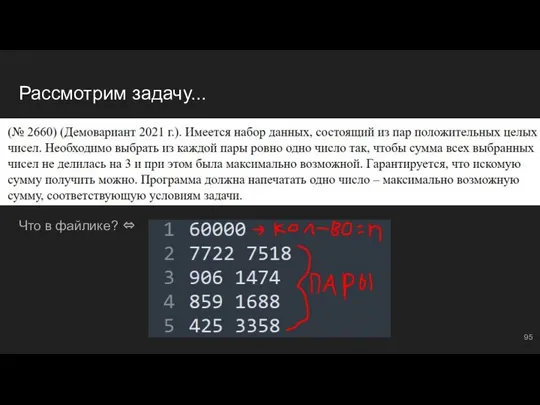
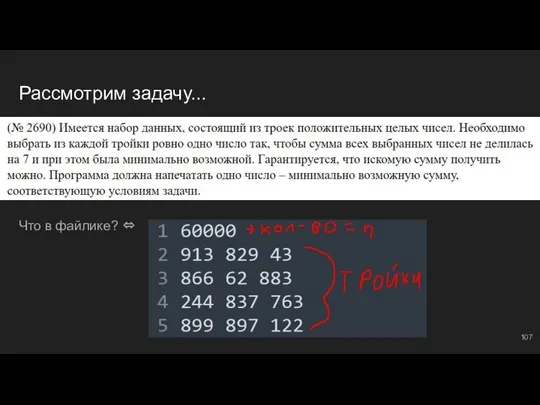
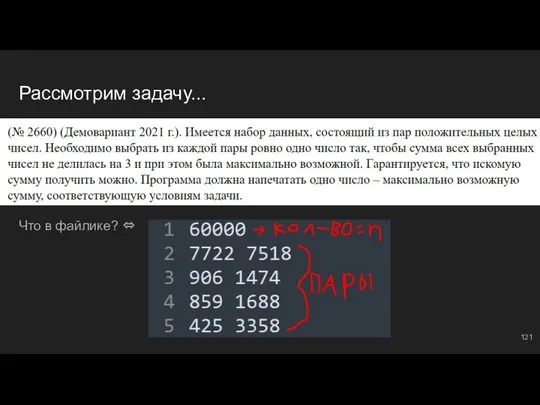
- 83. Рассмотрим задачу... Что в файлике? ⇔
- 84. Пробуем решить Как прочитать пару чисел в строке? (вдруг кто забыл): Здесь split() ⇔ разделение по
- 85. Получаем максимальную сумму Чтобы получить наибольшую сумму, выбрав из каждой пары ровно одно число, будем выбирать
- 86. Подгоняем сумму до ответа На помощь придет метод минимальной разности! Как мы уже выяснили, в какой-то
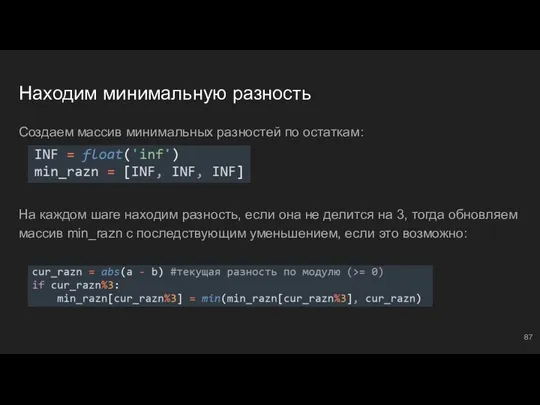
- 87. Находим минимальную разность Создаем массив минимальных разностей по остаткам: На каждом шаге находим разность, если она
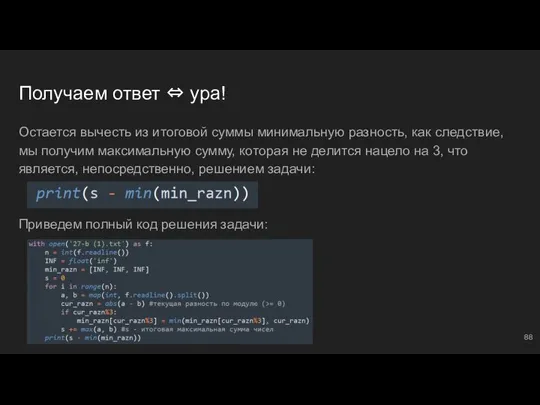
- 88. Получаем ответ ⇔ ура! Остается вычесть из итоговой суммы минимальную разность, как следствие, мы получим максимальную
- 89. Чем плох метод “минимальной разности”? Если Вы поняли идею, значит, врубаетесь: мы меняем итоговую сумму, прибавляя
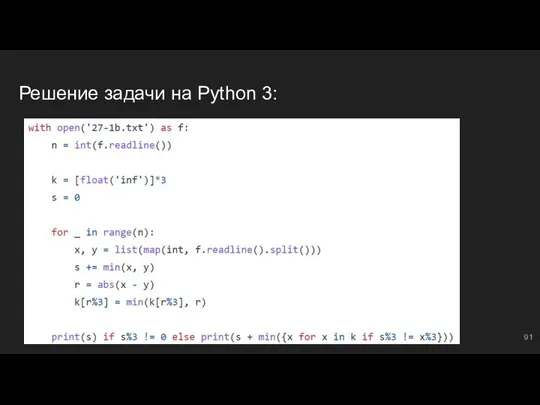
- 90. Пары чисел #7: решим задачу для закрепления темы Используем, что знаем: k = [float('inf')]*3 ⇔ массив
- 91. Решение задачи на Python 3:
- 92. Пары чисел #8: метод “частичных сумм” Начинаем разбирать задачи на пары чисел (два ряда чисел в
- 93. В чем состоит суть МЧС? Суть метода заключается в накоплении максимальных (или минимальных, в зависимости от
- 94. Рассмотрим МЧС на примере: Дан ряд из n = 2 пар чисел: Необходимо выбрать из каждой
- 95. Рассмотрим задачу... Что в файлике? ⇔
- 96. Пишем код для МЧС... Создадим буфер накопленных сумм ⇔ s = [0] for i in range(n):
- 97. Получаем результат В итоге в буфере s хранятся наибольшие суммы, которые удалось образовать, с соответствующими остатками.
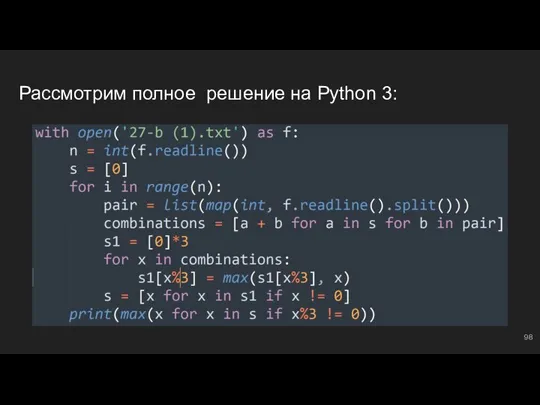
- 98. Рассмотрим полное решение на Python 3:
- 99. Пары чисел #8: практика - задачи Решим легкие и средние задачи, связанные с МЧС (методом “частичных
- 100. #8: №1 Создаем буфер ⇔ s = [0]; далее по классике - типичный метод частичных сумм.
- 101. Решение задачи на Python 3:
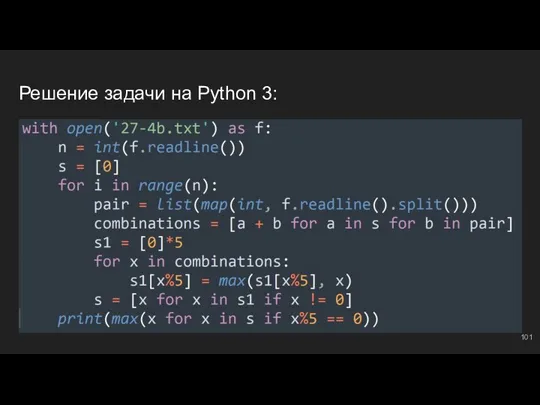
- 102. #8: №2 Создаем буфер ⇔ s = [0]; далее по классике - типичный метод частичных сумм.
- 103. Решение задачи на Python 3:
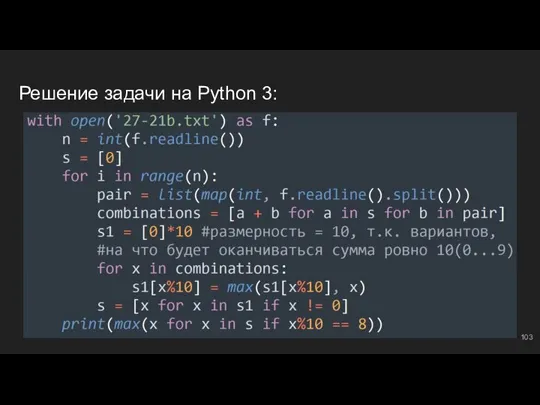
- 104. #8: №3 Создаем буфер ⇔ s = [0]; далее по классике - типичный метод частичных сумм.
- 105. Решение задачи на Python 3:
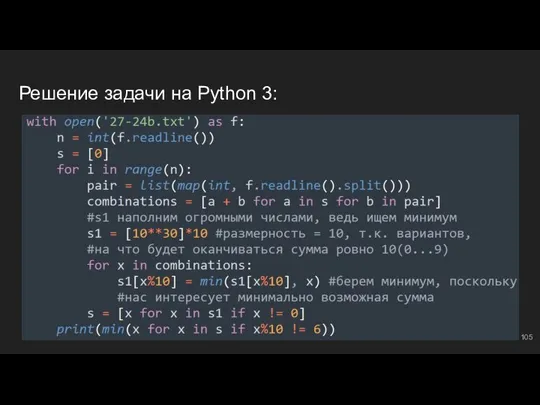
- 106. Тройки чисел #9: метод “частичных сумм” Начинаем разбирать задачи на тройки чисел (три ряда чисел в
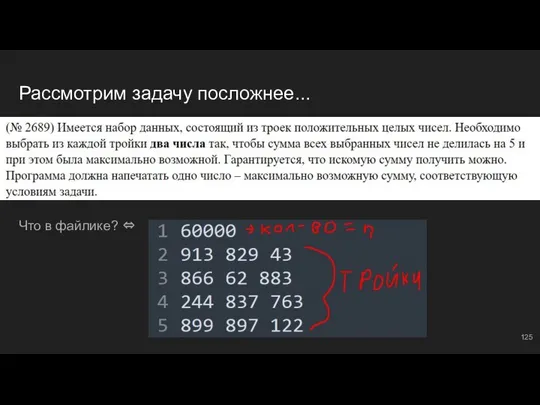
- 107. Рассмотрим задачу... Что в файлике? ⇔
- 108. Пишем код для МЧС... Создадим буфер накопленных сумм ⇔ s = [0] for i in range(n):
- 109. Получаем результат В итоге в буфере s хранятся наибольшие суммы, которые удалось образовать, с соответствующими остатками.
- 110. Рассмотрим полное решение на Python 3:
- 111. Рассмотрим задачу посложнее... Что в файлике? ⇔
- 112. Пишем код для МЧС... Создадим буфер накопленных сумм ⇔ s = [0] for i in range(n):
- 113. Получаем результат В итоге в буфере s хранятся наибольшие суммы, которые удалось образовать, с соответствующими остатками.
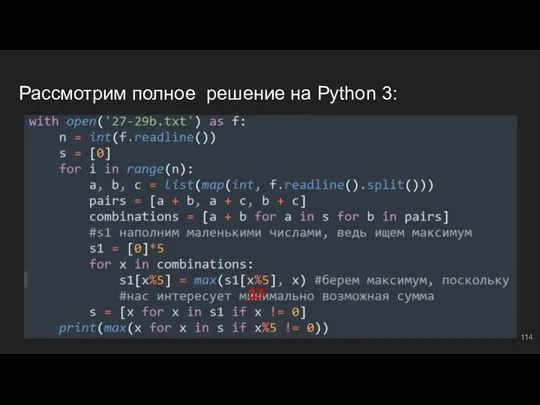
- 114. Рассмотрим полное решение на Python 3:
- 115. Тройки чисел #9: практика - задачи Решим легкие и средние задачи, связанные с МЧС (методом “частичных
- 116. #9: №1 Создаем буфер ⇔ s = [0]; далее по классике - типичный метод частичных сумм.
- 117. Решение задачи на Python 3:
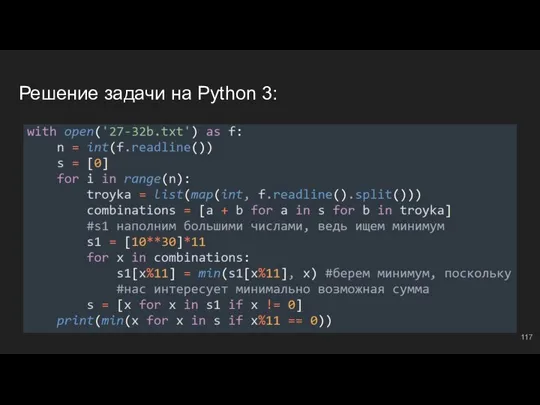
- 118. #9: №2 Создаем буфер ⇔ s = [0]; далее по классике - типичный метод частичных сумм.
- 119. Решение задачи на Python 3:
- 120. Тройки и пары #10: упрощаем МЧС Пришло время МЧС! В прошлых блоках разобрались, как он работает,
- 121. Рассмотрим задачу... Что в файлике? ⇔
- 122. Пишем короткий код для МЧС... Создадим буфер накопленных сумм ⇔ s = [0] for i in
- 123. Получаем результат В итоге в буфере s хранятся наибольшие суммы, которые удалось образовать, с соответствующими остатками.
- 124. Рассмотрим полное решение на Python 3:
- 125. Рассмотрим задачу посложнее... Что в файлике? ⇔
- 126. Пишем короткий код для МЧС... Создадим буфер накопленных сумм ⇔ s = [0] for i in
- 127. Получаем результат В итоге в буфере s хранятся наибольшие суммы, которые удалось образовать, с соответствующими остатками.
- 128. Рассмотрим полное решение на Python 3:
- 129. Тройки и пары #10: практика - задачи Решим легкие и средние задачи, связанные с упрощенным МЧС
- 130. #10: №1 Здесь, помимо основной суммы, найдем еще и минимально возможную, дабы сравнить остатки: mins ⇔
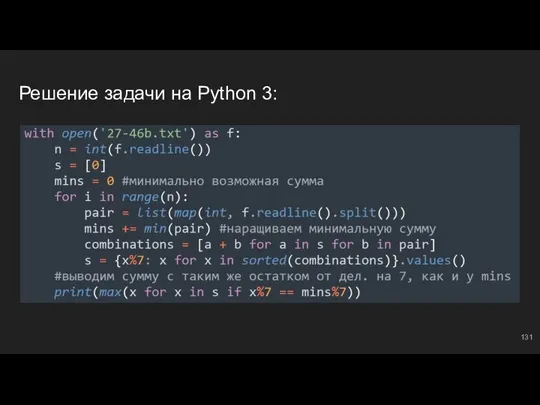
- 131. Решение задачи на Python 3:
- 132. #10: №2 Обратим внимание на то, что нас интересует минимально возможная сумма, значит, сортируем с переворотом
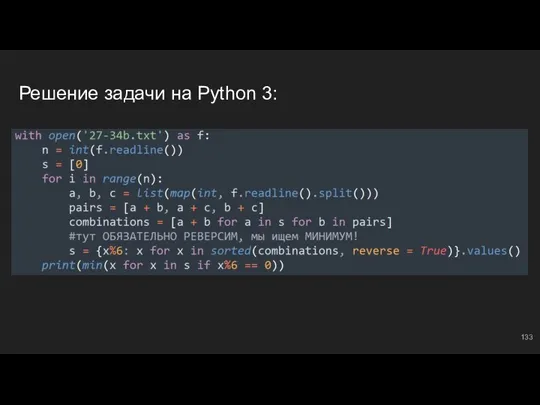
- 133. Решение задачи на Python 3:
- 134. #10: №3 Вспоминаем блоки #2 и #4, друзья! Чтобы сумма делилась на x и на y
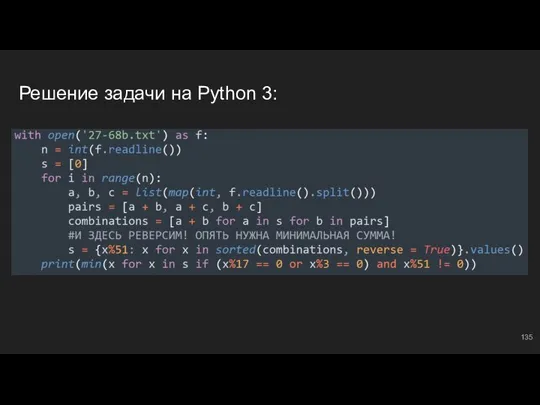
- 135. Решение задачи на Python 3:
- 136. Группы чисел #11: поиск количеств / сумм Ранее, в блоках #2 - #6 мы встречались с
- 137. Рассмотрим задачу... Как будем решать? Создаем массив по остаткам, в котором будем хранить количество чисел и
- 138. Как будем наращивать количество? for i in range(n): ⇔ проходимся по файлу x = int(f.readline()) ⇔
- 139. Рассмотрим полное решение на Python 3:
- 140. Рассмотрим задачу... Как будем решать? Создаем массив с максимальными суммами по остаткам: k = [0]*25 В
- 141. Как будем наращивать сумму? for i in range(n): ⇔ проходимся по файлу x = int(f.readline()) ⇔
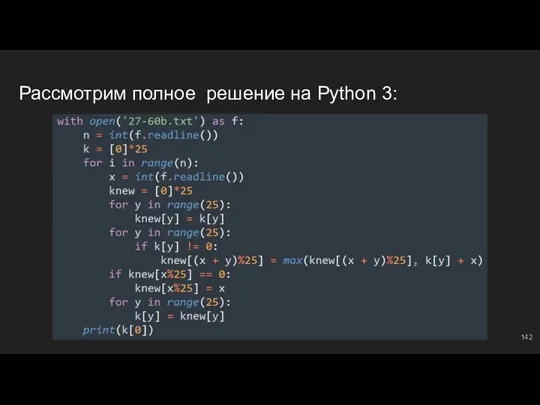
- 142. Рассмотрим полное решение на Python 3:
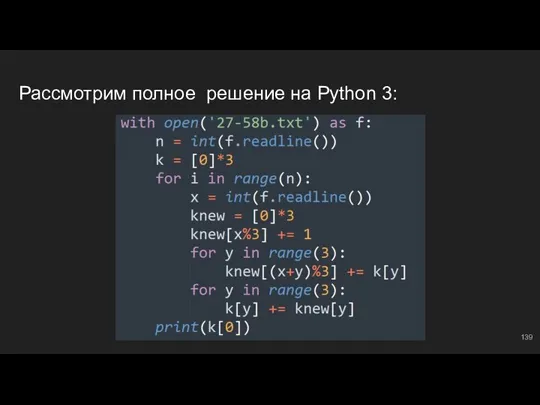
- 143. Группы чисел #11: практика - задачи Решим легкие и средние задачи, связанные с обработкой групп чисел
- 144. #11: №1 K k = [0]*10 ⇔ всего на 10 разных вариантов может оканчиваться сумма элементов:
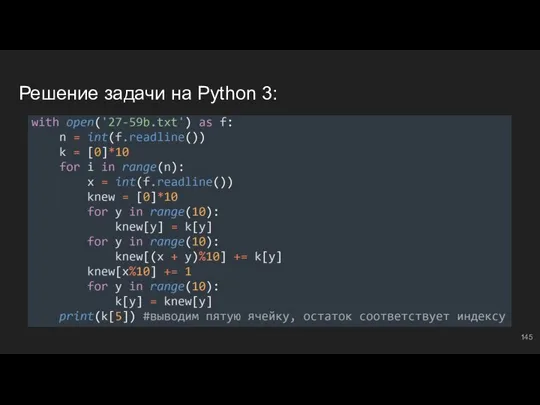
- 145. Решение задачи на Python 3:
- 146. #11: №2 K k = [0]*100 ⇔ всего на 100 разных вариантов может оканчиваться сумма элементов,
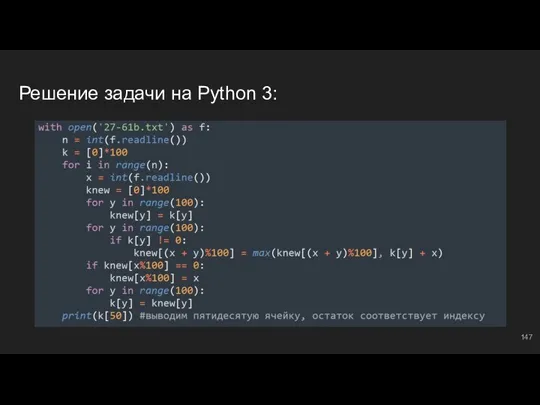
- 147. Решение задачи на Python 3:
- 148. Распределение по группам #12: остатки В этом блоке познакомимся с задачами, в которых нам даны два
- 149. Рассмотрим задачу... Как будем решать? Распределим все числа на три группы, при этом будем сохранять минимальные
- 150. Находим суммы в группах next(f) ⇔ пропускаем первое число в файле, оно нам не понадобится s1
- 151. Сохраняем минимальные разности if a[1]%2 != a[0]%2: ⇔ если элементы с разными остатками k.append([(a[1] - a[0]),
- 152. Вычитаем до соответствия n = 0 ⇔ счетчик элементов в списке (индексатор) while True: ⇔ пока
- 153. Рассмотрим полное решение на Python 3:
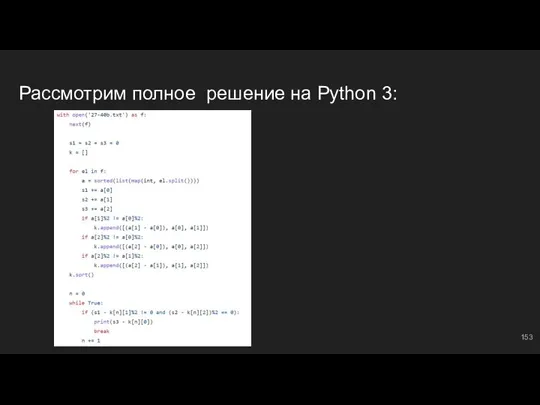
- 154. Рассмотрим еще одну задачу... Как будем решать? Будем сохранять всякие разности по остаткам, которые в конечном
- 155. Накапливаем сумму k = [0]*2 ⇔ количество чет. / нечет. mini = [] ⇔ список разностей
- 156. Учитываем четность, находим разности На каждой итерации по циклу подсчитываем количество четных и нечетных выбранных максимальных
- 157. Рассмотрим полное решение на Python 3:
- 158. Распределение по группам #12: практика - задачи Решим легкие и средние задачи, связанные с обработкой групп
- 159. #12: №1 K Ровно та же логика: ищем по остаткам непохожие минимальные разности, после чего по
- 160. Решение задачи на Python 3:
- 161. #12: №2 K Ровно та же логика: высчитываем четность большинства выбранных элементов, если четность итоговой суммы
- 162. Решение задачи на Python 3:
- 163. Подпоследовательности #13: длины / суммы В этом блоке познакомимся с задачами, в которых нам дана последовательность
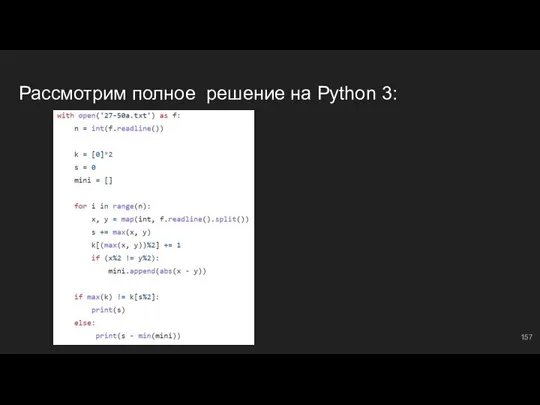
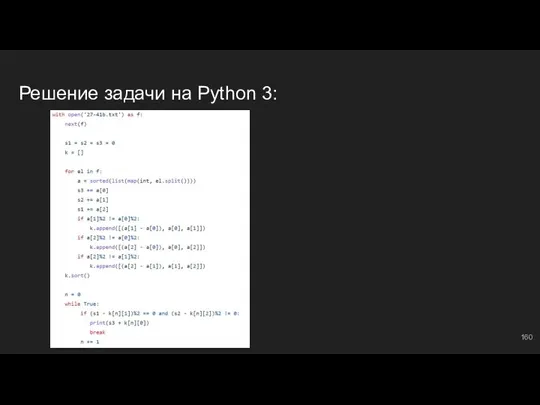
- 164. Рассмотрим задачу... Как будем решать? МАССИВЫ - МОЩЬ! Заведем соответствующие по индексам массивы, отвечающие за разные
- 165. Накапливаем сумму maxs = 0 ⇔ максимальная сумма, кратная 43 minl = float(‘inf’) ⇔ минимальная длина
- 166. Обрабатываем массивы Идея: мы будем находить минимальные суммы идущих подряд чисел с разными остатками от деления
- 167. Обновляем макс. сумму и ее длину На каждой итерации цикла: if prefs[ost] != 0: ⇔ если
- 168. Дорешиваем до конца Не забываем обрабатывать исключительный случай, когда сумма на данном этапе уже кратна 43:
- 169. Рассмотрим полное решение на Python 3:
- 170. Рассмотрим еще одну задачу... Как будем решать? МАССИВЫ - МОЩЬ! Заведем массив, который будет отвечать за
- 171. Обрабатываем массив for i in range(n): ⇔ проходимся по файлику x = int(f.readline()) ⇔ читаем число
- 172. Дорешиваем до конца if s%71 == 0: ⇔ если текущая сумма кратна 71 count += 1
- 173. Рассмотрим полное решение на Python 3:
- 174. Подпоследовательности #13: практика - задачи Решим легкие и средние задачи, связанные с обработкой непрерывных подпоследовательностей по
- 175. #13: №1 K Ровно та же логика, что и в прошлых задачах - друзья массивы! Создаем
- 176. Решение задачи на Python 3:
- 177. #13: №2 K Ровно та же логика, что и в прошлых задачах - друзья массивы! Создаем
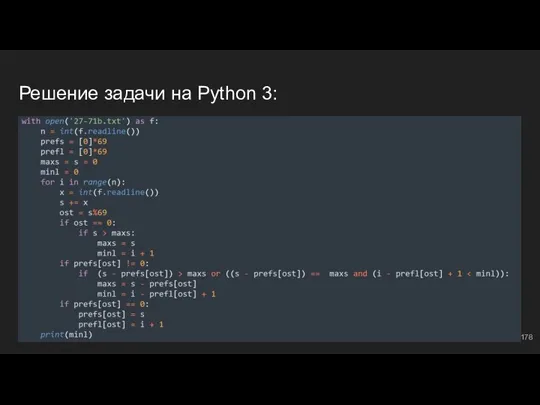
- 178. Решение задачи на Python 3:
- 179. Переборные алгоритмы #14: вложенные циклы В этом блоке разберемся, как решать задачи переборно (неэффективно), переборным алгоритмом
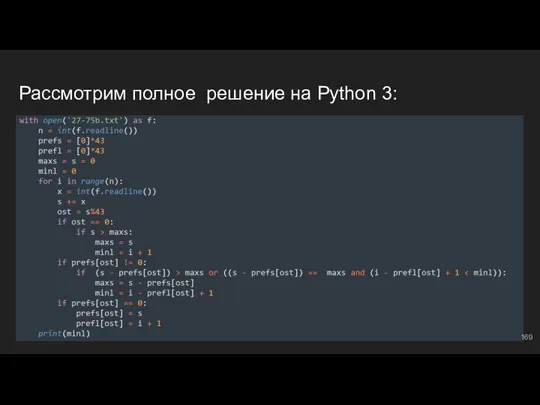
- 180. Рассмотрим на примере: a = [3, 5, 7, 11] ⇔ список из 4 чисел n =
- 181. Какие значения будут принимать i, j? На выводе имеем: i, j - итераторы цикла. Вы точно
- 182. Что будет выведено? i, j = 0, 1 ⇔ a[i] = 3, a[j] = 5 ⇔
- 183. Рассмотрим задачу... Как будем решать? Сейчас решим задачу переборно, с использованием вложенных циклов, решение сработает только
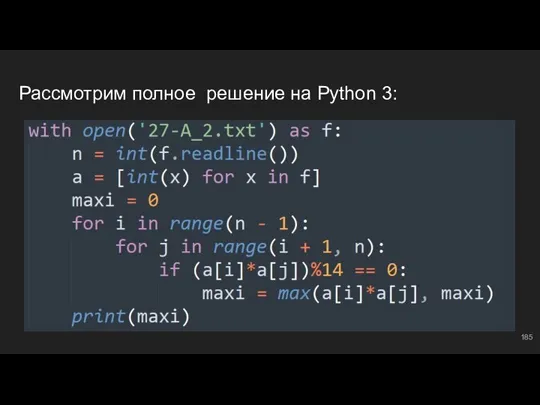
- 184. Перебираем все произведения for i in range(n - 1): ⇔ для каждого элемента с индексом i
- 185. Рассмотрим полное решение на Python 3:
- 186. Переборные алгоритмы #14: практика - задачи Решим легкие и средние задачи, связанные с обработкой непрерывных подпоследовательностей
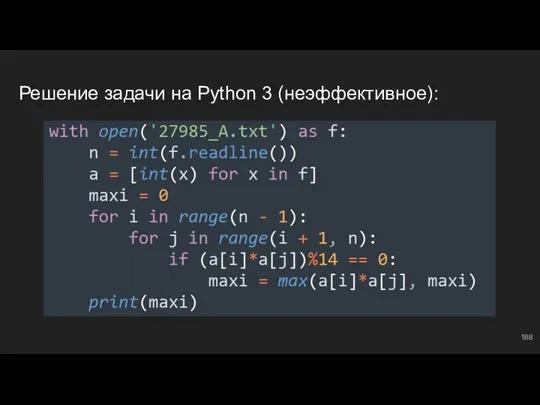
- 187. #14: №1 K Пробуйте свои силы, на следующем слайде будет представлено решение.
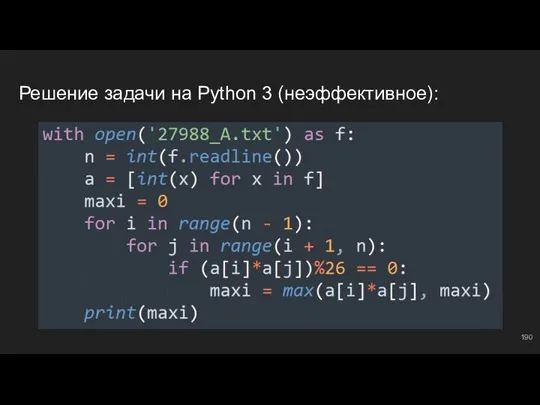
- 188. Решение задачи на Python 3 (неэффективное):
- 189. #14: №1 Здесь Вы, наверное, ждете какой-то подсказки, но я не знаю, что можно придумать)))) Все
- 190. Решение задачи на Python 3 (неэффективное):
- 191. Бонусный блок #15: экзотика (задачи и решения) В этом блоке разберем некоторые экзотические задачи. Важно понимать,
- 192. #15: №1 Начнем мы с наиболее простых задач. В некотором смысле их даже нельзя отнести к
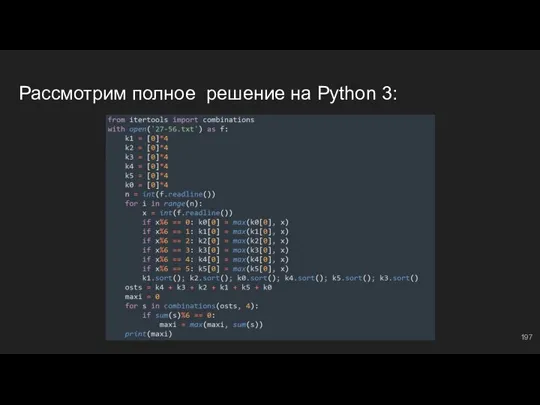
- 193. Itertools, combinations... Вы, очевидно, знаете, что такое combinations (permutations и product из той же серии). Чаще
- 194. Создаем массивы по остаткам Говорилось уже, массивы - друзья наши: k1 = [0]*4 ⇔ 4 числа
- 195. Ищем наибольшие числа Проходясь по циклу, читая число (всё это вы уже умеете давно): if x%6
- 196. Комбинируем! Теперь мы будем рассматривать всевозможные комбинации, состоящие из четырех чисел (образовываться они будут путем перестановок
- 197. Рассмотрим полное решение на Python 3:
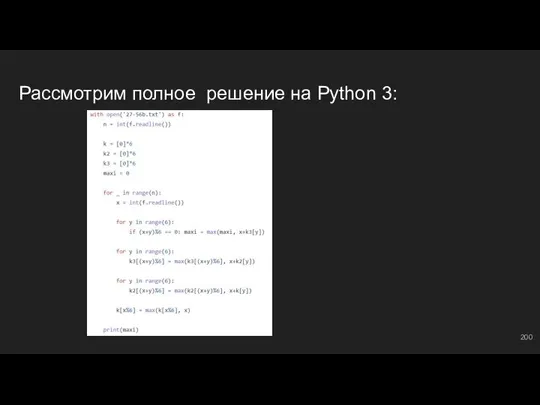
- 198. Решим эту же задачу классически k = [0]*6 ⇔ массив наибольших чисел с разными остатками k2
- 199. Обновляем массивы сумм for y in range(6): ⇔ проходимся по разным остаткам k2[(x+y)%6] = max(k2[(x+y)%6], x+k[y])
- 200. Рассмотрим полное решение на Python 3:
- 201. #15: №2 Легкая задача, можно связать с обработкой последовательности целых чисел, обработкой подпоследовательностей. Но, к экзотике
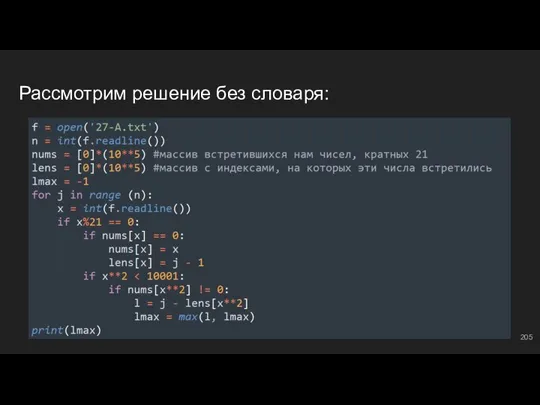
- 202. Как будем решать? one = set() ⇔ создаем множество, в нем будем хранить все числа, кратные
- 203. Обрабатываем словарь и множество if x%21 == 0: ⇔ если текущий х делится на 21 if
- 204. Рассмотрим полное решение на Python 3:
- 205. Рассмотрим решение без словаря:
- 206. #15: №3 В этой задаче тоже мало сложного, здесь сработает типичный МЧС, просто нужно как-то обрабатывать
- 207. Как будем решать? Очевидно, воспользуемся типичным МЧС для нахождения суммы чисел. Одно “но”: нужно создавать комбинации
- 208. Наращиваем сумму k = {0} ⇔ храним здесь наши суммы (всп. блоки #8-10) for i in
- 209. Рассмотрим полное решение на Python 3:
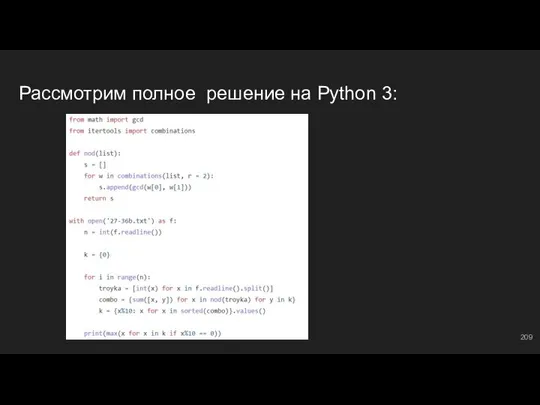
- 210. #15: №4 Эта задача очень похожа на предыдущую, но здесь нам нужно находить НОК чисел, при
- 211. Импортируем библиотеки from itertools import combinations as cmb ⇔ импортируем комбинейшнс (будем комбинировать по 2 числа
- 212. Пишем функцию для поиска НОК def nok(set): return reduce(lambda x, y: x*y//gcd(x, y), set) В функцию
- 213. Наращиваем сумму k = {0} ⇔ здесь храним наши суммы по остаткам for i in range(n):
- 214. Получаем результат Остается только выводить результат. У кого-нибудь возник вопрос, почему мы сортируем по остаткам от
- 215. Рассмотрим полное решение на Python 3:
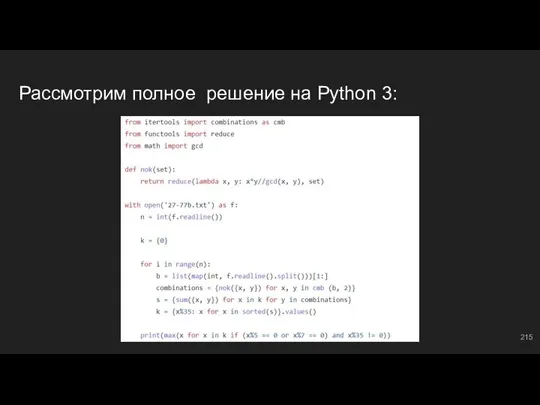
- 216. #15: №5 Задача на логику и соображалку. Крайне легкая, если разобраться. Отлично подойдет в качестве на
- 217. В чем идея решения? В файле находятся различные числа, в том числе и отрицательные и нули.
- 218. Рассмотрим полное решение на Python 3:
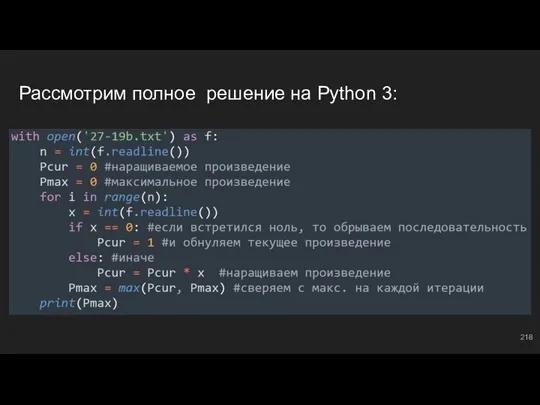
- 219. #15: №6 Ровно как и предыдущая, эта задача тоже на логику и соображалку. И вновь помогут
- 220. В чем идея решения? Мы заведем два массива по остаткам от деления на 2, вспоминаете блоки
- 221. Обрабатываем массивы if x == 0: ⇔ если встретился ноль, значит K0 = Kall.copy() ⇔ в
- 222. Рассмотрим полное решение на Python 3:
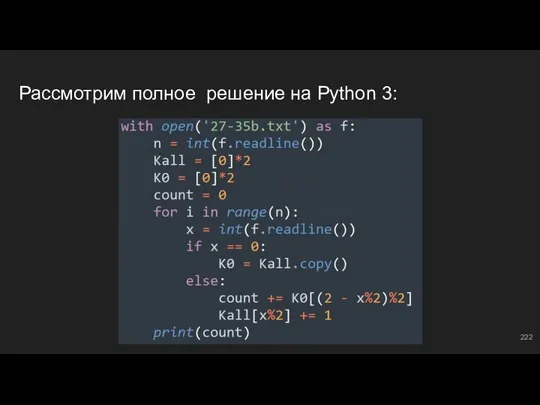
- 223. #15: №7 В блоках #7 - #10 мы познакомились с МЧС (методом частичных сумм). Теперь предлагаю
- 224. В чем идея решения? Мы будем использовать массив, который хранит в себе два аргумента: первый аргумент
- 225. Обрабатываем массив combinations = [[a + x, b + 1] for a, b in k] +
- 226. Обновляем результат На каждой итерации проходимся по k, здесь s - сумма, l - длина. Далее:
- 227. Почему решение эффективно? Возможно, вы задались таким вопросом, ведь в каждой итерации мы проходимся по k.
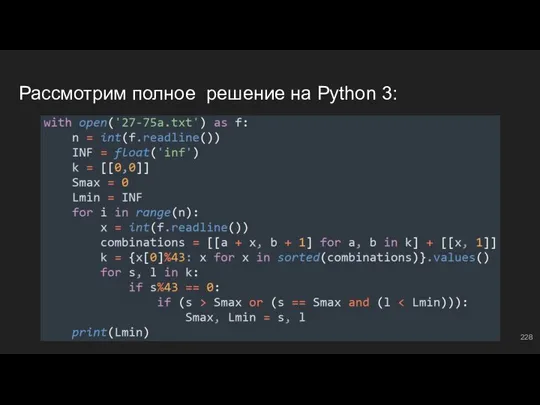
- 228. Рассмотрим полное решение на Python 3:
- 229. #15: №8 На первый взгляд - гроб, не правда ли? Эта задача является усложненной версией задачи
- 230. В чем идея решения? Ровно та же идея, массив, хранящий два элемента: сумму и количество элементов
- 231. Обновляем результат На каждой итерации проходимся по k: for a, b in k: ⇔ для суммы,
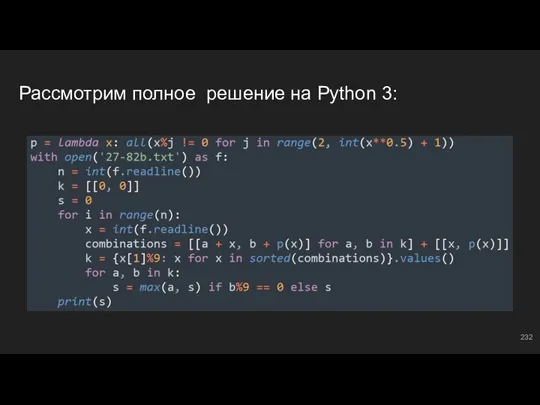
- 232. Рассмотрим полное решение на Python 3:
- 233. #15: №9 Задача, в которой нам придется обрабатывать геометрические прогрессии на каждой итерации. Есть два способа
- 234. Рассмотрим пример для этой задачи Пример входного файла: 5 4 216 36 6 1 7 128
- 235. В чем идея решения? Нам нужно находить геометрические прогрессии. При этом, внимательно читаем условие задачи, мы
- 236. Находим прогрессии с наибольшей суммой def gprog(list): ⇔ функция поиска наибольшей геом. прогрессии (передаем в нее
- 237. Обрабатываем группы чисел next(f) ⇔ пропускаем первое число (кол-во чисел), оно нам не пригодится s =
- 238. Как найти минимальные разности? Уже на данном этапе мы имеем максимальную сумму, которую только возможно найти,
- 239. Находим минимальные разности saveost = {0} ⇔ храним тут минимальные разности по остаткам, далее, с каждой
- 240. Получаем результат На текущем моменте в saveost мы имеем множество разностей с различными остатками. Теперь, чтобы
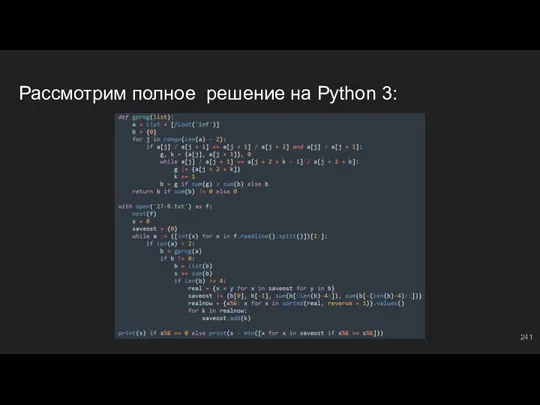
- 241. Рассмотрим полное решение на Python 3:
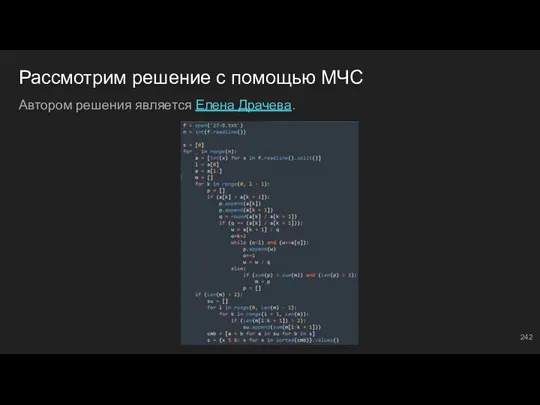
- 242. Рассмотрим решение с помощью МЧС Автором решения является Елена Драчева.
- 243. #15: №10 Гроб, ровно как и прошлая задача, но гроб решаемый. Здесь нам помогут наши друзья-массивы,
- 244. В чем идея решения? Нас интересует, чтобы сумма делилась на 3, в то же время, чтобы
- 245. Обрабатываем массивы xfirst = int(f.readline()) ⇔ читаем первое число вне цикла, далее, проходясь по циклу: xnext
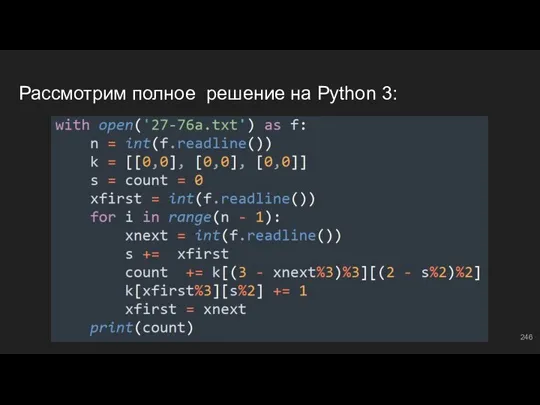
- 246. Рассмотрим полное решение на Python 3:
- 247. Как решить неэффективно? Порой сложно придумать эффективное решение для подобных задач, но один балл все-таки забрать
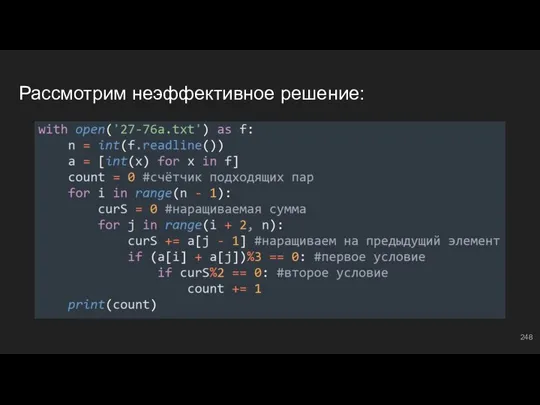
- 248. Рассмотрим неэффективное решение:
- 249. Рекомендации Данный материал будет полезен как школьникам, сдающим КЕГЭ, так и преподавателям. Разобраны различные виды 27-х
- 250. Список использованных источников Источники задач: https://kpolyakov.spb.ru/ - сайт К.Ю. Полякова https://rus-ege.sdamgia.ru/ - сайт Решу ЕГЭ https://kompege.ru/
- 252. Скачать презентацию












































![#5: №1 Пробуем решить! Подсказки: Признаком окончания ввода является 0 - обратите внимание k = [0]*49](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/992322/slide-61.jpg)

![#5: №2 Пробуем решить! Подсказки: k = [0]*26; храним количество чисел по](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/992322/slide-63.jpg)

![#5: №3 Пробуем решить! Подсказки: k = [0]*80; храним количество всех чисел](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/992322/slide-65.jpg)

![#5: №4 Пробуем решить! Подсказки: k = [0]*14; храним наибольшие числа по](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/992322/slide-67.jpg)




















![Пишем код для МЧС... Создадим буфер накопленных сумм ⇔ s = [0]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/992322/slide-95.jpg)


![#8: №1 Создаем буфер ⇔ s = [0]; далее по классике -](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/992322/slide-99.jpg)
![#8: №2 Создаем буфер ⇔ s = [0]; далее по классике -](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/992322/slide-101.jpg)
![#8: №3 Создаем буфер ⇔ s = [0]; далее по классике -](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/992322/slide-103.jpg)

![Пишем код для МЧС... Создадим буфер накопленных сумм ⇔ s = [0]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/992322/slide-107.jpg)

![Пишем код для МЧС... Создадим буфер накопленных сумм ⇔ s = [0]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/992322/slide-111.jpg)


![#9: №1 Создаем буфер ⇔ s = [0]; далее по классике -](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/992322/slide-115.jpg)
![#9: №2 Создаем буфер ⇔ s = [0]; далее по классике -](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/992322/slide-117.jpg)















![#11: №1 K k = [0]*10 ⇔ всего на 10 разных вариантов](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/992322/slide-143.jpg)
![#11: №2 K k = [0]*100 ⇔ всего на 100 разных вариантов](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/992322/slide-145.jpg)



![Сохраняем минимальные разности if a[1]%2 != a[0]%2: ⇔ если элементы с разными](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/992322/slide-150.jpg)


![Накапливаем сумму k = [0]*2 ⇔ количество чет. / нечет. mini =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/992322/slide-154.jpg)









![Обновляем макс. сумму и ее длину На каждой итерации цикла: if prefs[ost]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/992322/slide-166.jpg)









![Рассмотрим на примере: a = [3, 5, 7, 11] ⇔ список из](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/992322/slide-179.jpg)

![Что будет выведено? i, j = 0, 1 ⇔ a[i] = 3,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/992322/slide-181.jpg)











![Решим эту же задачу классически k = [0]*6 ⇔ массив наибольших чисел](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/992322/slide-197.jpg)




















![Обрабатываем массив combinations = [[a + x, b + 1] for a,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/992322/slide-224.jpg)



















 Зеленый хайп. Что ждет экожурналистов
Зеленый хайп. Что ждет экожурналистов Программирование специализированных вычислительных устройств
Программирование специализированных вычислительных устройств Поколения ЭВМ
Поколения ЭВМ Интернет-ресурсы. Подготовка к ЕГЭ
Интернет-ресурсы. Подготовка к ЕГЭ Реляционные отношения между таблицами базы данных
Реляционные отношения между таблицами базы данных download (1)
download (1) HTML – язык разметки гипертекста
HTML – язык разметки гипертекста Школьный портал
Школьный портал Документ, его характеристики (формуляр, структура, юридическая сила, вид) и функции. Связь информации и документа
Документ, его характеристики (формуляр, структура, юридическая сила, вид) и функции. Связь информации и документа Программное обеспечение компьютера
Программное обеспечение компьютера никлаус вирт
никлаус вирт Автоматизация деятельности школьной библиотеки
Автоматизация деятельности школьной библиотеки 6
6 Tunel
Tunel Мобильное приложение Answers
Мобильное приложение Answers Информация и её свойства. Информация и информационные процессы
Информация и её свойства. Информация и информационные процессы Конструкция switch
Конструкция switch Индикатор Relative Strength Index
Индикатор Relative Strength Index Знакомство с устройствами компьютера и их назначением
Знакомство с устройствами компьютера и их назначением Циклы for , while, do while, а также команды continue и break
Циклы for , while, do while, а также команды continue и break Редактор таблиц GNUmeric
Редактор таблиц GNUmeric Информационная культура
Информационная культура Разборы задач №2. Системы счисления
Разборы задач №2. Системы счисления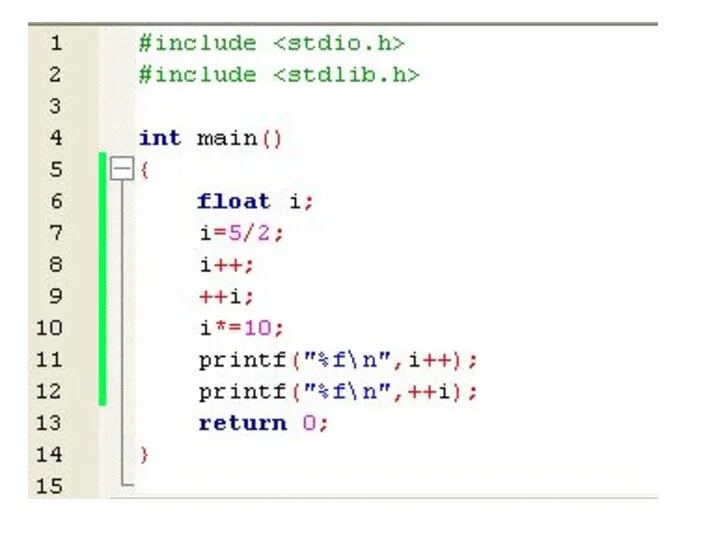 Code Bloks - среда программирования на языке C/C++. Результаты работы
Code Bloks - среда программирования на языке C/C++. Результаты работы Это Android
Это Android ВКонтакте
ВКонтакте Компилятор логико-алгебраических выражений для многомодульных систем
Компилятор логико-алгебраических выражений для многомодульных систем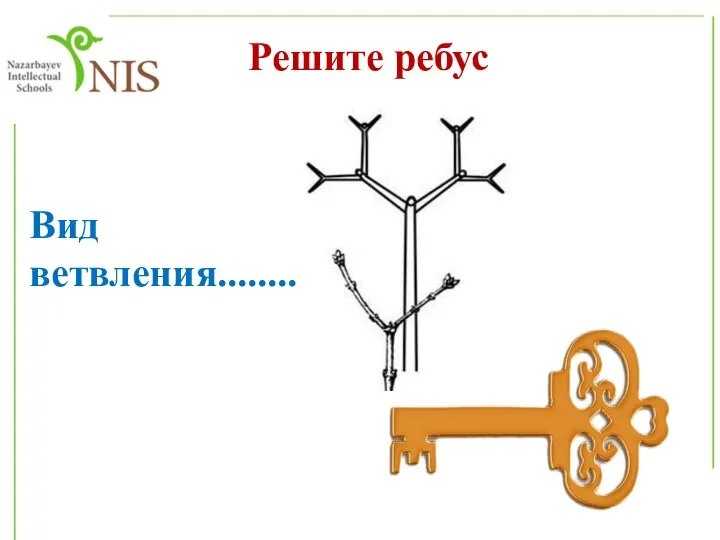 Дихотомический метод. Дихотомический ключ
Дихотомический метод. Дихотомический ключ