Слайд 2Задача RMQ
Range Minimum (Maximum) Query
Static & dynamic, offline & online
Предподсчёт

Слайд 3Решение RMQ через Sparse table
Sparse Table – это таблица ST[][] такая, что
![Решение RMQ через Sparse table Sparse Table – это таблица ST[][] такая,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/969447/slide-2.jpg)
ST[k][i] есть минимум на полуинтервале [A[i], A[i+2^k]).
Слайд 4Решение RMQ через дерево отрезков
Строим дерево отрезков
Фундаментальный отрезок -- полностью лежит

в поддереве какой-то вершины
За указатель l -- если мы находимся в правом поддереве, то обновляем результат, поднимаемся и перескакиваем на своего правого соседа на уровне. Если находимся в левом поддереве -- просто поднимаемся и обновляем.
За указатель r -- если мы находимся в левом поддереве, то --\--
online
Слайд 5LCA. Метод двоичного подъёма
Наименьший общий предок двух вершин
dp[v][i] — номер вершины, в
![LCA. Метод двоичного подъёма Наименьший общий предок двух вершин dp[v][i] — номер](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/969447/slide-4.jpg)
которую мы придём если пройдём из вершины v вверх по подвешенному дереву 2^i шагов, причём если мы пришли в корень, то мы там и останемся.

![Решение RMQ через Sparse table Sparse Table – это таблица ST[][] такая,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/969447/slide-2.jpg)

![LCA. Метод двоичного подъёма Наименьший общий предок двух вершин dp[v][i] — номер](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/969447/slide-4.jpg)

 Что такое код?
Что такое код? Файловый ввод и вывод
Файловый ввод и вывод Циклы в алгоритмах
Циклы в алгоритмах Dreamtrips без границ
Dreamtrips без границ Угрозы безопасности и методы защиты информации в общественных организациях
Угрозы безопасности и методы защиты информации в общественных организациях nestandartnye_programmnye_sposoby_postroenia_3d_modeley
nestandartnye_programmnye_sposoby_postroenia_3d_modeley Оперативная память Ram и Rom
Оперативная память Ram и Rom Компьютерно-опосредованный дискурс
Компьютерно-опосредованный дискурс Кто считается отцом виртуальной реальности?
Кто считается отцом виртуальной реальности? Знакомство с новой лексикой
Знакомство с новой лексикой Протоколы сети Интернет. Протокол POP3
Протоколы сети Интернет. Протокол POP3 Информирование сети об изменениях в стандартах
Информирование сети об изменениях в стандартах Язык программирования Pascal. Автомат
Язык программирования Pascal. Автомат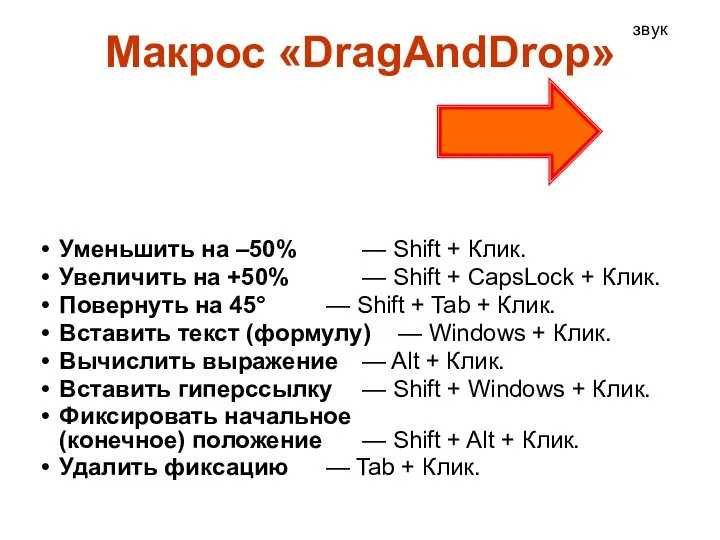 Макрос DragAndDrop
Макрос DragAndDrop 12_Строки
12_Строки Обработка информации. Практическая работа
Обработка информации. Практическая работа Викторина. Информационная безопасность и защита персональных данных
Викторина. Информационная безопасность и защита персональных данных Сжатие рисунков в документах Microsost Office
Сжатие рисунков в документах Microsost Office Интро. Аналитик в IT
Интро. Аналитик в IT Безопасный интернет. Как избежать опасностей?
Безопасный интернет. Как избежать опасностей? Компьютерная графика. Представление о программных средах компьютерной графики и черчения
Компьютерная графика. Представление о программных средах компьютерной графики и черчения Модели и моделирование
Модели и моделирование Презентация на тему Геоинформационные системы в Интернете (ГИС)
Презентация на тему Геоинформационные системы в Интернете (ГИС)  Системы цветопередачи RGB, CMYK, HSB
Системы цветопередачи RGB, CMYK, HSB Проект: Библиотека без стен
Проект: Библиотека без стен Оценка качества программного обеспечения (SQuaRE). Модели качества систем и программных продуктов ГОСТ Р ИСО/МЭК 25010–2015
Оценка качества программного обеспечения (SQuaRE). Модели качества систем и программных продуктов ГОСТ Р ИСО/МЭК 25010–2015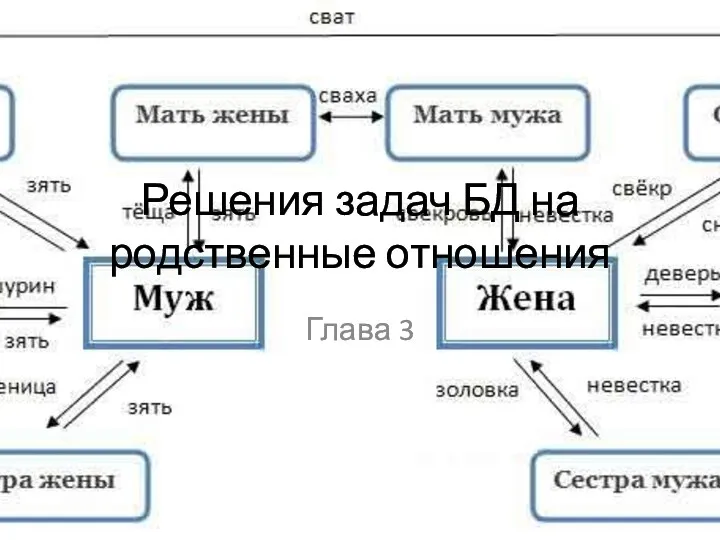 Базы данных. Решения задач на родственные отношения
Базы данных. Решения задач на родственные отношения Сайтов, помогающих при создании роликов и фильмов
Сайтов, помогающих при создании роликов и фильмов