Содержание
- 2. Поиск элементов массива с максимальным и минимальным значениями: • max(A) возвращает наибольший элемент, если A –
- 3. Например,max(A,[ ],1) возвращает максимальные элементы каждого столбца матрицы A; • [C,I] = max(A) – кроме максимальных
- 4. A = 30 39 48 1 10 19 28 38 47 7 9 18 27 29
- 5. >> C = max(A,[ ],2) C = 48 47 46 45 44 43 49 >> [C,I]
- 6. Сортировка элементов массива [s, i] = sort (x) [s, i] = sort (x, dim) [s, i]
- 7. V = -0.51301 -0.52824 -0.21580 -0.64126 0.14051 -0.57329 -0.42226 0.68796 -0.17928 0.36181 0.59941 -0.69113 -0.77139 0.32716
- 8. [s, i] = sortrows (A) [s, i] = sortrows (A, c) Сортировка строк, в соответствии с
- 9. Задание Решить задачу на собственные значения для матрицы Отсортировать собственные векторы в соответствии с собственными значениями,
- 10. Статистическая обработка данных Статистическая обработка данных, представляющих собой реализации случайных величин, заключается в вычислении таких характеристик
- 11. Математическое ожидание (среднее значение) mean (x) mean (x, dim) mean (x, opt) mean (x, dim, opt)
- 12. opt – определяет следующие выборы вычисления: “a” – среднее арифметическое (по умолчанию) “h” – среднее гармоническое
- 13. Медиана выборки median (x) median (x, dim) Для вычисления медианы нужно отсортировать массив Х (s=sort(X)). Тогда:
- 14. Стандартное и среднее квадратическое отклонения std (x) std (x, opt) std (x, opt, dim)
- 15. Коэффициент асимметрии распределений случайных величин skewness (x) skewness (x, flag) skewness (x, flag, dim) Асимметрия –
- 16. Коэффициент эксцесса распределения случайной величины kurtosis (x) kurtosis (x, flag) kurtosis (x, flag, dim) Эксцесс –
- 17. Квартили Предоставляют важную информацию о структуре вариационного ряда. Вместе с медианой они делят вариационный ряд на
- 18. statistics (x) statistics (x, dim) Для вектора Х возвращает следующие статистические характеристики: min(x), 1-й квартиль, медиану,
- 19. >> X=randn(1,10000); >> statistics (X) min 1 med 3 -3.5173146 -0.6750578 -0.0096442 0.6592135 max mean std
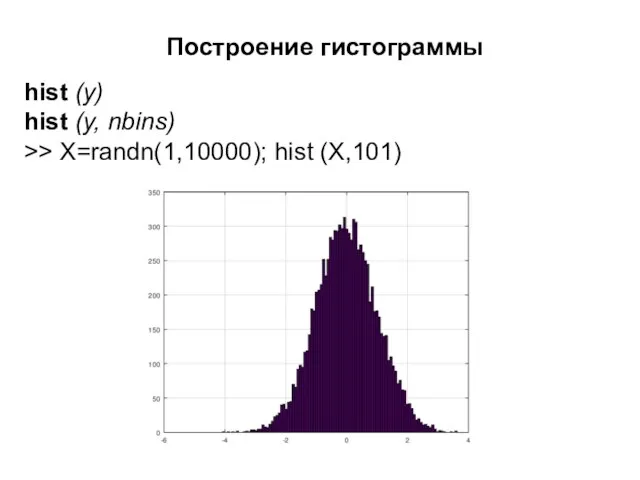
- 20. Построение гистограммы hist (y) hist (y, nbins) >> X=randn(1,10000); hist (X,101)
- 21. Дискретное преобразование Фурье В цифровой обработке сигналов широкое применение находит преобразование Фурье, которое сопоставляет каждой функции
- 22. fft (x) N – число елементов вектора x fft (x, n) N=n fft (x, n, dim)
- 23. Задание Найти преобразование Фурье сигнала, задаваемого соотношением: Выберите интервал дискретизации по времени dt, время наблюдения Т>2*tau,
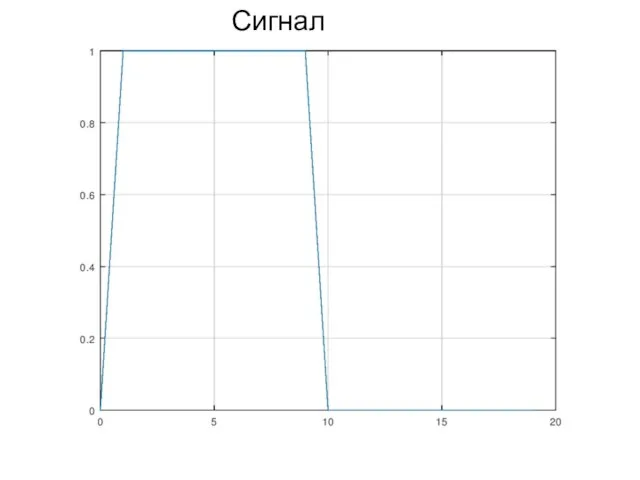
- 24. Сигнал
- 26. Скачать презентацию

![Например,max(A,[ ],1) возвращает максимальные элементы каждого столбца матрицы A; • [C,I] =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/853220/slide-2.jpg)

![>> C = max(A,[ ],2) C = 48 47 46 45 44](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/853220/slide-4.jpg)
![Сортировка элементов массива [s, i] = sort (x) [s, i] = sort](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/853220/slide-5.jpg)

![[s, i] = sortrows (A) [s, i] = sortrows (A, c) Сортировка](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/853220/slide-7.jpg)














 Машинное обучение
Машинное обучение Lektsia_1_Trendy_i_strategia
Lektsia_1_Trendy_i_strategia Kia how to электронная подпись
Kia how to электронная подпись Анализ реализации параметрической модели центробежного раскатника
Анализ реализации параметрической модели центробежного раскатника Новогодняя панорама Волшебное программирование
Новогодняя панорама Волшебное программирование Яндекс.Медицина
Яндекс.Медицина Списки литературы составление бланков данных
Списки литературы составление бланков данных Схемотехнический редактор и навигация
Схемотехнический редактор и навигация Золотое правило пирамиды Минто
Золотое правило пирамиды Минто Моделирование течений вязкой несжимаемой жидкости в системах конечно-элементного анализа
Моделирование течений вязкой несжимаемой жидкости в системах конечно-элементного анализа Сервис “Biteable” для создания анимированного видео
Сервис “Biteable” для создания анимированного видео Тахографы. История тахографов
Тахографы. История тахографов Массивы в С++
Массивы в С++ Середа О.А. ГПНТБ России. Бесконтактные библиотечные услуги (2)
Середа О.А. ГПНТБ России. Бесконтактные библиотечные услуги (2) Решение задач линейным симплекс-методом
Решение задач линейным симплекс-методом Арифметические команды. (Лекция 10)
Арифметические команды. (Лекция 10) Глобальная компьютерная сеть Интернет
Глобальная компьютерная сеть Интернет Алгоритмы. Основные элементы
Алгоритмы. Основные элементы Презентация на тему Ламповые Компьютеры
Презентация на тему Ламповые Компьютеры  РФ_Лаб_ООП_02
РФ_Лаб_ООП_02 Системы счисления. Деление (часть 8)
Системы счисления. Деление (часть 8) Создание собственной кисти в Photoshop
Создание собственной кисти в Photoshop Виды базы данных
Виды базы данных Творческие мастерские для медиаспециалиста
Творческие мастерские для медиаспециалиста Прикладные протоколы стека FTP и TFTP
Прикладные протоколы стека FTP и TFTP Что такое пиксель
Что такое пиксель Прикладное программное обеспечение
Прикладное программное обеспечение 2D-платформер. FairnSquare
2D-платформер. FairnSquare