Элементы алгебры логики

Ключевые слова
алгебра логики
высказывание
логическая операция
конъюнкция
дизъюнкция
отрицание
логическое выражение таблица истинности
законы логики

Клод Шеннон (1916-2001). Его исследования позволили применить алгебру логики в вычислительной технике
Логика
Аристотель (384-322 до н.э.). Основоположник формальной логики (понятие, суждение, умозаключение).
Джордж Буль (1815-1864). Создал новую область науки - Математическую логику (Булеву алгебру или Алгебру высказываний).

Алгебра - наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над разнообразными математическими объектами – числами, многочленами, векторами и др.
Алгебра

Высказывание - это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.
В русском языке высказывания выражаются повествовательными предложениями:
Земля вращается вокруг Солнца.
Москва - столица.
Побудительные и вопросительные предложения высказываниями не являются.
Без стука не входить!
Откройте учебники.
Ты выучил стихотворение?
Высказывание
Но не всякое повествовательное предложение является высказыванием:
Это высказывание ложное.

Высказывание или нет?
Зимой идет дождь.
Снегири живут в Крыму.
Кто к нам пришел?
У треугольника 5 сторон.
Как пройти в библиотеку?
Переведите число в десятичную систему.
Запишите домашнее задание

Алгебра логики определяет правила записи, вычисления значений, упрощения и преобразования высказываний.
В алгебре логики высказывания обозначают буквами и называют логическими переменными.
Если высказывание истинно, то значение соответствующей ему логической переменной обозначают единицей (А = 1), а если ложно - нулём (В = 0).
0 и 1 называются логическими значениями.
Алгебра логики

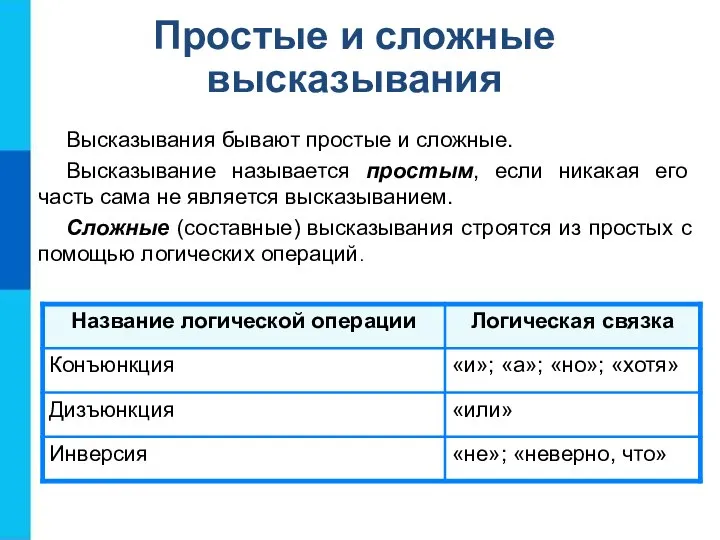
Простые и сложные высказывания
Высказывания бывают простые и сложные.
Высказывание называется простым, если никакая его часть сама не является высказыванием.
Сложные (составные) высказывания строятся из простых с помощью логических операций.

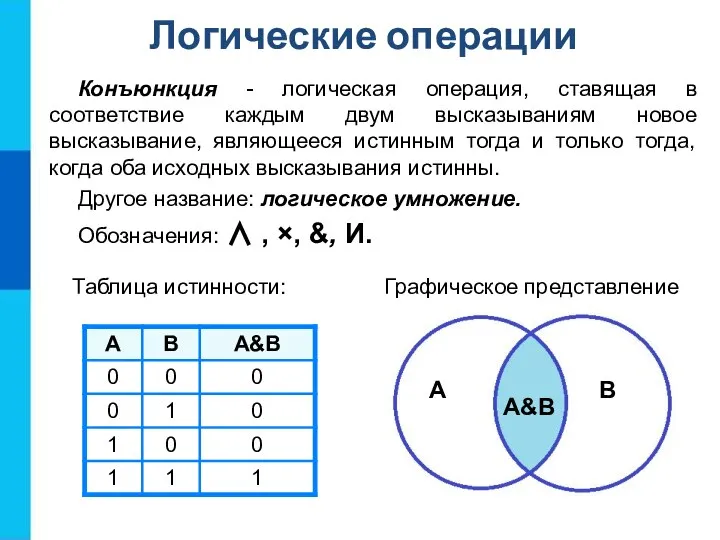
Конъюнкция - логическая операция, ставящая в соответствие каждым двум высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
Другое название: логическое умножение.
Обозначения: ∧ , ×, &, И.
Логические операции
Таблица истинности:
Графическое представление
A
B
А&В

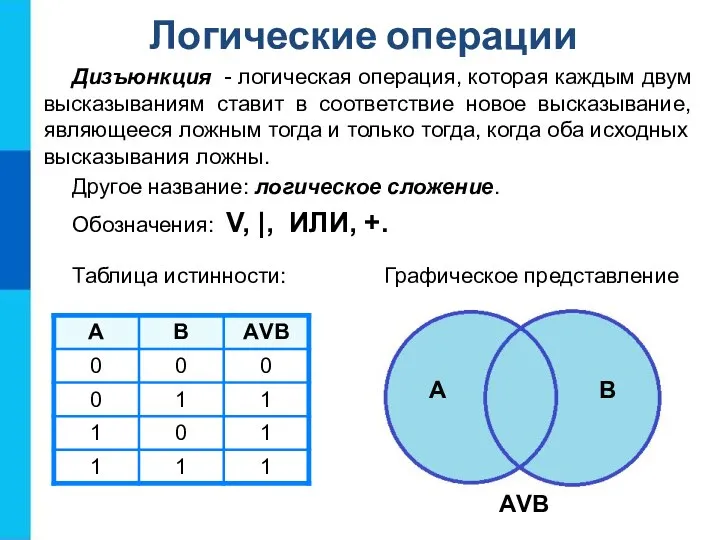
Дизъюнкция - логическая операция, которая каждым двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.
Другое название: логическое сложение.
Обозначения: V, |, ИЛИ, +.
Логические операции
Таблица истинности:
Графическое представление
A
B
АVВ

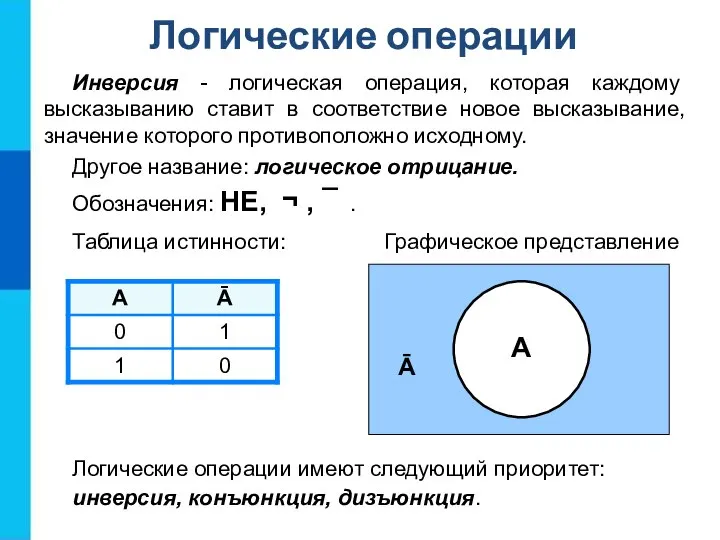
Инверсия - логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному.
Другое название: логическое отрицание.
Обозначения: НЕ, ¬ , ¯ .
Логические операции имеют следующий приоритет:
инверсия, конъюнкция, дизъюнкция.
Логические операции
Таблица истинности:
Графическое представление
A
Ā

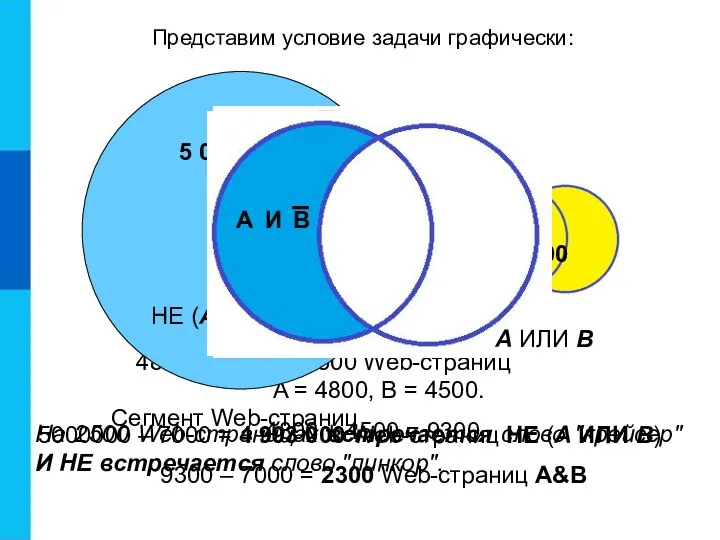
Пусть А = «На Web-странице встречается слово "крейсер"», В = «На Web-странице встречается слово "линкор"».
В некотором сегменте сети Интернет 5000000 Web-страниц. В нём высказывание А истинно для 4800 страниц, высказывание В - для 4500 страниц, а высказывание АVВ - для 7000 страниц.
Для какого количества Web-страниц в этом случае будут истинны следующие выражения и высказывание?
а) НЕ (А ИЛИ В);
б) А & B;
в) На Web-странице встречается слово "крейсер" И НЕ встречается слово "линкор".
Решаем задачу

5000000 – 7000 = 4 993 000 Web-страниц НЕ (А ИЛИ В) A = 4800, B = 4500.
4800 + 4500 = 9300
4800 – 2300 = 2500 Web-страниц
Представим условие задачи графически:
На 2500 Web-страницах встречается слово "крейсер" И НЕ встречается слово "линкор".
5 000 000
7 000
НЕ (А ИЛИ В)
Сегмент Web-страниц
A
B
A&B
9300 – 7000 = 2300 Web-страниц A&B
A
И
А ИЛИ В

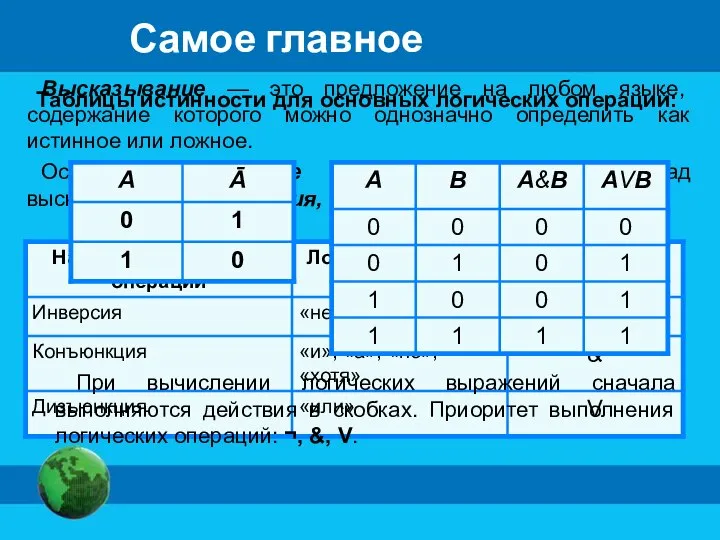
Высказывание — это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.
Основные логические операции, определённые над высказываниями: инверсия, конъюнкция, дизъюнкция.
Таблицы истинности для основных логических операций:
При вычислении логических выражений сначала выполняются действия в скобках. Приоритет выполнения логических операций: ¬, &, V.
Самое главное

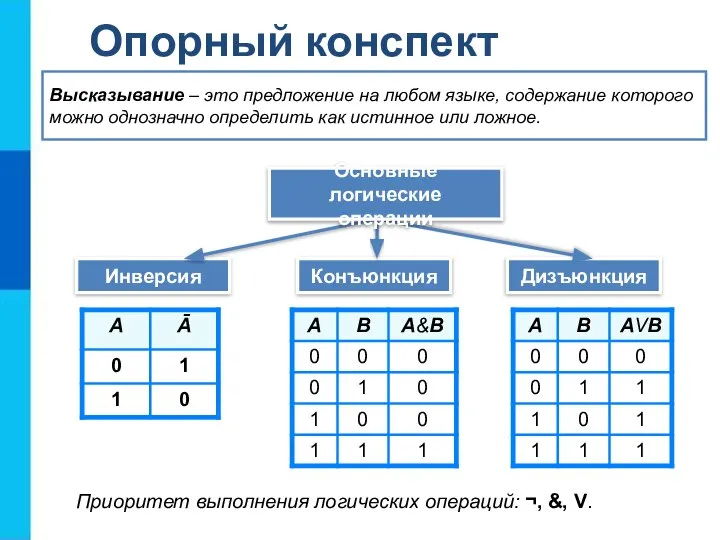
Опорный конспект
Инверсия
Конъюнкция
Дизъюнкция
Высказывание – это предложение на любом языке, содержание которого
можно однозначно определить как истинное или ложное.
Приоритет выполнения логических операций: ¬, &, V.
Основные логические
операции