Основы алгебры логики

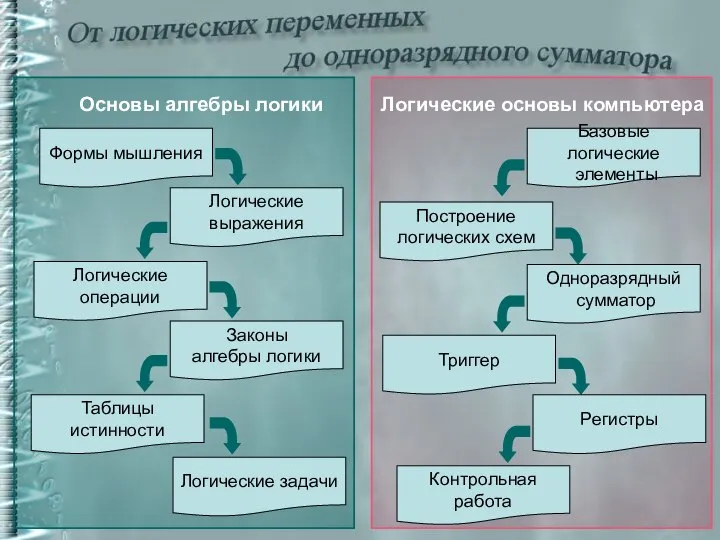
Формы мышления
Логические
выражения
Логические
операции
Законы
алгебры логики
Таблицы
истинности
Логические задачи
Основы алгебры логики
Логические основы компьютера
Базовые логические
элементы
Контрольная
работа
Построение
логических схем
Одноразрядный
сумматор
Триггер
Регистры

Формы мышления и история развития
алгебры логики
История логики насчитывает около двух с половиной тысячелетий. Первые учения о формах и способах мышления возникли в Древнем Китае и Индии. Основоположником формальной логики является Аристотель (384-322 гг. до н.э.) – древнегреческий философ, который впервые отделил логические формы мышления от его содержания.
Алгебра логики – наука об операциях, аналогичных математическим, над высказываниями или над объектами, которые могут принимать только два значения – «ИСТИНА» или «ЛОЖЬ».
В 1842 году английский математик Джорж Буль разработал математическую логику или алгебру логики, которую впоследствии стали называть «булевой алгеброй». Спустя 100 лет алгебра логики стала основой теории цифровых вычислительных машин, ее используют в компьютерной логике, электронике, в основе всех микропроцессорных операций.

Формы мышления и история развития
алгебры логики
Многие философы и математики развивали отдельные положения логики и иногда даже намечали контуры современного исчисления высказываний, но ближе всех к созданию математической логики подошел уже во второй половине XVII века выдающийся немецкий ученый Готфрид Вильгельм Лейбниц (1646— 1716), указавший пути для перевода логики “из словесного царства, полного неопределенностей, в царство математики, где отношения между объектами или высказываниями определяются совершенно точно”. Лейбниц надеялся даже, что в будущем философы, вместо того чтобы бесплодно спорить, станут брать бумагу и вычислять, кто из них прав. При этом в своих работах Лейбниц затрагивал и двоичную систему счисления.
Уже в XIX веке стало понятно, что система Буля хорошо подходит для описания электрических переключательных схем. Ток в цепи может либо протекать, либо отсутствовать, подобно тому, как утверждение может быть либо истинным, либо ложным. А еще несколько десятилетий спустя, уже в XX столетии, ученые объединили созданный Джорджем Булем математический аппарат с двоичной системой счисления, заложив тем самым основы для разработки цифрового электронного компьютера.

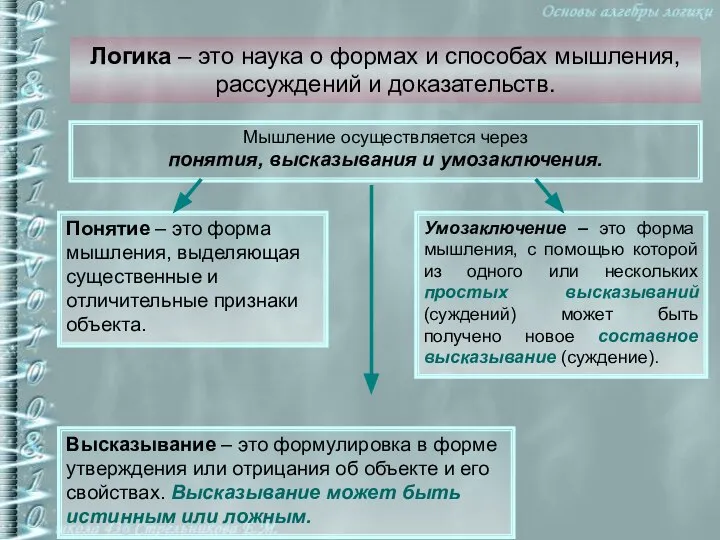
Логика – это наука о формах и способах мышления, рассуждений и доказательств.
Мышление осуществляется через
понятия, высказывания и умозаключения.
Понятие – это форма мышления, выделяющая существенные и отличительные признаки объекта.
Высказывание – это формулировка в форме утверждения или отрицания об объекте и его свойствах. Высказывание может быть истинным или ложным.
Умозаключение – это форма мышления, с помощью которой из одного или нескольких простых высказываний (суждений) может быть получено новое составное высказывание (суждение).
0

Примеры высказываний
Истинное высказывание: «Буква «А» - гласная».
Ложное высказывание: «Компьютер был изобретен в середине XIX века».
Какие из предложений являются высказываниями? Какие из высказываний истинные?
1. Какой длины эта лента?
2. Прослушайте сообщение.
3. Делайте утреннюю зарядку!
4. Назовите устройства ввода информации.
5. Кто отсутствует?
6. Париж – столица Англии.
7. Число 11 является простым.
8. 4+5=10
9. Без труда не вытащишь и рыбку из пруда.
10. Сложите числа 2 и 5.
11. Некоторые медведи живут на Севере.
12. Все медведи – бурые.
13. Чему равно расстояние от Москвы до Ленинграда?
14. Сумма углов треугольника – 180 градусов.
0

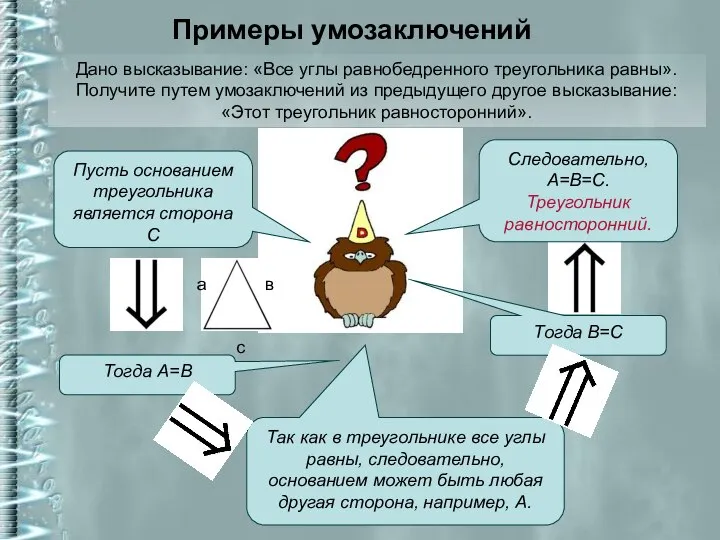
Примеры умозаключений
Дано высказывание: «Все углы равнобедренного треугольника равны». Получите путем умозаключений из предыдущего другое высказывание: «Этот треугольник равносторонний».
Тогда А=В
Так как в треугольнике все углы равны, следовательно, основанием может быть любая другая сторона, например, А.
Тогда В=С
Следовательно, А=В=С. Треугольник равносторонний.
Пусть основанием треугольника является сторона С

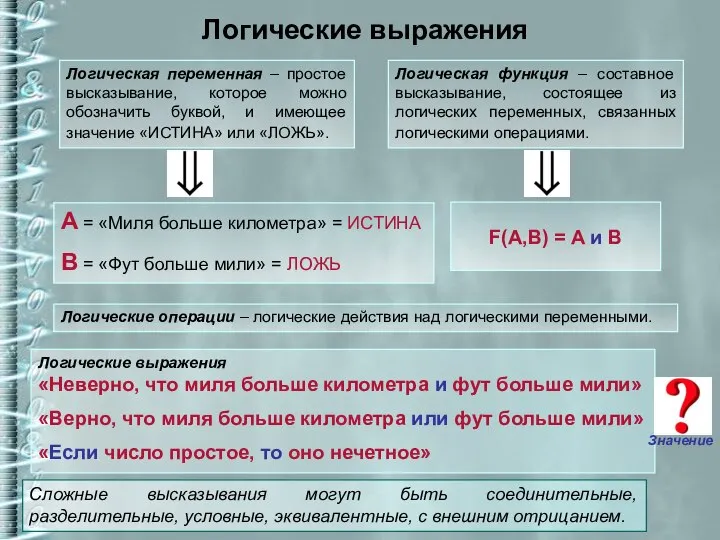
Логические выражения
Логическая переменная – простое высказывание, которое можно обозначить буквой, и имеющее значение «ИСТИНА» или «ЛОЖЬ».
Логическая функция – составное высказывание, состоящее из логических переменных, связанных логическими операциями.
Логические операции – логические действия над логическими переменными.
А = «Миля больше километра» = ИСТИНА
В = «Фут больше мили» = ЛОЖЬ
F(A,B) = A и В
Логические выражения
«Неверно, что миля больше километра и фут больше мили»
«Верно, что миля больше километра или фут больше мили»
«Если число простое, то оно нечетное»
Сложные высказывания могут быть соединительные, разделительные, условные, эквивалентные, с внешним отрицанием.
Значение

Логические операции
Каждое составное высказывание можно выразить в виде формулы (логического выражения), в которую войдут логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции.
ИСТИНА – 1
ЛОЖЬ - 0
Таблица истинности определяет значение сложного высказывания при всех возможных значениях простых высказываний

Инверсия - логическое отрицание
От лат. inversio - переворачиваю
Логическое отрицание делает истинное высказывание ложным и, наоборот, ложное – истинным.
Таблица истинности функции логического отрицания
Пример: Даны высказывания
А – «Число 10 – четное» = ИСТИНА
В – «Число 10 – отрицательное» = ЛОЖЬ
С – «Луна – спутник Земли» = ИСТИНА
Не А – «Неверно, что число 10 – четное» = ЛОЖЬ
Не В – «Неверно, что число 10 – отрицательное» = ИСТИНА
Не С – «Неверно, что Луна – спутник Земли» = ЛОЖЬ
В переводе на естественный язык
«Не А»
«Неверно, что А»
ИСТИНА – 1
ЛОЖЬ - 0
0

Конъюнкция - логическое умножение
От лат. conjunctio - связываю
Результат логического умножения является истинным тогда и только тогда, когда истинны все входящие в него простые высказывания.
Таблица истинности функции логического умножения
В переводе на естественный язык
«и А, и В» «как А, так и В»
«А вместе с В» «А несмотря на В»
«А, в то время как В»
И , , and, &, *, ·
Пример: Даны высказывания
А – «Число 10 – четное» = ИСТИНА
В – «Число 10 – отрицательное» = ЛОЖЬ
С – «Число 10 кратно 2» = ИСТИНА
А и В – «Число 10 – четное и отрицательное» - ЛОЖЬ
А и С – «Число 10 как четное, так и кратно 2» - ИСТИНА
0

Дизъюнкция - логическое сложение
От лат. disjunctio – различаю
Результат логического сложения является истинным тогда, когда истинно хотя бы одно из входящих в него простых высказываний.
В переводе на естественный язык
«А или В»
Таблица истинности функции логического сложения
Пример: Даны высказывания
А – «Число 10 – четное» = ИСТИНА
В – «Число 10 – отрицательное» = ЛОЖЬ
С – «Число 10 - простое» = ЛОЖЬ
А или В – «Число 10 – четное или отрицательное» ИСТИНА
А или С – «Число 10 четное или простое» - ИСТИНА
В или С – «Число 10 отрицательное или простое» - ЛОЖЬ
ИЛИ, , or, +
0

Эквивалентность - логическое равенство
Результат логического равенства является истинным тогда и только тогда, когда оба высказывания одновременно либо истинны, либо ложны.
От лат. aeguivalens – равноценное
Таблица истинности функции логического равенства
В переводе на естественный язык
«А эквивалентно В» «А тогда и только тогда, когда В»
=,
Пример: Даны высказывания
А – «Число 10 – четное» = ИСТИНА
В – «Число 10 – отрицательное» = ЛОЖЬ
С – «Число 10 - простое» = ЛОЖЬ
А В – «Число 10 – четное, тогда и только тогда, когда оно - отрицательное» - ЛОЖЬ
В С – «Число 10 такое же простое, как и отрицательное» ИСТИНА
0

Неравнозначность (исключающее ИЛИ)
Результат неравнозначности является истинным тогда, когда является истинным либо один ее аргумент, либо другой, но не оба вместе.
В переводе на естественный язык
«А или В, но не оба», «А либо В», «либо А, либо В», «либо не А, либо не В», «или А, или В», «только А или только В»
Таблица истинности функции неравнозначности
Пример: Даны высказывания
А – «Студент получил двойку» = ЛОЖЬ
В – «Студент получил тройку» = ИСТИНА
С – «Студент сдал экзамен» = ИСТИНА
или А, или В – «Студент получил или двойку, или тройку» ИСТИНА
или В, или С – «Студент или получил тройку, или сдал экзамен» ЛОЖЬ
XOR, ⊕
0

Импликация - логическое следование
Результат логического следования является ложным тогда и только тогда, когда из истины следует ложь.
От лат. implicatio – тесно связывать
Таблица истинности функции логического следования
А – условие, В - следствие
В переводе на естественный язык
«если А, то В» «В, если А»
«Когда А, тогда и В»
«А достаточно для В»
«А только тогда, когда В»
Пример: Даны высказывания
А – «Число 10 – четное» = ИСТИНА
В – «Число 10 – отрицательное» = ЛОЖЬ
С – «Число 10 - простое» = ЛОЖЬ
А В – «Если число 10 – четное,
то оно - отрицательное» - ЛОЖЬ
А С – «Число 10 простое, если четное» - ЛОЖЬ
«Если число делится на 10, то оно делится на 5» ИСТИНА
0

«Точка Х принадлежит интервалу [A;B]»
Примеры записи высказываний в виде логических выражений
«Летом Петя поедет в деревню и, если будет хорошая погода, то он будет рыбачить.»
1
А
В
С
При составлении логического выражения необходимо учитывать порядок выполнения логических операций:
действия в скобках
инверсия
конъюнкция
дизъюнкция
неравнозначность
эквивалентность
импликация
.
F=A * (B C)
2
(X>=A) * (X<=B)
«Точка Х не принадлежит интервалу [A;B]»
3
(X>=A) * (X<=B)
(X
B)
«Неверно, что если дует ветер, то солнце светит только тогда, когда нет дождя.»
4
В
С
D – идет дождь
В (D C)
0

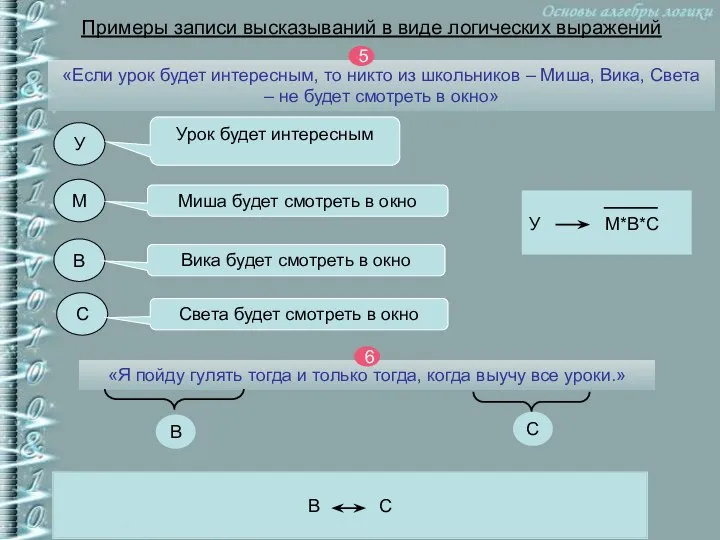
В С
Примеры записи высказываний в виде логических выражений
«Если урок будет интересным, то никто из школьников – Миша, Вика, Света – не будет смотреть в окно»
5
У
М
В
С
Урок будет интересным
Миша будет смотреть в окно
Вика будет смотреть в окно
Света будет смотреть в окно
У М*В*С
«Я пойду гулять тогда и только тогда, когда выучу все уроки.»
6
В
С
0

Упражнения c логическими выражениями
По мишеням произведено три выстрела. Рассмотрено высказывание:
Pk = «Мишень поражена к-тым выстрелом», где к=1, 2, 3.
Что означают следующие высказывания:
а) P1 + P2 + P3 б) P1 * P2 * P3 в)P1 * P2 * P3
7
Построить таблицу истинности для выражения F=(A+B)*(A+B)
8
Вычислить значение булевского выражения X1*X2+X3+X4, при X1=1, X2=0, X3=1, X4=0.
9
1*0 + 1 + 0 = 1*0 +0 +1 = 0 + 0 + 1= 1

ГБОУ школа №430 Стрельникова Е.М
Законы алгебры логики
A B = A+B
A B =( A+B)*(B+A)
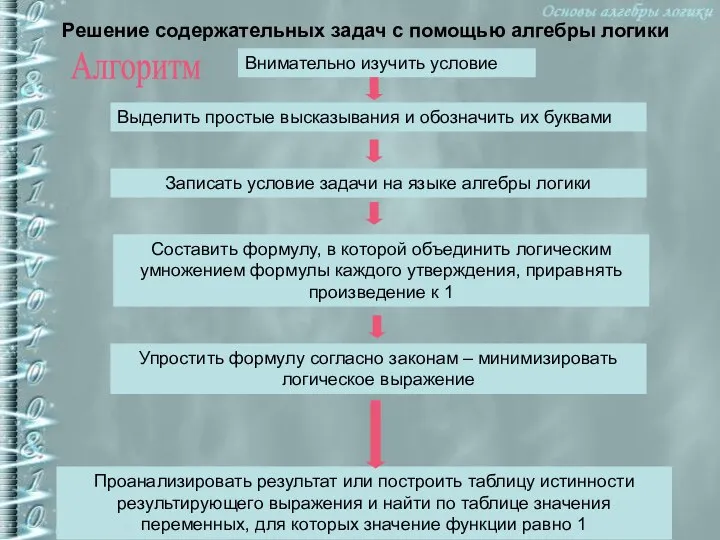
0

Решение содержательных задач с помощью алгебры логики
Алгоритм
Внимательно изучить условие
Выделить простые высказывания и обозначить их буквами
Записать условие задачи на языке алгебры логики
Составить формулу, в которой объединить логическим умножением формулы каждого утверждения, приравнять произведение к 1
Упростить формулу согласно законам – минимизировать логическое выражение
Проанализировать результат или построить таблицу истинности результирующего выражения и найти по таблице значения переменных, для которых значение функции равно 1
0

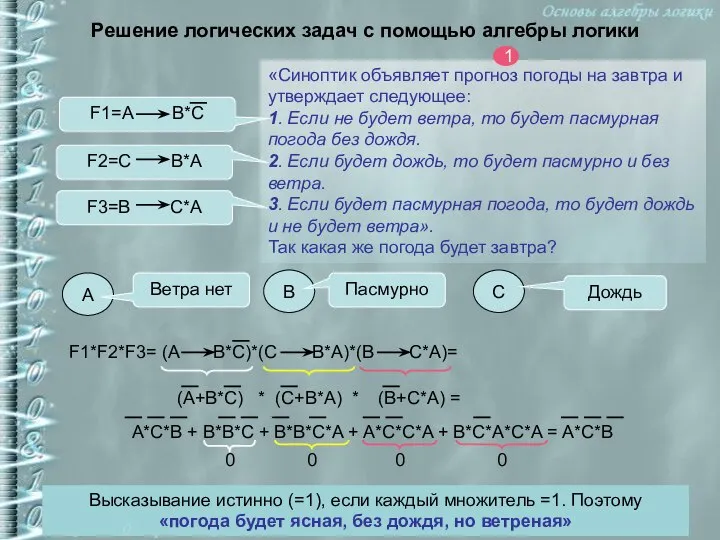
Решение логических задач с помощью алгебры логики
«Синоптик объявляет прогноз погоды на завтра и утверждает следующее:
1. Если не будет ветра, то будет пасмурная погода без дождя.
2. Если будет дождь, то будет пасмурно и без ветра.
3. Если будет пасмурная погода, то будет дождь и не будет ветра».
Так какая же погода будет завтра?
1
А
В
С
Ветра нет
Пасмурно
Дождь
F1=A B*C
F2=C B*A
F3=B C*A
F1*F2*F3= (A B*C)*(C B*A)*(B C*A)=
(A+B*C) * (C+B*A) * (B+C*A) =
A*C*B + B*B*C + B*B*C*A + A*C*C*A + B*C*A*C*A = A*C*B
0
0
0
0
Высказывание истинно (=1), если каждый множитель =1. Поэтому
«погода будет ясная, без дождя, но ветреная»
0

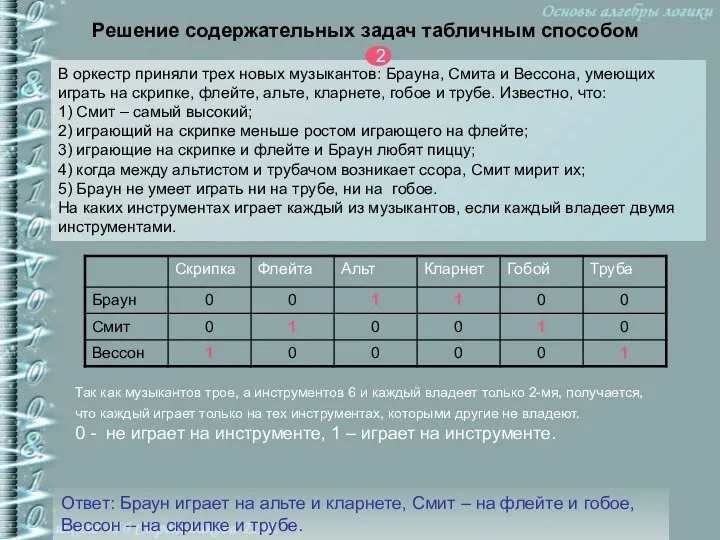
Решение содержательных задач табличным способом
В оркестр приняли трех новых музыкантов: Брауна, Смита и Вессона, умеющих играть на скрипке, флейте, альте, кларнете, гобое и трубе. Известно, что:
1) Смит – самый высокий;
2) играющий на скрипке меньше ростом играющего на флейте;
3) играющие на скрипке и флейте и Браун любят пиццу;
4) когда между альтистом и трубачом возникает ссора, Смит мирит их;
5) Браун не умеет играть ни на трубе, ни на гобое.
На каких инструментах играет каждый из музыкантов, если каждый владеет двумя инструментами.
Так как музыкантов трое, а инструментов 6 и каждый владеет только 2-мя, получается, что каждый играет только на тех инструментах, которыми другие не владеют.
0 - не играет на инструменте, 1 – играет на инструменте.
Ответ: Браун играет на альте и кларнете, Смит – на флейте и гобое, Вессон – на скрипке и трубе.
2
0

Решение содержательных задач с помощью рассуждений
Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский и арабский. На вопрос, какой язык изучает каждый из них, один ответил: «Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский». Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый?
Решение.
Если верно первое утверждение, то верно и второе, так как юноши изучают разные языки. Это противоречит условию задачи, поэтому первое утверждение ложно.
Если верно второе утверждение, то первое и третье должны быть ложны. При этом получается, что никто не изучает китайский. Это противоречит условию, поэтому второе утверждение тоже ложно.
Остается считать верным третье утверждение, а первое и второе – ложными. Следовательно, Вадим не изучает китайский, китайский изучает Сергей.
Ответ: Сергей изучает китайский язык, Михаил – японский, Вадим – арабский.
3
0