Основы программирования на Java

Целочисленные алгоритмы
Тема 1. Алгоритм Евклида

Вычисление НОД
НОД = наибольший общий делитель двух натуральных чисел – это наибольшее число, на которое оба исходных числа делятся без остатка.
Перебор:
k = a; // или k = b;
while ( a % k != 0 ||
b % k != 0 )
k --;
printf ("НОД(%d,%d)=%d", a, b, k);
много операций для больших чисел
ИЛИ

Алгоритм Евклида
Евклид
(365-300 до. н. э.)
НОД(a,b)= НОД(a-b, b)
= НОД(a, b-a)
Заменяем большее из двух чисел разностью большего и меньшего до тех пор, пока они не станут равны. Это и есть НОД.
НОД (14, 21) = НОД (14, 21-14) = НОД (14, 7)
НОД (1998, 2) = НОД (1996, 2) = … = 2
Пример:
много шагов при большой разнице чисел:
= НОД (7, 7) = 7

Модифицированный алгоритм Евклида
НОД(a,b)= НОД(a%b, b)
= НОД(a, b%a)
Заменяем большее из двух чисел остатком от деления большего на меньшее до тех пор, пока меньшее не станет равно нулю. Тогда большее — это НОД.
НОД (14, 21) = НОД (14, 7) = НОД (0, 7) = 7
Пример:
Еще один вариант:
НОД(2·a,2·b)= 2·НОД(a, b)
НОД(2·a,b)= НОД(a, b) // при нечетном b

Реализация алгоритма Евклида
Рекурсивный вариант:
Без рекурсии:
static int gcd(int a,int b)
{
if ( a == b ) return a;
if ( a < b )
return gcd ( a, b-a );
else return gcd ( a-b, b );
}
static int gcd(int a, int b)
{
while ( a != b )
if ( a > b ) a -= b;
else b -= a;
return a;
}
static int gcd(int a,int b)
{
if ( a*b == 0 ) return a + b;
if ( a < b )
return gcd ( a, b%a );
else return gcd ( a%b, b );
}
static int gcd(int a, int b)
{
while ( a*b != 0 )
if ( a > b ) a = a % b;
else b = b % a;
return a + b;
}

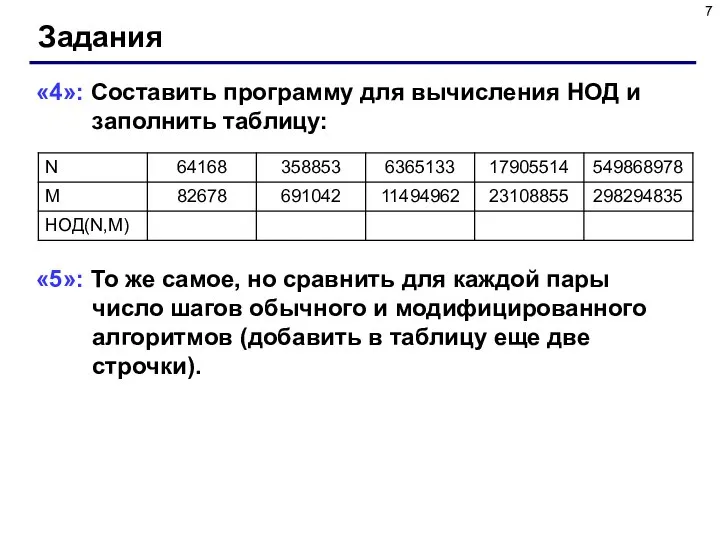
Задания
«4»: Составить программу для вычисления НОД и заполнить таблицу:
«5»: То же самое, но сравнить для каждой пары число шагов обычного и модифицированного алгоритмов (добавить в таблицу еще две строчки).

Целочисленные алгоритмы
Тема 2. Решето Эратосфена

Поиск простых чисел
Простые числа – это числа, которые делятся только на себя и на 1.
Применение:
криптография;
генераторы псевдослучайных чисел.
Наибольшее известное (26 декабря 2017):
277 232 917 − 1 (содержит 23 249 425 цифр).
Задача. Найти все простые числа в интервале от 1 до заданного N.
Простое решение:
for ( i = 1; i <= N; i++ ) {
isPrime = true;
for ( k = 2; k < i ; k++ )
if ( i % k == 0 ) {
isPrime = false; break;
}
if ( isPrime ) printf("%d\n", i);
}
k*k <= i
k*k <= i
O(N2)
растет не быстрее N2

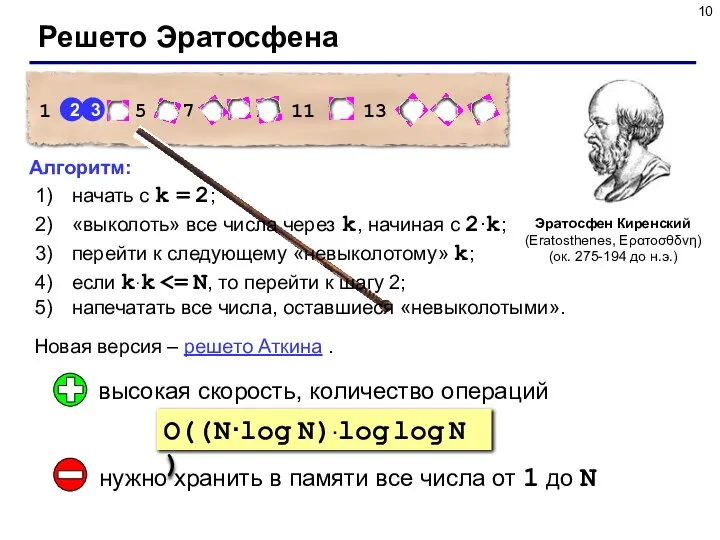
Решето Эратосфена
Эратосфен Киренский
(Eratosthenes, Ερατοσθδνη)
(ок. 275-194 до н.э.)
Новая версия – решето Аткина .
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Алгоритм:
начать с k = 2;
«выколоть» все числа через k, начиная с 2·k;
перейти к следующему «невыколотому» k;
если k·k <= N, то перейти к шагу 2;
напечатать все числа, оставшиеся «невыколотыми».
высокая скорость, количество операций
нужно хранить в памяти все числа от 1 до N
O((N·log N)·log log N )
2
3

Реализация
// сначала все числа не выколоты
for ( i = 1; i <= N; i ++ )
A[i] = true;
// основной цикл
for ( k = 2; k*k <= N; k ++ )
if ( A[k])
for ( i = k+k; i <= N; i += k ) A[i] = false;
// выводим оставшиеся числа
for ( i = 1; i <= N; i ++ )
if ( A[i])
printf ( "%d\n", i );
Массив A[N+1], где A[i]=true, если число i не «выколото», A[i]=false, если число i «выколото».

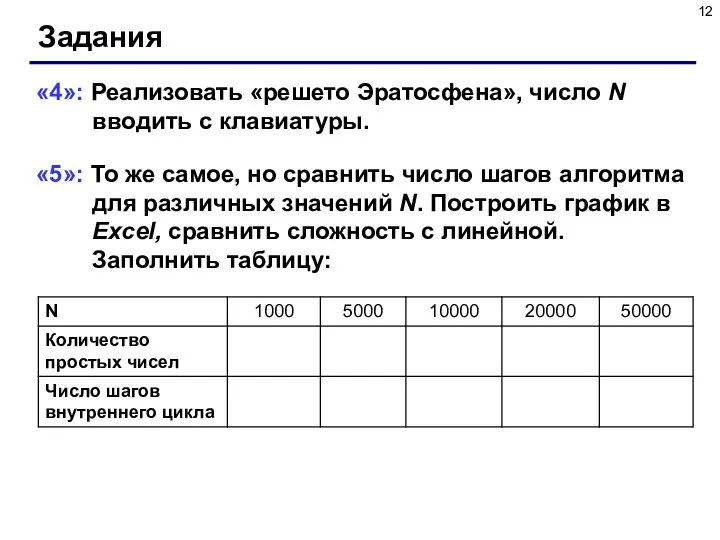
Задания
«4»: Реализовать «решето Эратосфена», число N вводить с клавиатуры.
«5»: То же самое, но сравнить число шагов алгоритма для различных значений N. Построить график в Excel, сравнить сложность с линейной. Заполнить таблицу:

Целочисленные алгоритмы
Тема 3. Длинные числа

Что такое длинные числа?
Задача. Вычислить (точно)
100! = 1·2·3·...·99·100
Проблема:
это число содержит более 100 цифр…
Решение:
хранить цифры в виде массива, по группам (например, 6 цифр в ячейке).
100! < 100100
201 цифра
201/6 ≈ 34 ячейки

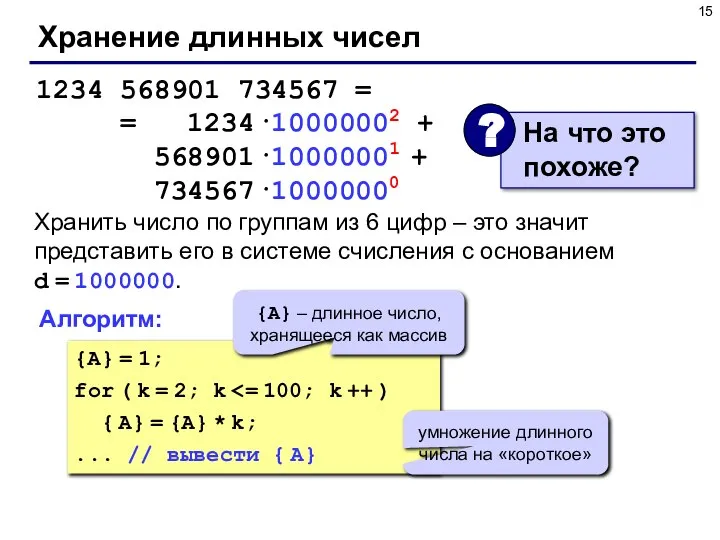
Хранение длинных чисел
1234 568901 734567 =
= 1234·10000002 +
568901·10000001 +
734567·10000000
Хранить число по группам из 6 цифр – это значит представить его в системе счисления с основанием
d = 1000000.
{A} = 1;
for ( k = 2; k <= 100; k ++ )
{ A} = {A} * k;
... // вывести { A}
Алгоритм:
{A} – длинное число, хранящееся как массив
умножение длинного числа на «короткое»

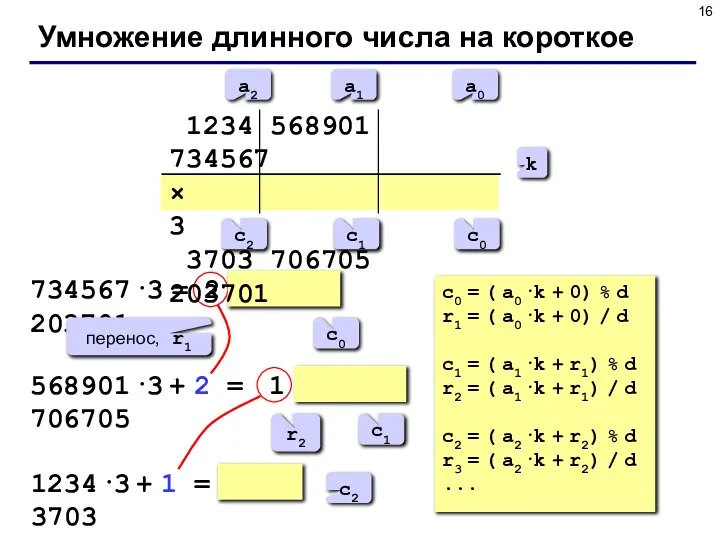
Умножение длинного числа на короткое
1234 568901 734567
× 3
3703 706705 203701
k
a0
a1
a2
c0
c1
c2
734567·3 = 2 203701
c0
перенос, r1
568901·3 + 2 = 1 706705
c1
r2
1234·3 + 1 = 3703
c2
c0 = ( a0·k + 0) % d
r1 = ( a0·k + 0) / d
c1 = ( a1·k + r1) % d
r2 = ( a1·k + r1) / d
c2 = ( a2·k + r2) % d
r3 = ( a2·k + r2) / d
...

Вычисление 100!
int d = 1000000; // основание системы
int s, r; // произведение, остаток
int[] A = new int[40];
A[0] = 1; // A[0]=1, остальные A[i]=0
int i, k, len = 1; // len – длина числа
for ( k = 2; k <= 100; k ++ ) {
i = 0;
r = 0;
while ( i < len || r > 0 ) {
s = A[i]*k + r;
A[i] = s % d; // остается в этом разряде
r = s / d; // перенос
i ++;
}
len = i; // новая длина числа
}
пока не кончились цифры числа {A} или есть перенос