Содержание
- 2. У Г А Т У Содержание лекции Уфимский государственный авиационный технический университет Базовые операции Побитное сложение
- 3. У Г А Т У Побитное сложение по модулю 2 Уфимский государственный авиационный технический университет Для
- 4. У Г А Т У Арифметические операции Уфимский государственный авиационный технический университет Применяются сложение (a +
- 5. У Г А Т У Перестановка [permutation] Уфимский государственный авиационный технический университет Биты меняются местами Количество
- 6. У Г А Т У Перестановка [permutation] Уфимский государственный авиационный технический университет
- 7. У Г А Т У Подстановка [substitution] Уфимский государственный авиационный технический университет Замена блока бит на
- 8. У Г А Т У Подстановка [substitution] Уфимский государственный авиационный технический университет Программная реализация: Таблица замен
- 9. У Г А Т У Подстановки и перестановки Уфимский государственный авиационный технический университет Существуют подобные операции,
- 10. У Г А Т У Дополнение [padding] Уфимский государственный авиационный технический университет Алгоритмы часто оперируют блоками
- 11. У Г А Т У Содержание лекции Уфимский государственный авиационный технический университет Базовые операции Способы построения
- 12. У Г А Т У Способы построения алгоритмов Уфимский государственный авиационный технический университет Симметричные алгоритмы бывают
- 13. У Г А Т У Гаммирование Уфимский государственный авиационный технический университет Основной способ построения поточных алгоритмов
- 14. У Г А Т У Подстановочно-перестановочная сеть Уфимский государственный авиационный технический университет SP-сеть Способ построения блочных
- 15. У Г А Т У Сеть Фейстеля Уфимский государственный авиационный технический университет Сбалансированная Способ построения блочных
- 16. У Г А Т У Сеть Фейстеля Уфимский государственный авиационный технический университет Сбалансированная При расшифровывании выполняются
- 17. У Г А Т У Блочные алгоритмы Уфимский государственный авиационный технический университет Сравнение SP-cети с сетью
- 18. У Г А Т У Содержание лекции Уфимский государственный авиационный технический университет Базовые операции Способы построения
- 19. У Г А Т У Режимы блочного шифрования Уфимский государственный авиационный технический университет Блочный алгоритм задает
- 20. У Г А Т У Режим ECB Уфимский государственный авиационный технический университет ECB CBC
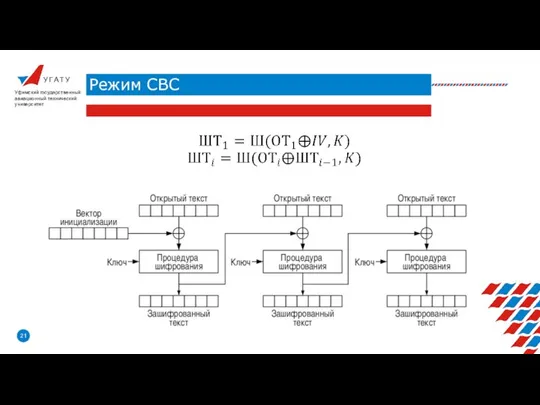
- 21. У Г А Т У Режим CBС Уфимский государственный авиационный технический университет
- 22. У Г А Т У Режим CBС Уфимский государственный авиационный технический университет
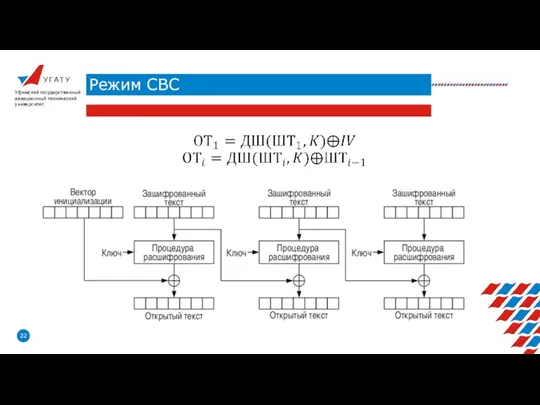
- 23. У Г А Т У Режим CBС Уфимский государственный авиационный технический университет Режим зацепления блоков шифротекста
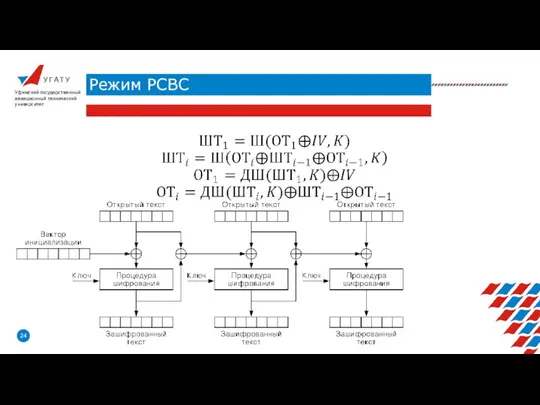
- 24. У Г А Т У Режим PCBС Уфимский государственный авиационный технический университет
- 25. У Г А Т У Режим PCBС Уфимский государственный авиационный технический университет
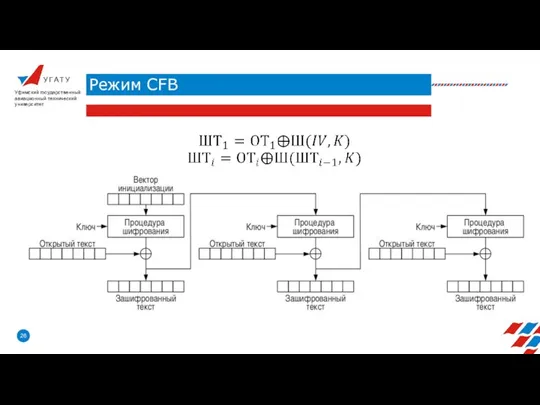
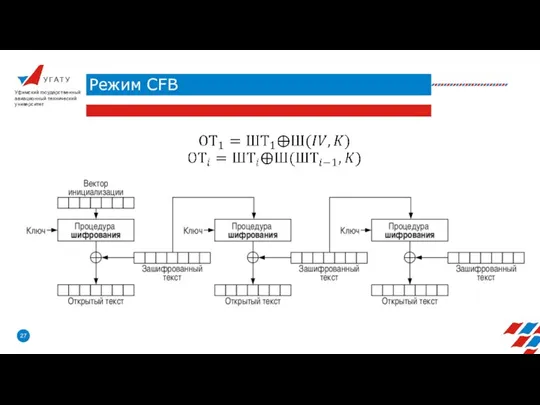
- 26. У Г А Т У Режим CFB Уфимский государственный авиационный технический университет
- 27. У Г А Т У Режим CFB Уфимский государственный авиационный технический университет
- 28. У Г А Т У Режим CFB Уфимский государственный авиационный технический университет Режим гаммирования с обратной
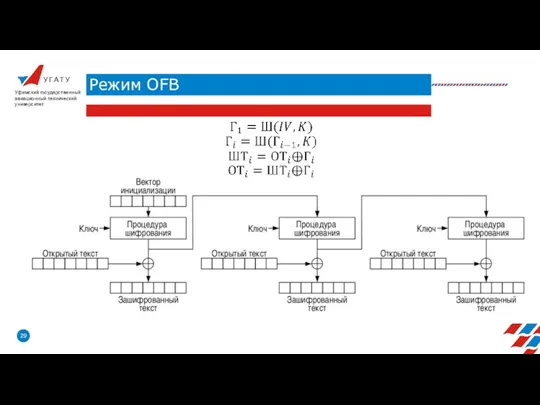
- 29. У Г А Т У Режим OFB Уфимский государственный авиационный технический университет
- 30. У Г А Т У Режим OFB Уфимский государственный авиационный технический университет Режим обратной связи по
- 31. У Г А Т У Режим CTR Уфимский государственный авиационный технический университет * Здесь и далее
- 33. Скачать презентацию



![У Г А Т У Перестановка [permutation] Уфимский государственный авиационный технический университет](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1043926/slide-4.jpg)
![У Г А Т У Перестановка [permutation] Уфимский государственный авиационный технический университет](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1043926/slide-5.jpg)
![У Г А Т У Подстановка [substitution] Уфимский государственный авиационный технический университет](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1043926/slide-6.jpg)
![У Г А Т У Подстановка [substitution] Уфимский государственный авиационный технический университет](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1043926/slide-7.jpg)

![У Г А Т У Дополнение [padding] Уфимский государственный авиационный технический университет](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1043926/slide-9.jpg)















 Применение информационных технологий в фармацевтической деятельности
Применение информационных технологий в фармацевтической деятельности Инструкция по установке программного обеспечения ArTecрвом веке
Инструкция по установке программного обеспечения ArTecрвом веке База данных SQLite. Лекция 12
База данных SQLite. Лекция 12 Как обогнать Директ и instagram при помощи Google Adwords
Как обогнать Директ и instagram при помощи Google Adwords Переменные. Типы данных С++
Переменные. Типы данных С++ Некоторые понятия, связанные с ЭС и ИИ
Некоторые понятия, связанные с ЭС и ИИ Maths. Switcher
Maths. Switcher Элементы алгебры, логики. Математические основы информатики
Элементы алгебры, логики. Математические основы информатики Алгоритмы цветового кодирования для повышения информативности компьютерных визуализаций
Алгоритмы цветового кодирования для повышения информативности компьютерных визуализаций Тестирование. Начало
Тестирование. Начало Что такое массив?
Что такое массив? 5 2 ИОННАЯ ИМПЛАНТАЦИЯ
5 2 ИОННАЯ ИМПЛАНТАЦИЯ Вопросы по онлайн оформлению груза в личном кабинете
Вопросы по онлайн оформлению груза в личном кабинете Obraz Rosji w polskich mediach
Obraz Rosji w polskich mediach Инструменты для принятия входящих звонков и совершения исходящих звонков
Инструменты для принятия входящих звонков и совершения исходящих звонков Информатика
Информатика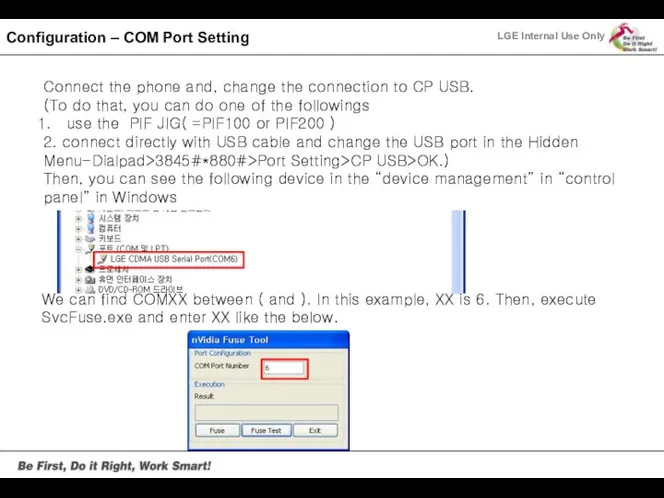 Configuration – COM Port Setting
Configuration – COM Port Setting Программный продукт Система формирования отчетности
Программный продукт Система формирования отчетности Знакомство с каскадными таблицами стилей
Знакомство с каскадными таблицами стилей Подразделение в документах движения ДС
Подразделение в документах движения ДС Текстовый редактор Word. Вставка графических объектов в текстовый документ
Текстовый редактор Word. Вставка графических объектов в текстовый документ Операторы PHP
Операторы PHP Операции импликация и эквивалентность
Операции импликация и эквивалентность Практика. Курсовой проект. Страница интернет магазина
Практика. Курсовой проект. Страница интернет магазина Домашнее задание. Подготовка электронной презентации по одному из художников XIX века
Домашнее задание. Подготовка электронной презентации по одному из художников XIX века Инструкция по обновлению GN2020
Инструкция по обновлению GN2020 Метрики в задачах ранжирования и матчинга
Метрики в задачах ранжирования и матчинга Презентация на тему Визуальная среда Delphi
Презентация на тему Визуальная среда Delphi